（論文）Multi-task Deep Reinforcement Learning with PopArt（2018）

Source

• Multi-task Deep Reinforcement Learning with PopArt
• Learning values across many orders of magnitude
• IMPALA: Scalable Distributed Deep-RL with Importance Weighted Actor-Learner Architectures
• Preserving Outputs Precisely while Adaptively Rescaling Targets
• Reinforcement Learning with Unsupervised Auxiliary Tasks
• What’s New in Deep Learning Research: How DeepMind Builds Multi-Task Reinforcement Learning Algorithms That Don’t Get Distracted

Introduction

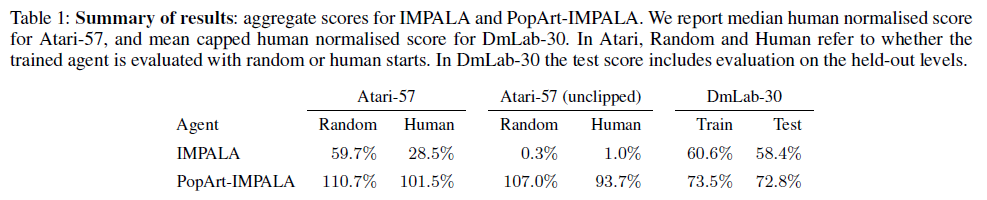
There have been numerous successful cases where a reinforcement agent being able to perform at super human level at various games. However, while the agent retains the same network structure throughout, it needs to be expertly trained on the specific game they are currently trying to conquer. Despite the progress DeepMind has made with IMPALA, where the aim is to create an agent that can multi-task, the final performance can only achieve a 59.7% median human normalized score across 57 Atari games, and a 49.4% mean human normalized score across 30 DeepMind Lab levels (DmLab-30).

One particular reason is that different games has a different rewarding system, causing the agent to tunnel-vision on tasks that yield higher rewards. For example, if game A can only provided a maximum reward of +1 at each step, whereas game B offers +1000, it is without question that the model will be more inclined to solve for game B due to saliency.

To alleviate this issue, a method named PopArt was proposed, where the rewards in each game are scaled so that each game becomes of equal learning value. With the collaboration between PopArt and IMPALA, a single agent is now capable of playing 57 Atari games with above-human median performance (110% median human normalized) and 72.8% mean human normalized score on DmLab-30.

Implementation

The goal is to have a single agent to learn N different environments . This can be formalised as a single large MDP whose state space is where i is the task index. The task index is only used at training time, not during testing.

The agent is an actor-critic that utilizes deep neural network for both its policy and value network. The policy is updated using REINFORCE algorithm
.
where v_θ(S_t) is used as a baseline to reduce variance. It also uses multi-step return to further reduce the variance.

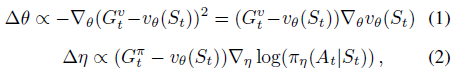
G^v_t and G^π_t are the estimated return of v_π(S_t) and Q_π(S_tA_t) respectively.

The agent follows the IMPALA distributed structure (several actors distributed across different environments, with a single GPU updating all rollouts with a deep convolutional ResNet followed by a LSTM recurrent layer), and implements importance sampling to correct each error term in n-step return. This causes the network to become unbiased but has high variance as a downside. To reduce variance, most of the importance sampling ratio is clipped. This lead to the v-trace return:

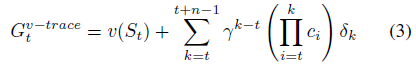
Following this, the returns used by the value and policy updates are:

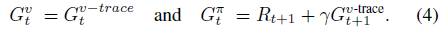
The network uses PopArt normalisation to derive a scale invariant algorithm for the actor-critic agent. In order to normalize both baseline and policy gradient updates, the value function v_µ,σ,θ(S) is parameterised as the linear transformation of a suitably normalised value prediction n_θ(S). The output from the deep neural net is the normalised value prediction:

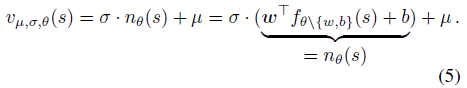
µ and σ are updated with (6) in order to track mean and standard deviation of the values.


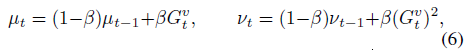
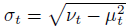
The fixed decay rate β determines the horizon used to compute the statistics. n_θ(S), µ and σ are used to normalise the loss in both value and policy network of the actor critic. This results in the scale-invariant updates:


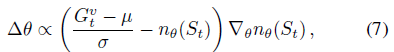
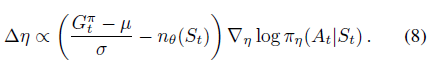
The normalised targets for values are non-stationary as they depend on statistics µ and σ. PopArt normalisation prevents this by updating the last layer of the normalised value network to preserve unnormalised value estimates v_µ,σ,θ, under any change in the statistics µ -> µ' and σ -> σ':

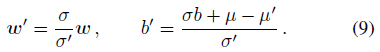
A single pair of normalisation statistics is not enough for multitask RL settings. Let D_i be an environment in some finite number i, and π(S|A) be a task-agnostic (it doesn't know which task it will get) policy that takes a state S from any of the environment D_i, and maps it to a probability distribution onto the shared action space A. The multi-task value function v(S) has N outputs, one for each task. v can be parameterised the same as before using Equation 5, except the statistics µ and σ are now vectors, and the same holds true for the value function, which becomes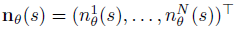

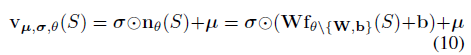
where W and b are the weights and bias for the last fully connected layer in n_θ(s). The scale invariant updates from Equation 7 and 8 now becomes:

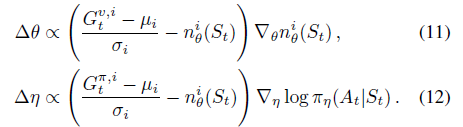
where the targets uses the value estimates for environment D_i for bootstrapping.

W and b are updated in the same way when updating µ and σ

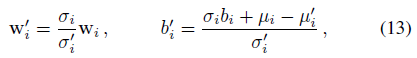
where w_i is the i^th row of matrix W, and µ_i, σ_i, b_i are the i^th elements of the corresponding parameter vectors. When updating, only the values, not the policy, are conditioned on the task index, so that the agent can perform without prior knowledge of the selected task. This is because values are only used to reduce the variance of the policy updates during training, not used for action selection.

To summarize, the gradients do not propagate into mean and std, as they are exclusively updated as in Equation 6. The weights W of the last layer of the value function are updated according to Equation 11 and 13. Note that the actor critic updates are applied first (11) before the update of the statistics (6), and finally followed by (13).

Result

The experiments are performed on Atari-57 and DmLab-30. In addition, an extra environment of Atari-57 without reward clipping is also introduced. Atari has a particularly diverse reward structure, while DmLab holds diverse tasks. The IMPALA baseline shown in this paper is also stronger than those reported in the original paper, as the agent has been equipped with a larger action set (e.g. giving it finer control when rotating).

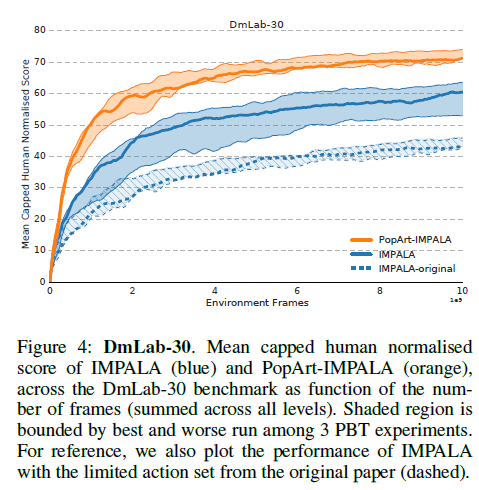
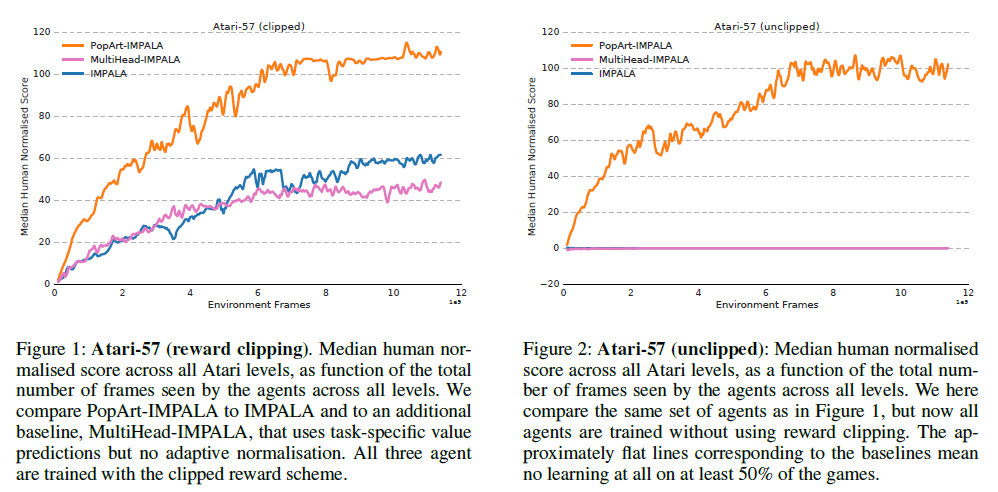
Note that the performance is the median performance of a single agent across all games, rather than the median of a set of individually trained agents.

The PopArt-IMPALA was further extended to incooperate pixel control in order to improve data efficiency.

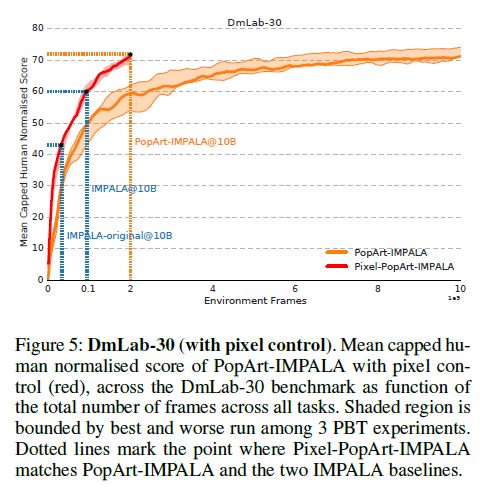
It can be seen in Figure 5 that pixel control augmented PopArt-IMPALA with only a fraction of the data. On top of this, since both PopArt and pixel control requires very small additional computational cost, the cost of training IMPALA agents is greatly reduced. Furthermore, any other orthogonal advances in deep RL can be combined to further improve performance, similar to those done by Rainbow.

Conclusion

The PopArt's adaptive normalisation has proven that it can allow a single agent to train across multiple tasks. On top of the performance gain, the data efficiency has also been improved. Further augmentations such as pixel control has shown to further boost data efficiency. Result might even be improved when incooperating other methods.