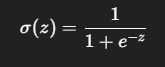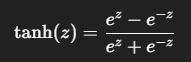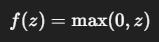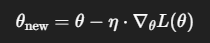Section1:入力層~中間層
ニューラルネットワークの基本構造:人間の脳の神経回路(ニューロン)を模倣した機械学習モデルで、以下の3つの主要な層から構成
| 層の名前 | 役割 |
|---|---|
| 入力層 | データを受け取る |
| 隠れ層 | 特徴を抽出・変換する(中間処理を行う) |
| 出力層 | 結果を出力する(分類・予測など) |
1.1 入力層(Input Layer)
外部からの入力データを受け取る層
画像認識ならピクセル、自然言語処理なら単語ベクトルなどが入力
28×28ピクセルの画像(白黒)の場合、784ノード(= 28×28)の入力層に
各ノードは単なる「値の受け渡し役」で、重みやバイアスは持たない
1.2 隠れ層・中間層(Hidden Layer)
入力データに対し、重み付き合計 + バイアスを計算し、活性化関数を適用して変換する。
より抽象的で意味のある特徴を抽出する中間処理層。
ネットワークの「学習能力」や「表現力」を左右。
(参考)中間層の深さと幅の関係
| 指標 | 内容 |
|---|---|
| 深さ | 層数を増やすとより複雑な関係を学習可能 |
| 幅 | 各層のノード数。増やすと精度向上する可能性があるが、過学習のリスクもある |
実装演習
多クラス分類(2-3-4のネットワークについて)
# 多クラス分類
# 2-3-4ネットワーク
# ウェイトとバイアスを設定
# ネートワークを作成
def init_network():
print("##### ネットワークの初期化 #####")
#試してみよう
#_各パラメータのshapeを表示
#_ネットワークの初期値ランダム生成
network = {}
input_layer_size = 3
hidden_layer_size=50
output_layer_size = 6
#試してみよう
#_各パラメータのshapeを表示
#_ネットワークの初期値ランダム生成
network['W1'] = np.random.rand(input_layer_size, hidden_layer_size)
network['W2'] = np.random.rand(hidden_layer_size,output_layer_size)
network['b1'] = np.random.rand(hidden_layer_size)
network['b2'] = np.random.rand(output_layer_size)
print_vec("重み1", network['W1'] )
print_vec("重み2", network['W2'] )
print_vec("バイアス1", network['b1'] )
print_vec("バイアス2", network['b2'] )
return network
# プロセスを作成
# x:入力値
def forward(network, x):
print("##### 順伝播開始 #####")
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 1層の総入力
u1 = np.dot(x, W1) + b1
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総入力
u2 = np.dot(z1, W2) + b2
# 出力値
y = functions.softmax(u2)
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("出力1", y)
print("出力合計: " + str(np.sum(y)))
return y, z1
## 事前データ
# 入力値
x = np.array([1., 2., 3.])
# 目標出力
d = np.array([0, 0, 0, 1, 0, 0])
# ネットワークの初期化
network = init_network()
# 出力
y, z1 = forward(network, x)
# 誤差
loss = functions.cross_entropy_error(d, y)
## 表示
print("\n##### 結果表示 #####")
print_vec("出力", y)
print_vec("訓練データ", d)
print_vec("交差エントロピー誤差", loss)
以下のような結果となった
*** 出力 ***
[2.81982766e-01 2.00262180e-02 2.21775630e-09 5.87194676e-06
1.84131842e-03 6.96143824e-01]
shape: (6,)
*** 訓練データ ***
[0 0 0 1 0 0]
shape: (6,)
*** 交差エントロピー誤差 ***
12.028437592893008
Section2:活性化関数
活性化関数とは、ノードに入力された重み付きの合計値(線形な値)を、非線形な出力に変換する関数
活性化関数がないと、ネットワーク全体がただの線形変換になり、どんなに層を重ねても複雑なパターンを学習できない。
非線形関数を使うことで、非線形な問題・画像認識、自然言語処理などを扱えるようになる。
| 特徴 | 説明 |
|---|---|
| 出力範囲 | (0, 1) |
| 用途 | 確率の出力(2値分類) |
| 長所 | 出力が滑らかで微分可能 |
| 短所 | 勾配消失問題(値が極端に大きい or 小さいと勾配が小さくなり学習が進みにくくなる) |
| 特徴 | 説明 |
|---|---|
| 出力範囲 | (-1, 1) |
| 長所 | シグモイドより中心が0に近く学習が安定しやすい |
| 短所 | 同様に勾配消失の問題がある |
| 特徴 | 説明 |
|---|---|
| 出力範囲 | [0, ∞) |
| 長所 | 計算が非常に速い・勾配消失が起きにくい |
| 短所 | 負の入力で出力が常に0 → 「死んだニューロン問題(Dead ReLU)」が発生することがある |
Leaky ReLU
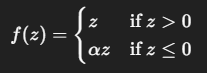
(※一般的に 𝛼 = 0.01など小さな定数)
ReLUの改良版。負の入力にも微小な勾配を与えることで、死んだニューロン問題を緩和
(参考)活性化関数の選び方
| 用途 | 推奨活性化関数 |
|---|---|
| 隠れ層 | ReLU(最も一般的)、Leaky ReLU |
| 出力層(2クラス分類) | Sigmoid |
| 出力層(多クラス分類) | Softmax |
| 時系列(RNNなど) | tanh または ReLU(+Gate構造) |
(参考補足)勾配消失と勾配爆発
勾配消失(vanishing gradient)
活性化関数の勾配が極端に小さくなると、誤差逆伝播時に重みがほとんど更新されず、学習が止まる。
勾配爆発(exploding gradient)
勾配が大きくなりすぎて重みが発散してしまい、ネットワークが不安定になる。
実装演習
# 中間層の活性化関数
# シグモイド関数(ロジスティック関数)
def sigmoid(x):
return 1/(1 + np.exp(-x))
# ReLU関数
def relu(x):
return np.maximum(0, x)
# ステップ関数(閾値0)
def step_function(x):
return np.where( x > 0, 1, 0)
Section3:出力層
出力層は、ニューラルネットワークが最終的な予測結果や判定結果を出力する層。
入力層 → 隠れ層 → 出力層 という流れの中で、最も最後に位置。
出力層の構成
1.前の層からの出力(隠れ層の出力)を受け取る
2.重み付き和を計算する
3.活性化関数を適用して、出力を整形(分類・回帰に応じた形式)
Softmax関数
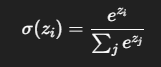
出力が確率分布(すべての出力が0〜1で合計1になる)
多クラス分類の出力層(例:数字の0〜9の分類など)
(参考)出力層のタスク設計について
| タスク種類 | ノード数 | 活性化関数 | 出力例 | 損失関数 |
|---|---|---|---|---|
| 2クラス分類 | 1 | Sigmoid | 0.87(87%の確率) | Binary Cross Entropy |
| 多クラス分類 | クラス数 | Softmax | [0.1, 0.7, 0.2] | Cross Entropy |
| 回帰 | 1(または多変量) | なし(恒等関数) | 25.3(例:温度) | MSE |
実装演習
# 出力層の活性化関数
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
Section4:勾配降下法
勾配降下法(Gradient Descent)は、ニューラルネットワークや機械学習モデルのパラメータ(重みやバイアス)を最適化するための基本アルゴリズム
⇒損失関数(Loss Function)を最小にするパラメータを見つける
パラメータ𝜃を次のように少しずつ更新
| 記号 | 意味 |
|---|---|
| $\theta$ | 現在のパラメータ(重みなど) |
| $\eta$ | 学習率(Learning Rate) |
| $\nabla_\theta L(\theta)$ | 損失関数の勾配(パラメータ方向の微分) |
学習率(Learning Rate) ⇒ 一回の更新の大きさ
小さすぎる:収束が遅い
大きすぎる:発散して収束しない
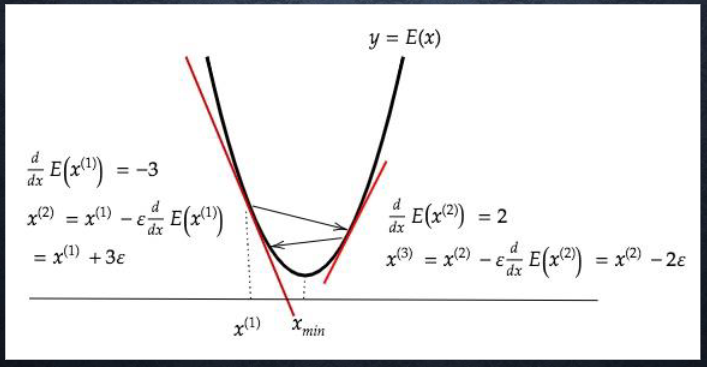
損失関数の谷底を目指すイメージ⇒勾配が小さくなる方向(=誤差が減る方向)に進む
勾配降下法の種類
-
バッチ勾配降下法(Batch Gradient Descent)
全データで損失を計算 → 一度に更新
精度高いが計算コストが重い(大規模データに不向き) -
確率的勾配降下法(Stochastic Gradient Descent, SGD)
1サンプルごとに勾配を計算して更新
ノイズが多いが計算が軽い → よく使われる -
ミニバッチ勾配降下法(Mini-Batch Gradient Descent)
少数のデータ(ミニバッチ)で更新
バッチとSGDのバランスが良く、実務で最も一般的
改良版アルゴリズム
| 名前 | 特徴 |
|---|---|
| Momentum | 過去の勾配方向を加味して滑らかに更新(慣性を持つ) |
| AdaGrad | パラメータごとに学習率を調整(よく更新されるパラメータは学習率を下げる) |
| RMSProp | 勾配の二乗平均で学習率を調整(AdaGradの改良) |
| Adam | Momentum + RMSProp を組み合わせた最強クラスの手法(実務で超定番) |
実装演習
# サンプルとする関数
#yの値を予想するAI
def f(x):
y = 3 * x[0] + 2 * x[1]
return y
# 初期設定
def init_network():
# print("##### ネットワークの初期化 #####")
network = {}
nodesNum = 10
network['W1'] = np.random.randn(2, nodesNum)
network['W2'] = np.random.randn(nodesNum)
network['b1'] = np.random.randn(nodesNum)
network['b2'] = np.random.randn()
# print_vec("重み1", network['W1'])
# print_vec("重み2", network['W2'])
# print_vec("バイアス1", network['b1'])
# print_vec("バイアス2", network['b2'])
return network
# 順伝播
def forward(network, x):
# print("##### 順伝播開始 #####")
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = functions.relu(u1)
## 試してみよう
#z1 = functions.sigmoid(u1)
u2 = np.dot(z1, W2) + b2
y = u2
# print_vec("総入力1", u1)
# print_vec("中間層出力1", z1)
# print_vec("総入力2", u2)
# print_vec("出力1", y)
# print("出力合計: " + str(np.sum(y)))
return z1, y
# 誤差逆伝播
def backward(x, d, z1, y):
# print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
#delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
## 試してみよう
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
delta1 = delta1[np.newaxis, :]
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
# print_vec("偏微分_重み1", grad["W1"])
# print_vec("偏微分_重み2", grad["W2"])
# print_vec("偏微分_バイアス1", grad["b1"])
# print_vec("偏微分_バイアス2", grad["b2"])
return grad
# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]
for i in range(data_sets_size):
data_sets[i] = {}
# ランダムな値を設定
data_sets[i]['x'] = np.random.rand(2)
## 試してみよう_入力値の設定
# data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
# 目標出力を設定
data_sets[i]['d'] = f(data_sets[i]['x'])
losses = []
# 学習率
learning_rate = 0.07
# 抽出数
epoch = 1000
# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)
# 勾配降下の繰り返し
for dataset in random_datasets:
x, d = dataset['x'], dataset['d']
z1, y = forward(network, x)
grad = backward(x, d, z1, y)
# パラメータに勾配適用
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
# 誤差
loss = functions.mean_squared_error(d, y)
losses.append(loss)
print("##### 結果表示 #####")
lists = range(epoch)
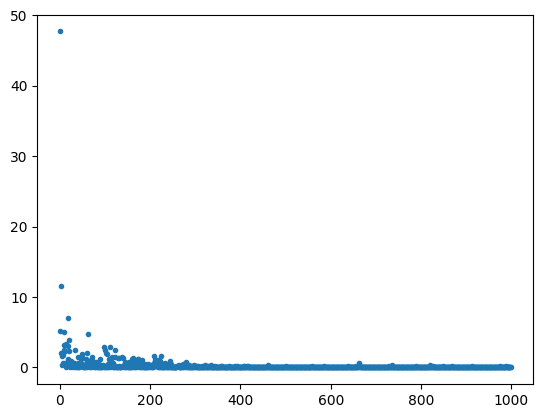
plt.plot(lists, losses, '.')
# グラフの表示
plt.show()
エポック数1000, 学習率0.07で確率的勾配降下法を行った結果
300以降で安定していることがわかる
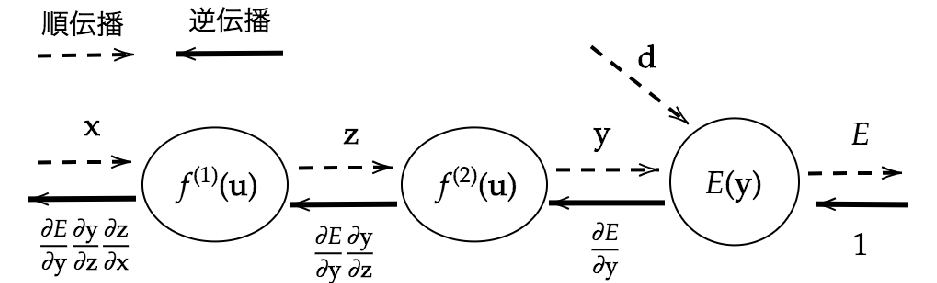
Section5:誤差逆伝播法(バックプロパゲーション)
誤差逆伝播法とは、出力層の誤差を出発点として、ネットワークの各層に“誤差”を逆向きに伝えていき、重みを更新するための勾配(偏微分)を求める手法
勾配降下法を行うには、損失関数の各パラメータに対する偏微分(勾配)が必要
しかし、層が深いネットワークではこの偏微分を手計算するのは困難
それを効率的に求めるのが、誤差逆伝播法。
誤差逆伝播法のイメージ
1.順伝播(forward propagation)
入力 → 出力まで、ネットワークを通して予測を行う
2.損失関数で誤差を計算(loss)
3.逆伝播(backpropagation)
損失関数の勾配を出力層から逆向きに計算
4.勾配降下法などでパラメータ(重み・バイアス)を更新
数式での表現
勾配の連鎖(連鎖率)
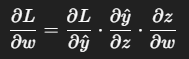
このようにして、出力層から順に各層の勾配を求めていくのが逆伝播の本質
実装演習
シンプルな1層ネットワークの誤差逆伝播法
import numpy as np
# シグモイド関数とその微分
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_deriv(x):
return sigmoid(x) * (1 - sigmoid(x))
# 入力と正解
x = np.array([[0.5]])
y_true = np.array([[1]])
# 重みとバイアス
w = np.array([[0.8]])
b = np.array([[0.1]])
# 順伝播
z = np.dot(x, w) + b
a = sigmoid(z)
loss = 0.5 * (y_true - a)**2
# 逆伝播(勾配)
dL_da = -(y_true - a)
da_dz = sigmoid_deriv(z)
dz_dw = x
# 勾配の連鎖
dL_dw = dL_da * da_dz * dz_dw
# パラメータ更新(学習率 η=0.1)
w -= 0.1 * dL_dw