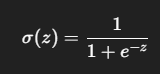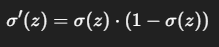Section1:勾配消失問題
誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。
そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。
| 原因 | 説明 |
|---|---|
| 活性化関数の特性 | Sigmoid/tanhは微分値が0〜1未満 → 勾配が減衰しやすい |
| 深いネットワーク構造 | 層が多いほど連鎖律での微分積が小さくなりやすい |
| 重みの初期値 | 不適切な初期化だと勾配が早い段階で消える |
| 過小な学習率 | 微小な勾配 × 小さい学習率 → ほぼ更新されない |
活性化関数の影響比較
| 関数 | 微分の最大値 | 勾配消失しやすさ | 備考 |
|---|---|---|---|
| Sigmoid | ~0.25 | 高い | 出力も飽和しやすい |
| tanh | ~1.0 | 中程度 | 中心が0だが依然小さい |
| ReLU | 0 or 1 | 低い | x > 0なら勾配がそのまま通る |
| Leaky ReLU | 常に非ゼロ | 非常に低い | 勾配消失ほぼなし |
この表より、シグモイド関数は勾配消失を起こしやすいため、その代わりにReLU関数が用いられる
また、そのほかにも以下に勾配消失の解決策・手法をまとめる
解決策(代表的な手法)
| 解決策 | 説明 |
|---|---|
| ReLU活性化関数 | 微分値が1(x > 0のとき) → 勾配が消えにくい |
| 重み初期化の工夫 | Xavier初期化, He初期化など。出力の分散を維持する |
| Batch Normalization | 中間層の出力を正規化し、勾配が安定する |
| 残差接続(Residual Connection) | ResNetのような構造で“勾配の通り道”を作る |
| 勾配クリッピング | 勾配が大きすぎる/小さすぎる時に制限をかける(主にRNN) |
確認テスト
よって, 答えは(2) 0.25
実装演習
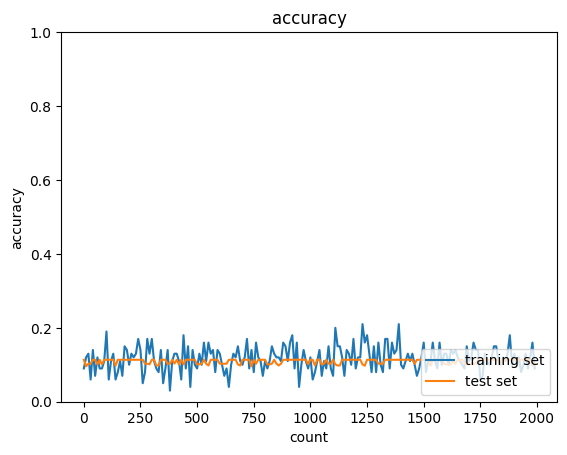
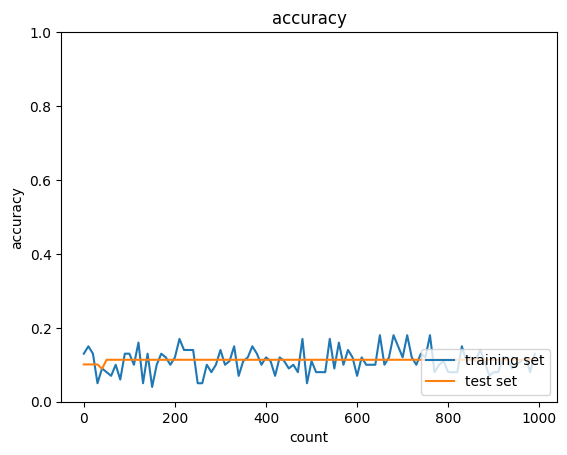
シグモイド関数による勾配消失
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01)
iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
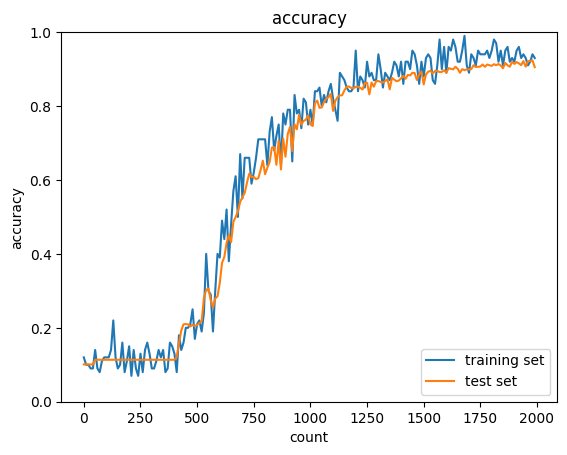
ReLU関数にて同じ条件で試す
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std=0.01)
iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
確かに、ReLU関数を用いると、シグモイド関数よりAccuracyが高く改善された。
Section2:学習率最適化手法
学習率とは、パラメータ更新のステップサイズであり、次の式における𝜂に該当
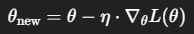
| 値が小さい場合 | 値が大きい場合 |
|---|---|
| 学習が非常に遅くなる | 発散して不安定になる可能性がある |
この問題を解決するために以下のような改善案があげられる
適応的学習率アルゴリズム(Adaptive Learning Rate)・(確認テスト)
勾配の履歴や大きさに応じて、パラメータごとに学習率を調整する手法
| 手法 | 特徴 | 主な用途 |
|---|---|---|
| モメンタム | 勾配が同じ方向に続く場合、「加速」してより早く最小値にたどりつくようにする。 | SGDの拡張 |
| AdaGrad | よく変化するパラメータは学習率を下げる | スパースデータ(例:NLP) |
| RMSProp | AdaGradの学習率低下を緩和 | RNNやオンライン学習 |
| Adam | Momentum + RMSProp の組み合わせ | 最も広く使われる |
| Adadelta / Nadam / AdamW | それぞれの改良版 | タスクに応じて選定 |
実装演習
通常のSGDによる実装
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 ================================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Momentumを使用したときの実装
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 ================================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
# 慣性
momentum = 0.9
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
v = {}
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
v[key] = np.zeros_like(network.params[key])
v[key] = momentum * v[key] - learning_rate * grad[key]
network.params[key] += v[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Adamを用いた実装
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 ================================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
beta1 = 0.9
beta2 = 0.999
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
m = {}
v = {}
learning_rate_t = learning_rate * np.sqrt(1.0 - beta2 ** (i + 1)) / (1.0 - beta1 ** (i + 1))
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
m[key] = np.zeros_like(network.params[key])
v[key] = np.zeros_like(network.params[key])
m[key] += (1 - beta1) * (grad[key] - m[key])
v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])
network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
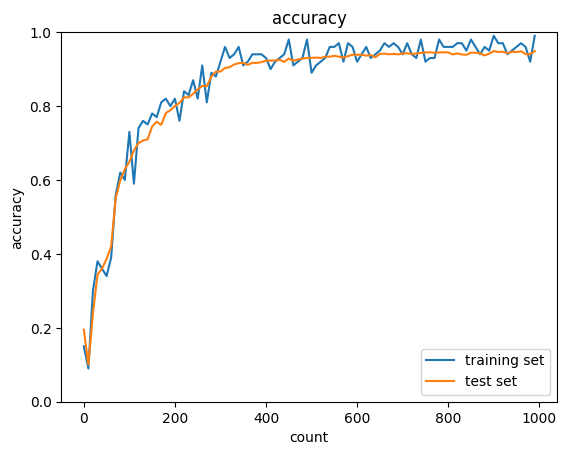
図を見て明らかなようにAdamを用いたものはMomentumと比べてAccuracyが向上した
Section3:過学習
テスト誤差と訓練誤差とで学習曲線が乖離する

そのため、特定の訓練サンプルに対して特化して学習する
| 原因 | 説明 |
|---|---|
| モデルが複雑すぎる | パラメータが多すぎて、ノイズまで表現できてしまう |
| 学習データが少ない | 全体のパターンを代表していないため、例外に過剰適応する |
| エポック数が多すぎる | 訓練誤差を減らしすぎて、汎化性能が下がる |
| ラベルに誤りがある | ノイズに対応しようとしてしまう |
主な対策
| 対策 | 説明 |
|---|---|
| データを増やす | より多様なデータを学習することで、過剰適合を防ぐ |
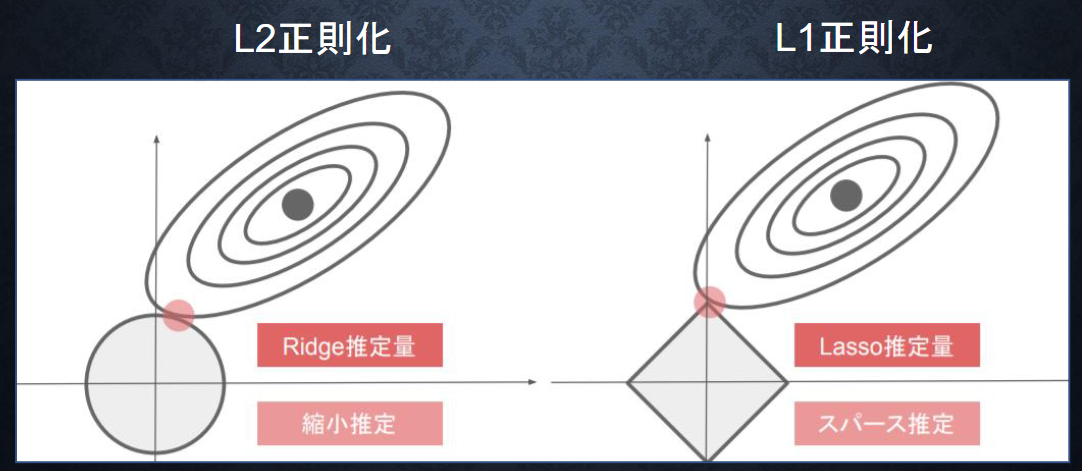
| 正則化(Regularization) | 不必要なパラメータの影響を弱める(L1/L2正則化) |
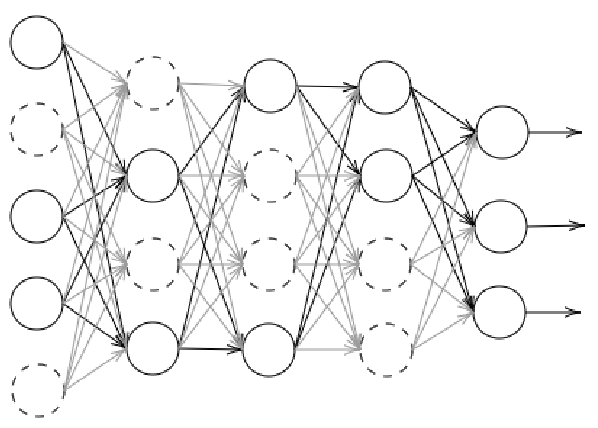
| ドロップアウト(Dropout) | 学習中にランダムで一部のノードを無効化し、依存を防ぐ |
| 早期終了(Early Stopping) | 検証誤差が悪化し始めたら学習を止める |
| データ拡張(Augmentation) | 特に画像などで有効。回転・反転などしてデータを“水増し”する |
| モデルの簡素化 | 層やノード数を減らして表現力を制限する |
| クロスバリデーション | 安定した汎化性能を確認しながら学習する |
確認テスト

リッジ回帰は、重みの大きさを抑えることで過学習を防ぐための手法。
L2正則化とも呼ばれ、損失関数に「重みの2乗和」をペナルティ項として加える。
ハイパーパラメータ(通常は𝜆や𝛼)はその強さを制御。
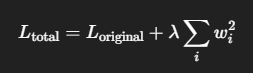
A.(1)
リッジ回帰のペナルティは「重みの大きさ」を抑える。
ハイパーパラメータが大きくなるほど強制力が増し、重みが0に近づく(ただし完全な0にはならない)。
実装演習
学習データの不足により、過学習を引き起こす
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = optimizer.SGD(learning_rate=0.01)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
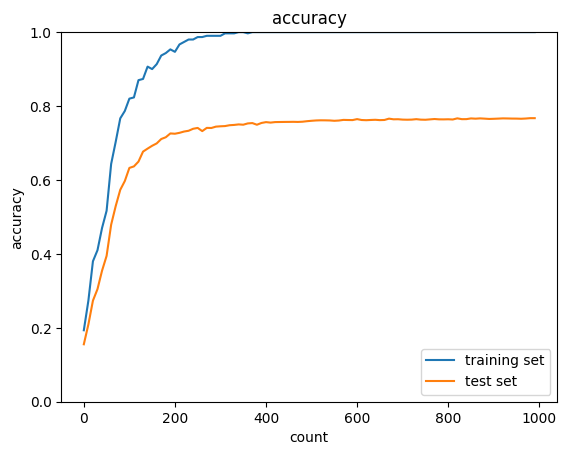
過学習により訓練データとテストデータの結果に乖離が発生している
L2正則化を実装
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.1
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
過学習時の結果よりもテストデータのAccuracyが明らかに向上している
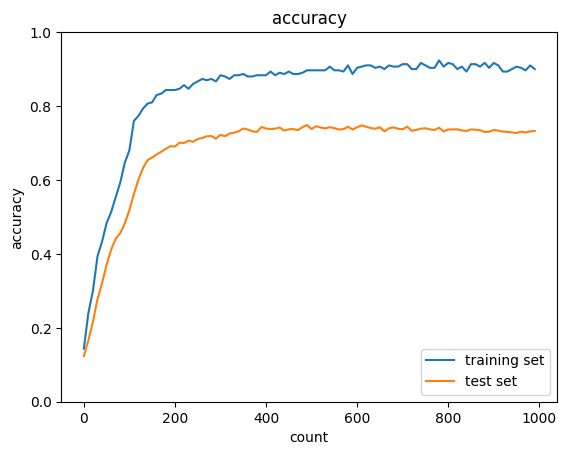
L1正則化を実装
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.005
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Section4:畳み込みニューラルネットワークの概念
畳み込みニューラルネットワーク(CNN)は、画像や音声などの多次元データの特徴を抽出・分類するための深層学習モデル。入力データの局所的な構造を捉えるのが得意
主に画像認識、物体検出、顔認識、医療画像診断などに使われる
CNNの構造イメージ
畳み込み層(Convolutional Layer)
画像の小領域ごとにフィルタ(カーネル)をかけて特徴を抽出する。
フィルタは学習によって最適化される。
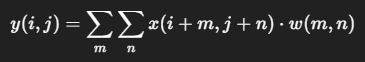
| 項目 | 内容 |
|---|---|
| $x$ | 入力画像の画素 |
| $w$ | カーネル(フィルタ) |
| $y$ | 出力特徴マップ(Feature Map) |
プーリング層(Pooling Layer)
特徴量の次元削減(ダウンサンプリング)
位置の変化に強い(平行移動など)頑健性を持たせる
| 名前 | 内容 |
|---|---|
| Max Pooling | 局所領域の最大値を取得(最も一般的) |
| Average Pooling | 平均値を取る |
全結合層(Fully Connected Layer)
畳み込み層とプーリング層で抽出した特徴を元に分類や回帰を行う層
通常、最後の数層で使用
出力層(Output Layer)
Softmax関数などで各クラスの確率を出力
例:手書き数字認識(0〜9の10クラス)
(参考)CNNとニューラルネットワークの違いについて
| 項目 | CNN | 通常のNN |
|---|---|---|
| 対象 | 画像や時系列など空間構造があるデータ | 数値・ベクトルなど一般的データ |
| 特徴抽出 | 自動(カーネルで) | 明示的に特徴量を入力する必要あり |
| パラメータ数 | 少ない(カーネル共有) | 多くなりがち |
| 空間構造の保持 | 可能 | 不可能 |
(補足)CNNが効果的な理由
| 特徴 | 説明 |
|---|---|
| 局所受容野 | 小さな領域ごとに特徴を抽出(全体を一度に見ない) |
| パラメータ共有 | 同じフィルタを画像全体に適用 → 計算効率・精度向上 |
| 階層的特徴抽出 | 低レベル(エッジ)から高レベル(形・物体)まで段階的に学習 |
実装演習
畳み込み層
class Convolution:
# W: フィルター, b: バイアス
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中間データ(backward時に使用)
self.x = None
self.col = None
self.col_W = None
# フィルター・バイアスパラメータの勾配
self.dW = None
self.db = None
def forward(self, x):
# FN: filter_number, C: channel, FH: filter_height, FW: filter_width
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
# 出力値のheight, width
out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
# xを行列に変換
col = im2col(x, FH, FW, self.stride, self.pad)
# フィルターをxに合わせた行列に変換
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
# 計算のために変えた形式を戻す
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
# dcolを画像データに変換
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
プーリング層
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# xを行列に変換
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
# プーリングのサイズに合わせてリサイズ
col = col.reshape(-1, self.pool_h*self.pool_w)
# 行ごとに最大値を求める
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
# 整形
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
simple convolution network class
class SimpleConvNet:
# conv - relu - pool - affine - relu - affine - softmax
def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# レイヤの生成
self.layers = OrderedDict()
self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = layers.Relu()
self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = layers.Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = layers.Relu()
self.layers['Affine2'] = layers.Affine(self.params['W3'], self.params['b3'])
self.last_layer = layers.SoftmaxWithLoss()
def predict(self, x):
for key in self.layers.keys():
x = self.layers[key].forward(x)
return x
def loss(self, x, d):
y = self.predict(x)
return self.last_layer.forward(y, d)
def accuracy(self, x, d, batch_size=100):
if d.ndim != 1 : d = np.argmax(d, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
td = d[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == td)
return acc / x.shape[0]
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grad = {}
grad['W1'], grad['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grad['W2'], grad['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grad['W3'], grad['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grad
from common import optimizer
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)
print("データ読み込み完了")
# 処理に時間のかかる場合はデータを削減
x_train, d_train = x_train[:1000], d_train[:1000]
x_test, d_test = x_test[:200], d_test[:200]
network = SimpleConvNet(input_dim=(1,28,28), conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
処理に時間がかかるため訓練データを1000, テストデータを200にしたが、それでも10分ほど処理に時間がかかった
訓練データとテストデータに若干乖離が見られたもののAccuracyは安定して高く見られた

Section5:最新のCNN
AlexNet(アレックスネット)は、2012年のImageNet Large Scale Visual Recognition Challenge(ILSVRC)で圧倒的な性能を発揮し、ディープラーニングブームのきっかけを作ったCNNモデル
(参考)AlexNetは5つの畳み込み層+3つの全結合層のCNN
入力画像(224×224×3)
↓
Conv1(96 filters, 11×11, stride 4)→ ReLU → LRN → MaxPool
↓
Conv2(256 filters, 5×5)→ ReLU → LRN → MaxPool
↓
Conv3(384 filters, 3×3)→ ReLU
↓
Conv4(384 filters, 3×3)→ ReLU
↓
Conv5(256 filters, 3×3)→ ReLU → MaxPool
↓
Flatten
↓
FC1(4096)→ ReLU → Dropout
↓
FC2(4096)→ ReLU → Dropout
↓
FC3(1000)→ Softmax
LRN(Local Response Normalization)※現在ではあまり使われない
隣接ノード間での正規化。
一時的に精度改善に寄与するとされた。
Dropout
過学習を防ぐためにFC層で50%のノードをランダム無効化。
過学習への対策として初めて大規模に導入された。
Section6:[フレームワーク演習] 正則化/最適化
| 概念 | 正則化 | 最適化 |
|---|---|---|
| 目的 | 過学習の防止 | 損失関数の最小化(学習) |
| 手法の対象 | モデル構造や損失関数 | パラメータの更新方法 |
| 関係 | 正則化項が損失関数に加えられ、それを最適化アルゴリズムで最小化する |
L2正則化(リッジ回帰)

大きな重みを抑制
学習は続くが、滑らかなモデルになる
ニューラルネットやロジスティック回帰でよく使う
L1正則化(ラッソ回帰)
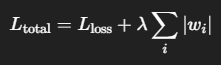
不要な重みを0に近づける(=特徴選択)
自然にスパースな(ゼロの多い)モデルを作れる
Dropout
過学習を防ぐためにFC層で50%のノードをランダム無効化。
過学習への対策として初めて大規模に導入された。
Batch正規化
各層への入力を正規化(平均0、分散1に)することで、学習を安定化させる手法
勾配消失や勾配爆発の緩和,学習率の設定が楽になる
正則化効果(Dropoutなしでも過学習が減る)

H x W x CのsampleがN個あった場合に、N個の同一チャネルが正規化の単位 。
ミニバッチのサイズを大きく取れない場合には、効果が薄くなってしまう
実装演習
データのロード
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
x_train = x_train / 255
x_test = x_test / 255
y_train = tf.one_hot(y_train.reshape(len(y_train)), depth=10)
y_test = tf.one_hot(y_test.reshape(len(y_test)), depth=10)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
index2label = {
0: 'airplane',
1: 'automobile',
2: 'bird',
3: 'cat',
4: 'deer',
5: 'dog',
6: 'frog',
7: 'horse',
8: 'ship',
9: 'truck'
}
import matplotlib.pyplot as plt
import random
index = 0
count = 50
plt.figure(figsize=(16, 10))
for i, img in enumerate(x_test[index:index+count]):
plt.subplot(5, 10, i + 1)
plt.imshow(img)
plt.axis('off')
plt.title(index2label[np.argmax(y_test[i])])
plt.show()
ベースモデルでの実行(正則化なし)
epochs = 5
batch_size = 256
def create_model(input_shape, class_num):
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, 3, padding='same', input_shape=input_shape[1:], activation='relu'),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(class_num, activation='softmax'),
])
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['acc'])
return model
model = create_model(x_train.shape, 10)
model.summary()
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
batch_size=batch_size, epochs=epochs)
Epoch数が増えるごとにAccの上昇と損失関数の低減を確認した
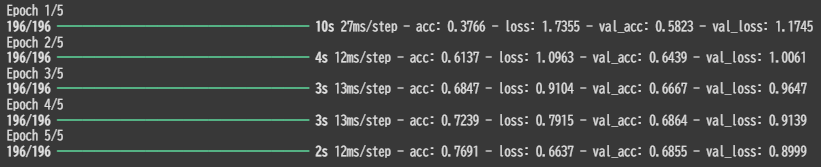
L2正則化の実効例(出力直前の全結合層においてL2正則化を適用)
def create_model(input_shape, class_num):
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, 3, padding='same', input_shape=input_shape[1:], activation='relu'),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu', activity_regularizer=tf.keras.regularizers.L2(0.01)),
tf.keras.layers.Dense(class_num, activation='softmax'),
])
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['acc'])
return model
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
batch_size=batch_size, epochs=epochs)
正則化してない場合と比べて数値的にはほとんど同じような結果となった
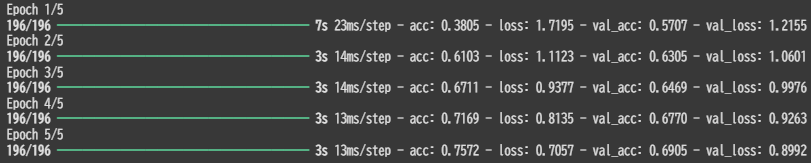
L1正則化の実効例
def create_model(input_shape, class_num):
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, 3, padding='same', input_shape=input_shape[1:], activation='relu'),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu', activity_regularizer=tf.keras.regularizers.L1(0.01)),
tf.keras.layers.Dense(class_num, activation='softmax'),
])
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['acc'])
return model
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
batch_size=batch_size, epochs=epochs)