0.はじめに
大学で統計学の講義を受講している者です。
用語や概念をまとめて以下の項目に分類しています。
統計学学習全体像
【統計学】概要
【統計学】度数・偏差・分散
【統計学】係数・回帰
【統計学】集計表
【統計学】集団・標本
【統計学】分布
【統計学】期待値・推定・信頼度
【統計学】統計的検定
1.傾向
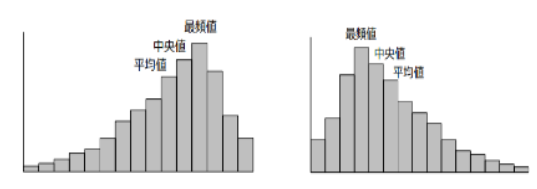
分布の傾向
下がっている側に平均値が見られる傾向がある
左側に下がっているグラフ
平均値⇒中央値⇒最頻値の順になるのが一般的
右側に下がっているグラフ
最頻値⇒中央値⇒平均値の順になるのが一般的
(日本国民の給料値、最頻額は平均の給与より低い)
散布図の傾向
散布図内のプロットが密集している場合は関係が強い傾向がある
右上がり、右下がりで関連の強さが把握できる
正/負の相関によって分布に特徴が表れる
2.二項分布(B)
関数(s:成功数\,\,,\,\,n;試行回数\,\,,\,\,p:Sの生起確率)
= BINOM.DIST(s,n,p,FALSE)
n回数ベルヌーイ試行を行った結果の成功(S)した回数xの確率分布のこと
例としてコインを3回投げた時の表の出る回数x
試行回数を大きくすると正規分布に近づく
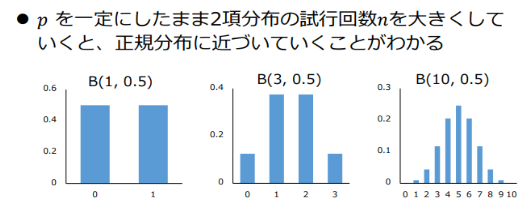
表現方法
B(n,p)として表す
試行回数10の成功(S)の生起確率が0.5の場合:B(10,0.5)
不良品率pの多数の製品の中からn個の製品を無作為に取り出した時、
その中に含まれる不良品の個数xの二項分布はB(n,p)
確率関数
p(x)として表す
n:試行回数\,\,,\,\,x:成功回数\,\,,\,\,S:成功の事\,\,,\,\,F:失敗回数
p(x) = nCx × px × (1-p)n-x
nCx と px と(1-p)n-xに分けて考える
-
nCx・・・①
組み合わせのこと
6個のうち3個取り出す組み合わせは6C3
したがってn回の試行のうち成功Sがx回起こる場合はnCx -
px・・・②
確率pの成功Sがx回起こる確率はp × x
よってpx -
(1-p)n-x・・・③
失敗の数を求めたい
全体1から確率pを引き成功Sの回数nから
成功回数のxを引いた数を掛ければ失敗確率が求められる
よって(1-p)n-xとなる
失敗回数を掛けるのには失敗回数含めての確率を求めるのが二項分布のため
②の成功と③の失敗の確率で起こる
nCx通りあるので掛け合わせることで二項分布の確率関数を得ることができる
二項分布を利用した指標
期待値・分散が求められる
全体回数:n、確率:pをした場合、
- 二項分布→期待値の求め方
期待値E(x) = np
- 二項分布→分散の求め方
分散V(x) = np(1-p)
例題
とある企業にて
全体の60%の社員が食堂を利用したことがない
無作為に選んだ5人の社員のうち、4人以上が利用したことがないという確率はいくつか
A.
二項分布で求める
利用したことがない確率は0.6
試行回数nは5人のため5回
成功数s:4人以上のため4、と5人のときも考えなければいけないので5も計算をする
BINOM.DIST(4,5,0,6,FAISE) = 0.25
BINOM.DIST(5,5,0.6,FALSE) = 0.07
0.25 + 0.07 =0.32
約32%が利用したことがないことになる
3.ポアソン分布
関数
= POISSON.DIST(生起回数,λ,FALSE)
稀な現象が起こる生起回数の確率
ある期間に平均λ回起こる現象がある期間のx回起こる確率の分布がポアソン分布
二項分布と近しい分布の一つ
ポアソン分布 ≒ 二項分布
n×p
二項分布においてはnpは期待値としていたが
ポアソン分布においてはλ = npとして表す
これはnを限りなく大きくしてpを限りなく小さくするといった
極限についての式となる
λ
平均値と考えていい
npは期待値、よってλ = np(期待値)
期待値は平均値
λが大きくなるほどグラフが左右対称になっていく
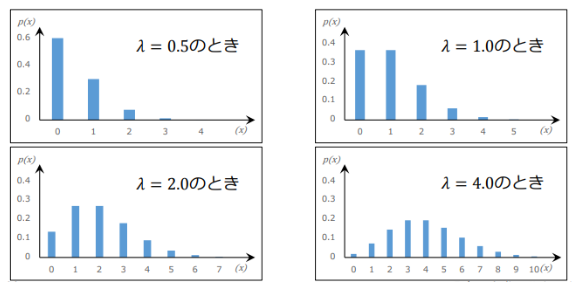
4.正規分布(N)
関数
NORM.DIST(xの値,平均,標準偏差,TRUE)
平均値と最頻値と中央値が一致し左右対称となっている分布
釣鐘型、左右対称のパターンの際の確率モデルとして正規分布がよく用いられる
標本数が十分大きい場合には正規分布が使用される
(標本数が小さい場合にt分布が使用)
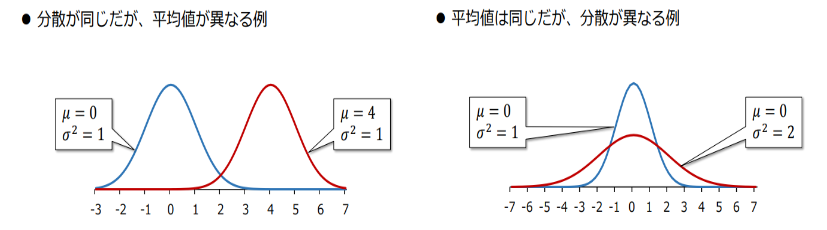
平均値と分散の値によって形状が決まる
標準正規分布
平均が0、分散が1の正規分布
表現方法N(μ,σ²)
(平均,分散)として表す
平均50、分散10の正規分布である場合はN(50,10)
例題
学生の平均身長は168cm
分散は49
標準偏差は分散の平方根のため7
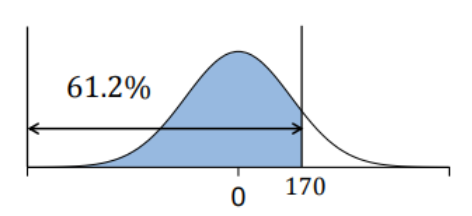
身長が170cm以下の割合を求めよ
A.
=1-(NORM.DIST(168,170,7,true))
結果0.612となり61.2%の割合がいる
5.t分布
関数
t_df=T.INV.2T(両側確率,自由度)
自由度に応じたさまざまな分布の総称のこと
標本数が小さい場合にt分布が使用される
(標本数が十分大きい場合には正規分布)
母標準偏差σを標本不偏標準偏差Sで代用した値をtと置く
二項分布→正規分布と同様に自由度が大きくなるほど標準正規分布に近づいていく
記号
| 記号 | 詳細 |
|---|---|
| tdf | 自由度 |
| s | 標本標準偏差 |
| n | 標本サイズ |
| x̄ | 標本平均 |
| μ | 母集団平均 |
Xがt分布に従うとき以下の計算式を用いる
t分布 = \frac{標本平均-母集団平均}{標本標準偏差×\sqrt{標本サイズ}・・・①}
t = \frac{\bar{x}-μ}{s\sqrt{n}}
ある値x⁻が与えられたときt分布の中で
どれくらいの標準偏差に位置するかを表す式が以下となる
t分布の位置 = 標本平均-自由度×① , 標本平均+自由度×①
\bar{x}-t_df × s\sqrt{n}\,\,\,\,,\,\,\bar{x}+t_df × s\sqrt{n}
例題
日本人の20~24歳男性の平均身長を知りたいので標本として16人を無作為抽出し身長を測定した結果
平均171.95、標準偏差5.59cmであった。また母集団は正規分布にしたがっているが
母分散は未知であるものとする。母平均の95%信頼区間を求める
<n =16 、標本平均x̄ = 171.95、標準偏差S = 5.59>
A.
1.標本が小さいため自由度16から-1を行う
t分布計算方法
T.INV.2Tを自由度15と両辺確率0.05で行う
tdf =T.INV.2T(0.05,15) = tdf は2.13となる
これにより自由度15の95%(上下5%区間)tdf = 2.13
しかしここで求めた区間(tdf)は母平均μの95%信頼区間ではない
自由度dfのt分布95%の面積に対するt値の範囲となる
t分布を用いた信頼区間式に値を代入し計算する
2.自由度15の95%(上下5%区間)tdfを使い信頼区間を求める
(x̄ - tdf * s/√n)、(x̄ + tdf * s/√n)
171.95 - 2.13 × 5.59√16、171.95 + 2.13 × 5.59/√16
解は(168.97,174,93) となる
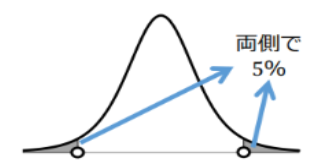
両側検定
"p値を用いる場合"と"臨界値を用いる場合"の2つの方法がある
p値を用いる場合
関数
p値 = T.DIST.2T
6.カイ二乗分布
関数
=CHISQ.INV.RT(上側確率,自由度)
=CHISQ.INV.(下側確率,自由度)
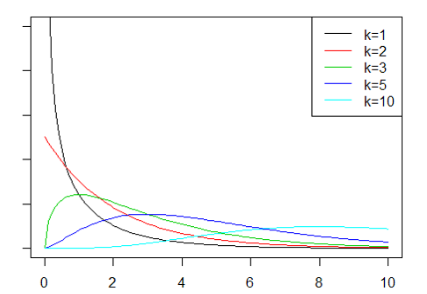
自由度によって形が変わる分布
自由度が大きくなるほど頂上が右側に寄っていく
上位側と下位側の計算の二通りが必要
上側を求める場合RTを記述する。下側を求める場合は関数名RTなしの記述となる