0.はじめに
大学で統計学の講義を受講している者です。
用語や概念をまとめて以下の項目に分類しています。
統計学学習全体像
【統計学】概要
【統計学】度数・偏差・分散
【統計学】係数・回帰
【統計学】集計表
【統計学】集団・標本
【統計学】分布
【統計学】期待値・推定・信頼度
【統計学】統計的検定
1.期待値(E(x),μ)
確率的に得られる値の平均値
起こりうる事象で得られる値とそれが起こる確率の積を足し合わせる
計算式
{x個数 × 確率p(x) }の総和
\sum_{k=1}^{n} x_kP_k
平均値との関係
-
平均値:回数試行した場合の値の合計を試行回数で割ったもの -
期待値E(x):値(xi)×確率(pi)を全て足して得られる結果の期待される値
E(x) = \sum_{i = 1}^n{}x_ip_i
母平均μ = 標本平均の期待値E(x)
大数の法則により母平均と標本平均の期待値は等しい
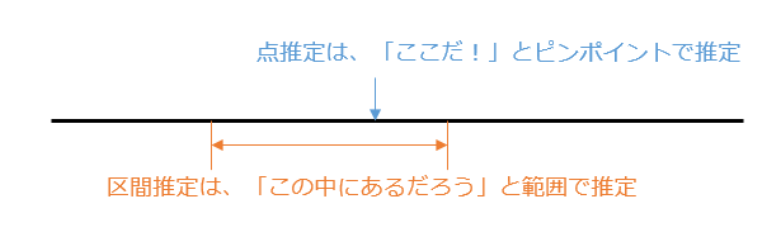
2.点推定・区間推定
点推定
標本より600世帯に調査を行ったところ240世帯が視聴している番組がある
この場合の母集団の視聴率は240/600 ×100 = 40%
おおよそ母集団は40%と判断できる
区間
母数がここから~ここら辺にあるのではないかという範囲
区間の幅は信頼度という指標により誤差範囲が異なる
区間推定
標本より600世帯に調査を行ったところ240世帯が視聴している番組がある
この場合の母集団の視聴率は240/600 ×100 = 40%
±4誤差として考えると、36~44%程に収まる範囲となる
3.信頼度
母数を含んでいるか信頼できる度合い
信頼度95%について
95%に母数が含まれているような区間の作りのこと
母数が入っている確率が95%というわけではない
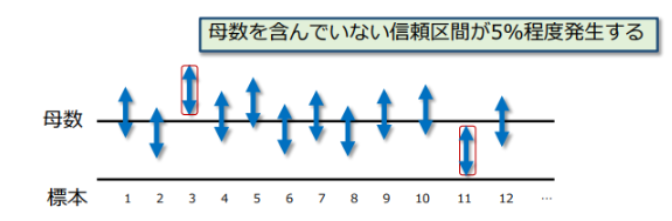
100回のうち95回は真、5回は偽である範囲
→全体のうち95%程度の回数で信頼区間の中に母数が含まれているような区間の作り
信頼区間
範囲のこと
先述でもしたが100回中5回は外れるが95回は母数が含まれるような区間のこと
関数
=NORM.INV(上側/下側の確率,平均,標準偏差)
例題
日本人の20~24歳男性の平均身長を知りたいので標本として1516人を無作為抽出し
身長を測定した結果、平均171,95cmだった。また母集団は正規分布に従い
標準偏差は経験的に5.59cmであるとする。
母平均の点推定値及び95%信頼区間を求める
<全体n = 1516、標本平均期待値 = 171.95、標準偏差 = 5.59>
A.
1.母平均μは標本平均の期待値である
よって171.95が平均となる
2.95%信頼区間を関数NORVで求める
上側と下側と確率を分けて考える
上側確率は100-95 = 2.5%下側確率は100-2.5 = 97.5%
3.標本平均の標準偏差を求める
問題文より母集団の標準偏差(σ)は5.59
V(x̄)の標準偏差はσ / √nで求めらえる
5.59/ √1516 = 0,144
この値を関数に使用する
4.計算
=NORMINV(0.025,171.95,0.144) = 171.67
=NORMINV(0.975,171.95,0.144) = 172.23
よって母平均の95%信頼区間171.67~172.23cmとなる