この記事はJDLA E資格認定講座のラビットチャレンジの成果レポートである。
特に、理解しづらい概念、意味づけなどで腑に落ちるまで調べる中で得た知見を中心に記載しているのこれからE資格の学習を始める方にご参考になると幸いである。
1.E資格における応用数学の概要
●E資格の「応用数学」は大学レベルの数学(※)全般を対象としているのではなく、機械学習(Machine Learning,以下「ML」)や深層学習(DeepLearning、以下「DP」)に関連が深い分野の知識を問うことを主眼としている。
①線形代数 特に行列、特異値分解、特異値分解、ノルム
②確率・統計 ベルヌーイ分布、マルチヌーイ分布、ガウス分布、ベイズ則
③情報理論 エントロピー、交差エントロピー、KLダイバージェンス
(※)大学レベルの数学の分野は、線形代数、微分積分、統計学、複素数関数、ベクトル解析、常微分方程式、偏微分方程式、フーリエ解析、ラプラス変換など広範囲に渡る。
●その意味では数学全体の中では非常に限られた分野の出題と言えるが、それでも関係学部(院)で学習をしていなければ、いきなり大学レベルの数学を学習すると理解不能となるため、高校数学の微分積分、行列等の復習が必要となる。そうかといって最初から高校数学から始めると膨大な時間がかかるので、E資格のテキスト、問題にあたりながら理解が難しいところを高校レベルまで戻るというやり方が効果的である。
(参考:高校レベル(+α)の数学を分かりやすく解説しているサイト)
高校数学の美しい物語 https://manabitimes.jp/math
●講義やテキストに基づき学習を進めると、例えば線形代数では行列の積、逆行列、行列式の求め方などを順次習得できる。一方、これらの算術とML、DLがどのように使われるのかが分からないと具体的な計算の手順だけを覚えて問題は解けるけど何をしているのかという本質的な理解につながらない。この点は鶏と卵の関係であり、応用数学、ML、DLを何周かする中で相互の関係が理解できる。
以下の記載の中では、ML,DLも学習しつつ応用数学に戻ってきて理解したことや気づいたことなどを中心に記載する。
線形代数の深い理解は、多くの機械学習アルゴリズム、特に深層学習の理解と取り扱いに不可欠である。
ー「深層学習」(Goodfellow et al,2016)
2.線形代数
(1)ML、DLにおける線形代数
●多くの要素を捨象してML,DLの本質を一言でいえば、
”何か数字をマジックボックスに入れると、ポンとある数字(答えであったり確率であったりする)が出る”
ということである。
●このマジックボックス部分は、数学でいう関数(要はy=ax+bのような式)であり、その論理や操作技術の知恵が線形代数である。線形代数の道具を使うことで変数・数値をまとめて簡単に扱えるようになる。
●例を挙げる。マジックボックスの中身は関数はいちいち手で計算すれば答えは出るが面倒である。計算はコンピュータにさせればいいのだがどのように動くかは予め指図をしなければ動いてくれない。そこでどのように動くかの指針を出すのに数学の道具を借りてくるのである。ブラックボックスの中身は関数の式だが、答え(凸関数曲線の谷底になっている部分)まで自動的に達するように、どちらの方角に進めばいいかを滑らかな曲線に対する傾き(微分)を利用する。
機械学習の理論では線形代数で用いられる概念が多く登場します。 これらの概念を利用することで、複数の値や変数をまとめて扱うことができるようになり、数式を簡潔に表現できるようになります。
https://tutorials.chainer.org/ja/05_Basics_of_Linear_Algebra.html
●また、ML,DLの各技法の中では、いかに簡単に計算するか、計算を省略するかなどが重大な関心事項である。最初はなぜ計算の省力化にそんなに熱心なことが腑に落ちなかったが、MLやDLで扱う数字(パラメータ)は100や1,000などの普段の生活で使うような数字ではなく、数千万以上となることもあり、現在簡単に扱えるコンピュータの性能をはるかに超える計算量となってしまうことや、計算できても数日間待たないといけない(答えを知りたいときに使えない)とことを学び合点がいった。このような省力化にも行列とベクトルを活用することで可能となる。多くの方程式をまとめて扱うにはベクトル、行列(さらに一般化した概念であるテンソル(Tensor))の計算で行える。
(2)固有値・固有ベクトル・固有値分解
●ある行列Aに対して特殊なベクトルv(両辺)と係数λ(右辺)がある。
このとき、
$Av =λv$
が成り立つ特殊なベクトルvを行列Aに対する固有ベクトル、
係数λを行列Aに対する固有値という。
(固有値・固有ベクトルのイメージ)
上記の定義だけで固有値・固有ベクトルとは何かというイメージが湧かないが、任意の行列Aに対して拡大又は縮小のみが作用されるベクトルのことを固有ベクトル、拡大・縮小率のことが固有値である、という説明は非常にイメージがしやすい。(「ゼロから作るPython機械学習」八谷大岳)
●正方行列Aが固有値λ及び固有ベクトルvをもつとき、正方行列Aは以下の固有値と固有ベクトルの積に分解できる。この分解を固有値分解という。
$A=VΛV^(-1)$
行列Λは固有値を対角成分に並べた正方行列である。
固有値分解のイメージは、中学数学でも出てくる素因数分解を行列に対して行うようなものである。行列の構造が見えやすくなり、行列の累乗の計算が容易になる。
(3)特異値分解
●固有値分解は正方行列(m×m行列)だけに使えるツールであるが、より一般化し、正方行列以外の行列(m×n行列)も使えるツールが、特異値分解である。
●任意の零行列ではないm×n行列Aに対して、
$Av=σu$, $A^⊤ v=σv$
を満たすような正の数σを特異値、m次元ベクトルuを左特異ベクトル、n次元ベクトルvを右特異ベクトルという。
●定義式から、$AA^⊤ u=σ^2 u$,$A^⊤ Av=σ^2 v$が得られるので、行列$AA^⊤$と$A^⊤ A$の固有値・固有ベクトルを求めることで、行列Aの特異値と(左右)特異ベクトルが分かる。このようにして求められた特異値を大きい順に(i,i)で成分に並べ、そのほかの成分を0で埋めたm×n行列Σと、左特異ベクトルを列として横に並べたm次正方行列U、右特異ベクトルを列をして並べたn次正方行列Vを用いて、
$A=UΣV^⊤$
の形で表わすことを、Aの特異値分解という。
このとき、特異値を降順に並べるとΣは一意に定まるが、U及びVは一意には定まらない。
3.確率・統計
(1)確率・統計とML,DL
●多くのML、DLのタスクにおいては、観測したデータの背後にある法則を見つけ、将来の予測をすることが大きな目的となっている。その法則を見つける際に、どの程度それが起きやすいかを計算する上で不可欠となるツールが確率・統計である。
(2)確率変数
●確率・統計の学習のほか、ML,DLにおいても頻繁に確率変数という用語が出てくるがこの概念が捉えづらいが、**”「事象」を「数値」に変換する関数”**という説明はイメージが湧いて非常に分かりやすい。
ある対象としている現象の中で、様々な事象があり得るとき、それぞれの事象ごとに、それが「どの程度起きそうか」という度合いを考えます。確率とはその度合いのこととします。そして、その確率に従って、色々な値をとりうる確率変数(random variable)を考えます。確率変数は、名前に「変数」とついていますが、「事象」を「数値」に変換する関数と考えると理解しやすくなります。例えば、「コインを投げて表が出る」という「事象」を、「1」という「数値」に変換し、「コインを投げて裏が出る」という「事象」を、「0」という「数値」に変換する関数を考えると、これは「1」か「0」という値のどちらかをとりうる確率変数だ(注釈1)ということになります。
https://tutorials.chainer.org/ja/06_Basics_of_Probability_Statistics.html
(3)条件付き確率
●ある条件下で着目した事象の確率を考えること。
ある事象X=xが与えられた下で、Y=yとなる確率であり、例えば、雨が降っている条件(X)下で、交通事故に遭う確率(Y)などのことである。
$P(Y=y∣X=x)=P(Y=y,X=x)/P(X=x)$
(4)ベイズの定理
●ベイズ論は確率・統計のコンテンツの1分野として出てくると非常に混乱してしまう。確率・統計に対する見方・考え方の前提となっている考え方が通常習うものとそもそも異なっているからである。つまり、
・実証で得られたデータのみを活用する頻度論(通常習う確率・統計)
・過去のデータや事前知識を推定結果に反映させるベイズ論
という前提をまず理解しておく必要がある。
●このベイズ論は、データが少ない場合でも活用できること、学習能力があることから、ML,DLにおいて広く活用されている。
ベイズ統計学では最初に確率を設定しておき、情報が入るたびに、”その時点での確率”を変更していきます。つまり、現時点でなんのデータもなかったとしても、とりあえず確率を設定しておくことができるのです。事前確率を設定した段階から、何か新たな情報をゲットして、事後確率を更新していきます。そして、また新たな情報を手に入れたら、前回は事後確率だったものが事前確率となって、さらに確率の更新が行われるという仕組みです。このようにベイズ統計学の考え方には、いわば学習能力があるということです。
https://ai-trend.jp/basic-study/basic/bayesian-statistics/
●ベイズの定理
事象の結果Xが生じたという前提の下で、原因がYである確率を求めることができる。
$P(Y=y∣X=x)=P(X=x|Y=y)P(Y=y)/P(X=x)$
●ベイズの定理には事象の確率という考え方を採用する特徴があり、応用例としては迷惑メールのふるい分けにも利用されている。
(5)分布総論
●分布を学ぶ際、いきなりベルヌーイの式などから入ると頭がごちゃごちゃになりやすい。まず最初に下記の図で、ベルヌーイ分布、二項分布、カテゴリカル分布、多項分布の関係を頭に入れてから各論に入ると理解しやすい。
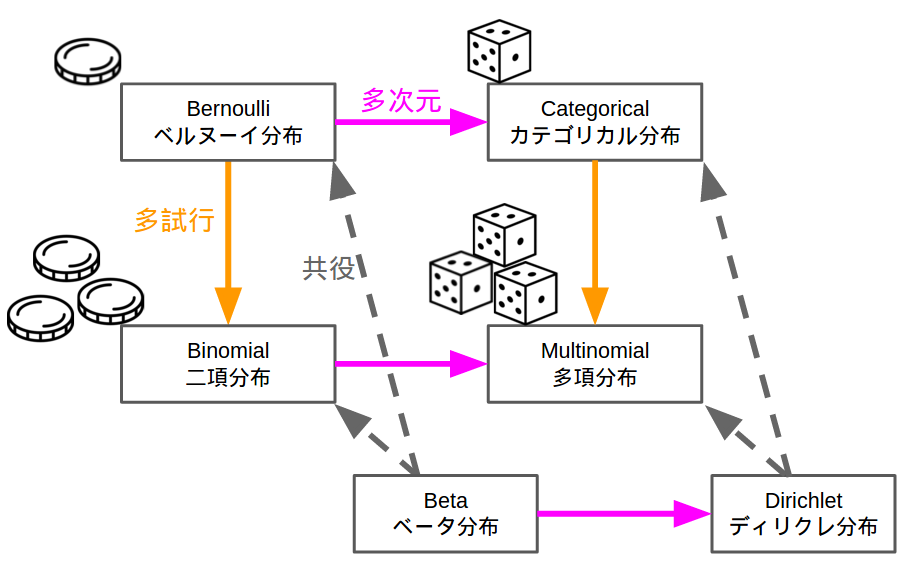
https://machine-learning.hatenablog.com/entry/2016/03/26/211106
(6)ベルヌーイ分布
●「コインを投げた結果が表か裏か」のように2種類の結果しか得られないような試行のことをベルヌーイ試行という。ベルヌーイ分布はすべての分布の基本である。
●1回のベルヌーイ試行によって得られる確率分布がベルヌーイ分布である。確率関数のパラメータ(確率分布を特徴づける値)は一方の結果の生起確率p。
・確率変数 $X=0,1$(表なら1,裏なら0)
・確率関数 $P(X=x)=p^x(1-p)^(1-x)$
・パラメータ 表が出る確率 $P=0.5$
・期待値 $E(X)=μ$
・分散 $V(X)=μ(1−μ)$
(7)マルチヌーイ分布(カテゴリカル分布)
●ベルヌーイ分布の多次元版。3つ以上の値のモデリングに用いるのに適した分布である。(サイコロを転がし、1-6までの値のモデルを行うことが典型的な例。)
●k次元のワンホットベクトル(ベクトルxの成分のうち、ただ1つが1であり、そのほか全てが0であるベクトル)で構成されるデータD={x_1,….,x_n}がマルチヌーイ分布
math
$f(x;p)=∏ p_j^(x_j)$
ただし、$∑p_j =1,0≤p_j≤1,j=1,…,k$
4.情報理論
(1)情報量
●情報量、エントロピー、交差エントロピー、KLダイバージェンス等の式を似たような形が多く、覚えてさえおけばさしあたり問題は解ける。ただ、何をしているのかという意味を理解しておかないと、なぜ情報量やエントロピーでは式にマイナスをつけるのかが分からなくなる。
●情報量とは以下のことを意味する。
・発生する確率が低いこと(珍しいこと)が分かった時のほうが、情報量が多い
関数$f(x)=log_2x$が単調減少であることから秋からに満たされている。
・情報量は足し算で増えていく。複数の事象が発生する確率は積で表現されるが、情報量においては和で表現したい。
●あることが分かった際の「そのことの情報量」を自己情報量と呼ぶ。
$i(x)=-log_2P(x)$
※対数の底には2を採用することが一般的だが1より大きな実数であれば定数倍を除いて本質的に影響はない
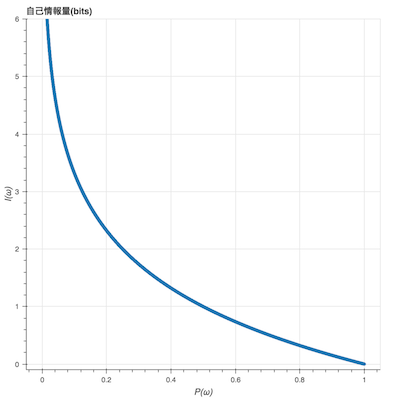
●自己情報量の式ではなぜlogの前に「-」(マイナス)をつけるのか。通常のlogを描くと右肩上がりのグラフになり、珍しいものほど大きい数で表わしたいという考え方とは合わなくなる。このため、マイナスをつけて上記のような右肩下がりとして、情報量を扱いやすくしている。
(2)エントロピー
●平均情報量(エントロピー)は、その情報源がどれだけ情報を出しているかを測る尺度である。その情報が不規則であればあるほど平均として多くの情報を運んでいることを意味する。
「わからなさ」あるいは「不確実性」のことを、専門用語で「情報エントロピー」と呼びます。
そして、「わからなさ」は「新たに何か分かった時の平均情報量」と等しくなります。
よって、情報エントロピー = 平均情報量 として定義されます。
https://logics-of-blue.com/information-theory-basic/
●シャノン氏は、あらゆる事象が全て同じ確率で起こる場合に不確実性の高さを最大とした。これを表す尺度としてHがある。多くの情報量理論で用いられている基本的な定理である。
●離散確率変数Xにおいて、$X=x$となる確率が$p(x)$で与えられているときに確率変数Xのエントロピーは、
平均情報量 $H(X)=-∑_x p(x) log_2p(x)$
と定義される。エントロピー(平均情報量)は、情報量(すなわち、事象の起こりにくさ、珍しさ)の期待値で示される。そのため、確率変数のランダム性の指標としてよく用いられる。
(3)交差エントロピー
●**交差エントロピー(Cross Entropy)**は2つの確率分布の差を表す尺度である。主にニューラルネットワークのクラス分類等に用いられている。
●基本的にはKLダイバージェンスと同じ尺度を提供している。
●2つの確率分布p(x)とq(x)があるとき、交差エントロピーは以下の式で表わされる。
$H(p,q)=-∑_x p(x) log_2q(x)$
pがデータによって近似される真の分布でありqがモデルの分布。pとqは非対称であることに注意。
●交差エントロピーは、分類問題を解くための損失関数としてよく用いられるが、2つの確率分布が全く同じ時に交差エントロピーが最小となる性質を利用したもの。
●ML,DLにおける損失関数としては二乗誤差が有名だが、分類問題を扱う際には交差エントロピーが頻繁に使われる。その理由は、教師データと学習結果が大きく乖離している(損失関数の値が大きい)場合に、交差エントロピーを使った方が損失関数よりも学習あたりの学習スピードが早いからである。
●ちなみになぜ「交差」という名前なのかであるが、$plog(p)$のようにlogの内と外に同じ変数が使われているのが普通のエントロピーであるのに対して$tlogy$のようにlogの内と外で異なる変数が使われているため、"交差"エントロピーと呼ぶ。
(4)KLダイバージェンス
●KLダイバージェンス(Kullback-Leibler divergence)は2つの確率分布の近さを表現する最も基本的な量で、統計学・情報理論において非常に重要な役割を果たす。
●2つの確率分布$p(x)$と$q(x)$に対して、式
$D(p∥q)=∑_xp(x) log_2 (p(x)/q(x))$
で定義される量がKLダイバージェンス。
●KLダイバージェンスには使い勝手のいい性質がいくつかある。一つは非負性でありどのようなP,Qに対しても非負(ゼロ以上)の値となる。PとQが同じ分布となる場合にのみKLダイバージェンスは0となる。
●ただ、KLダイバージェンスは対称性がない(PとQを交換したら等価でない)ため、pから見たqとqから見たpで別の値となる。このため、$D_KL (p∥q)$と$D_KL (q∥p)$は同じ値ではなく、どちらを使うかは重要な選択となる。
参考文献
●JDLA E資格シラバス最新版(2020)
https://www.jdla.org/wp-content/uploads/2019/09/JDLA_E%E3%82%B7%E3%83%A9%E3%83%90%E3%82%B9_2020%E7%89%88.pdf
●「統計学入門」(東京大学教養学部統計学教室編・東京大学出版会)
●「情報 第2版」(山口和紀・東京大学出版会)
●「深層学習」(Ian Goodfellow,Yoshua Bengio,Aaron Courville,2016)
●「ゼロからつくるPyhon機械学習プログラミング入門」(八谷大岳・講談社)
●「徹底攻略ディープラーニングE資格問題集 第2版」(インプレス)