四元数に引き続き八元数を作ります。複雑な八元数の積をなるべく少ないルールで導出します。最後に考え方をプログラムで表現します。
関連する亜種も見ます。
シリーズの記事です。
- 多項式の積を計算
- 外積と愉快な仲間たち
- ユークリッド空間のホッジ双対とバブルソート
- 四元数を作ろう
- 四元数と行列で見る内積と外積の「内」と「外」
- 八元数を作ろう ← この記事
- 八元数の積をプログラムで確認
- 外積の成分をプログラムで確認
- 多元数の積の構成
- 十六元数を作ろう
関連するコードをまとめたリポジトリです。
この記事には関連記事があります。
- 2017.12.04 八元数と7次元の外積 ← お勧め
- 2017.03.14 表現行列で考える四元数
- 2017.03.25 クリフォード代数で考えるパウリ行列と双四元数
双四元数
複素数 $\mathbb{C}$ の係数に複素数を入れることで双複素数 $\mathbb{C}⊗\mathbb{C}$ を作りましたが、同じように複素数の係数に四元数 $\mathbb{H}$ を入れることで双四元数 $\mathbb{C}⊗\mathbb{H}$ が作れます。
※ 四元数の中に四元数を入れた $\mathbb{H}⊗\mathbb{H}$ ではありません。
新たに外側の虚数 $h$ を追加します。係数が増えすぎて混乱するため添え字で表します。
\begin{align}
&(a_1+a_2i+a_3j+a_4k)+(a_5+a_6i+a_7j+a_8k)h \\
&=a_1+a_2i+a_3j+a_4k+a_5h+a_6ih+a_7jh+a_8kh \\
&=a_1+a_2i+a_3j+a_4k+a_5h+a_6hi+a_7hj+a_8hk
\end{align}
双四元数において $i,j,k$ と $h$ は同列の存在ではなく、$h$ は係数の一部として扱います。通常の複素数を用いた式 $2ix$ で $x$ の係数が $2i$ であるのと同じように、$2hj$ で $j$ の係数が $2h$ だと考えます。そのため $h$ は自由に動かすことができます($2hj=2jh$)。この考え方を反映して $h$ を係数に含めています。
元の計算規則
$i,j,k$ の積は通常の四元数と同じです。
i^2=j^2=k^2=ijk=-1 \\
ij=-ji=k,\ jk=-kj=i,\ ki=-ik=j
$h$ が絡んだ場合、$h$ は係数の一部として計算します。
\begin{align}
h^2&=-1 \\
(hi)^2&=(hh)(ii)=(-1)(-1)=1 \\
(hj)^2&=(hh)(jj)=(-1)(-1)=1 \\
(hk)^2&=(hh)(kk)=(-1)(-1)=1 \\
(hi)(hj)&=(hh)(ij)=(-1)(k)=-k \\
(hj)(hi)&=(hh)(ji)=(-1)(-k)=k \\
(hj)(hk)&=(hh)(jk)=(-1)(i)=-i \\
(hk)(hj)&=(hh)(kj)=(-1)(-i)=i \\
(hk)(hi)&=(hh)(ki)=(-1)(j)=-j \\
(hi)(hk)&=(hh)(ik)=(-1)(-j)=j \\
\end{align}
元の積が閉じていることから一般の積も閉じています。計算は複雑なため省略しますが、興味があれば確認してみると良いでしょう。
ローレンツ変換との関係
双四元数から $1,hi,hj,hk$ を取り出せば、ノルムは $+,-,-,-$ 型になります。
\begin{align}
&\{a+b(hi)+c(hj)+d(hk)\}^*\{a+b(hi)+c(hj)+d(hk)\} \\
&=\{a-b(hi)-c(hj)-d(hk)\}\{a+b(hi)+c(hj)+d(hk)\} \\
&=a\{a+b(hi)+c(hj)+d(hk)\} \\
&\quad -b(hi)\{a+b(hi)+c(hj)+d(hk)\} \\
&\quad -c(hj)\{a+b(hi)+c(hj)+d(hk)\} \\
&\quad -d(hk)\{a+b(hi)+c(hj)+d(hk)\} \\
&=aa+ab(hi)+ac(hj)+ad(hk) \\
&\quad -ba(hi)-bb\underbrace{(hi)(hi)}_{1}-bc\underbrace{(hi)(hj)}_{-k}-bd\underbrace{(hi)(hk)}_{j} \\
&\quad -ca(hj)-cb\underbrace{(hj)(hi)}_{k}-cc\underbrace{(hj)(hj)}_{1}-cd\underbrace{(hj)(hk)}_{-i} \\
&\quad -da(hk)-db\underbrace{(hk)(hi)}_{-j}-dc\underbrace{(hk)(hj)}_{i}-dd\underbrace{(hk)(hk)}_{1} \\
&=a^2-b^2-c^2-d^2
\end{align}
この性質を利用して、ローレンツ変換の計算に使うことができます。参考までに同等の理論について述べた文献を示します。
なお、積の計算過程で $(hi)(hj)=-k$ のように $h$ が付かない元が現れていますが、$hh$ をそれ以上計算しなければ元に $h$ を残すことができます。
(hi)(hj)=(hh)(ij)=h(hk)
パウリ行列との関係
量子力学のスピンで使われるパウリ行列という行列があります。
σ_1=\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right),
σ_2=\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right),
σ_3=\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)
※ $σ_1$と$σ_3$は対称行列(転置すると元に戻る行列)、$σ_2$はエルミート行列(複素共役を取って転置すると元に戻る行列・自己随伴行列)です。実行列では共役が無意味なことから、実対称行列はエルミート行列の特殊な形です。
双四元数から $1,hi,hj,hk$ を取り出したものはパウリ行列と同型です。
\{1,hi,hj,hk\}≅\{I,σ_1,σ_2,σ_3\}
$(hi)^2=(hj)^2=(hk)^2=1$ に対応する関係として、パウリ行列を2乗すると単位行列になります。
\underbrace{\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)^2}_{σ_1^2}
=\underbrace{\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right)^2}_{σ_2^2}
=\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)^2}_{σ_3^2}
=\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right)}_{I}
双四元数での係数の $h$ は、パウリ行列では $i$ として表れます。
(hi)(hj)=h(hk)\ ↦\ σ_1σ_2=iσ_3
ところで $hi$ に $-h$ を掛ければ $h$ を取り除けます。
\underbrace{-h}_{-i}\underbrace{(hi)}_{σ_1}=-(hh)i=i
この関係を使えば四元数とパウリ行列の同型対応が分かります。
\{1,i,j,k\}≅\{I,-iσ_1,-iσ_2,-iσ_3\}
表現行列
パウリ行列を使えば、双四元数や四元数を行列で表現できます。
双四元数の表現行列を確認します。
\begin{align}
&a+bhi+chj+dhk \\
&↦aI+bσ_1+cσ_2+dσ_3 \\
&=a\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right)}_{1}
+b\underbrace{\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)}_{hi}
+c\underbrace{\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right)}_{hj}
+d\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)}_{hk} \\
&=\left(\begin{matrix}a & 0 \\ 0 & a\end{matrix}\right)
+\left(\begin{matrix}0 & b \\ b & 0\end{matrix}\right)
+\left(\begin{matrix}0 & -ci \\ ci & 0\end{matrix}\right)
+\left(\begin{matrix}d & 0 \\ 0 & -d\end{matrix}\right) \\
&=\left(\begin{matrix}a+d & b-ci \\ b+ci & a-d\end{matrix}\right)
\end{align}
※ エルミート行列であるパウリ行列(と単位行列)から構成されていることから、双四元数の表現行列はエルミート行列です。
四元数の表現行列を確認します。
\begin{align}
&a+bi+cj+dk \\
&↦aI+b(-iσ_1)+c(-iσ_2)+d(-iσ_3) \\
&=a \underbrace{\left(\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right)}_{I}
+b(-i)\underbrace{\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)}_{σ_1}
+c(-i)\underbrace{\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right)}_{σ_2}
+d(-i)\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)}_{σ_3} \\
&=a\underbrace{\left(\begin{matrix} 1 & 0 \\ 0 & 1\end{matrix}\right)}_{1}
+b\underbrace{\left(\begin{matrix} 0 & -i \\ -i & 0\end{matrix}\right)}_{i}
+c\underbrace{\left(\begin{matrix} 0 & -1 \\ 1 & 0\end{matrix}\right)}_{j}
+d\underbrace{\left(\begin{matrix}-i & 0 \\ 0 & i\end{matrix}\right)}_{k} \\
&=\left(\begin{matrix} a & 0 \\ 0 & a \end{matrix}\right)
+\left(\begin{matrix} 0 & -bi \\ -bi & 0 \end{matrix}\right)
+\left(\begin{matrix} 0 & -c \\ c & 0 \end{matrix}\right)
+\left(\begin{matrix}-di & 0 \\ 0 & di\end{matrix}\right) \\
&=\left(\begin{matrix}a-di & -(c+bi) \\ c-bi & a+di\end{matrix}\right)
\end{align}
※ エルミート行列ではありません。$a=0$ であれば歪エルミート行列になります。$j$ の表現行列が複素数の $i$ の表現行列と一致するのは、ケーリー=ディクソン構成を反映しています。
行列式
四元数の表現行列には共役が現れています。
$α=a-di,\ β=-(c+bi)$ とおけば
\begin{align}
\left(\begin{matrix}a-di & -(c+bi) \\ c-bi & a+di\end{matrix}\right)
&=\left(\begin{matrix}α & β \\ -β^* & α^* \end{matrix}\right)
\end{align}
このことから、行列式がノルムの2乗になることが分かります。(ユークリッドノルム)
\begin{align}
\left|\begin{matrix}α & β \\ -β^* & α^* \end{matrix}\right|
&=αα^* +ββ^* \\
&=(a-di)(a+di)+(c+bi)(c-bi) \\
&=(a^2+d^2)+(c^2+b^2) \\
&=a^2+b^2+c^2+d^2
\end{align}
双四元数でも行列式がノルムの2乗となります。(ミンコフスキーノルム)
\begin{align}
\left|\begin{matrix}a+d & b-ci \\ b+ci & a-d\end{matrix}\right|
&=(a+d)(a-d)-(b-ci)(b+ci) \\
&=(a^2-d^2)-(b^2+c^2) \\
&=a^2-b^2-c^2-d^2
\end{align}
記憶法
パウリ行列を覚えるためのコツを書きます。
※ ここで述べることが分かりやすいかは人によりますので、各自工夫してみてください。
双四元数の表現行列の第1列は $a$ からU字型に $b, ci, d$ と並んでいます。
\left(\begin{matrix}a+d \\ b+ci\end{matrix}\right)
※ $i$ は $c$ にだけ付きます。対称性につられて $d$ に $i$ を付けないように注意してください。
第2列は、行列式からミンコフスキーノルム($a^2-b^2-c^2-d^2$)が求まるように決めます。行列式はたすきがけするため第1列の成分を上下入れ替えて、交差項が出ないように後ろの項をマイナスにします。
\left(\begin{array}{c|c}a+d & b-ci \\ b+ci & a-d\end{array}\right)
これを $a,b,c,d$ で分解すれば、単位行列とパウリ行列が得られます。
\begin{align}
&\left(\begin{matrix}a+d & b-ci \\ b+ci & a-d\end{matrix}\right) \\
&=a\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right)}_{I}
+b\underbrace{\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)}_{σ_1}
+c\underbrace{\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right)}_{σ_2}
+d\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)}_{σ_3}
\end{align}
※ $σ_2,σ_3$ の第2列がマイナスになっているのは、交差項を抑制したことと関係あることが分かります。
任意性
同型対応は演算の結果が一致すれば良いので任意性があります。例えば四元数の演算規則には巡回性があるため、対応関係を巡回的にずらしても成り立ちます。
巡回性以外にも、例えば次のような同型対応も可能です。
\{1,i,j,k\}≅\{I,iσ_3,iσ_2,iσ_1\}
同型対応を変えれば表現行列も変わります。この対応で表現行列を求めれば、ケーリー=ディクソン構成と共役がきれいに表れます。
\begin{align}
α+βj
&=(a+bi)+(c+di)j \\
&=a+bi+cj+dk \\
&↦aI+b(iσ_3)+c(iσ_2)+d(iσ_1) \\
&=a \underbrace{\left(\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right)}_{I}
+bi\underbrace{\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)}_{σ_3}
+ci\underbrace{\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right)}_{σ_2}
+di\underbrace{\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)}_{σ_1} \\
&=a\underbrace{\left(\begin{matrix} 1 & 0 \\ 0 & 1\end{matrix}\right)}_{1}
+b\underbrace{\left(\begin{matrix} i & 0 \\ 0 & -i\end{matrix}\right)}_{i}
+c\underbrace{\left(\begin{matrix} 0 & 1 \\ -1 & 0\end{matrix}\right)}_{j}
+d\underbrace{\left(\begin{matrix} 0 & i \\ i & 0\end{matrix}\right)}_{k} \\
&=\left(\begin{matrix}a & 0 \\ 0 & a \end{matrix}\right)
+\left(\begin{matrix}bi & 0 \\ 0 & -bi\end{matrix}\right)
+\left(\begin{matrix}0 & c \\ -c & 0 \end{matrix}\right)
+\left(\begin{matrix}0 & di \\ di & 0 \end{matrix}\right) \\
&=\left(\begin{matrix}a+bi & c+di \\ -(c-di) & a-bi\end{matrix}\right) \\
&=\left(\begin{matrix}α & β \\ -β^* & α^* \end{matrix}\right)
\end{align}
行列の形を見れば、行列式がノルムの2乗になるのは一目瞭然です。
\left|\begin{matrix}α & β \\ -β^* & α^* \end{matrix}\right|
=αα^* + ββ^*
=a^2+b^2+c^2+d^2
参考
四元数の表現行列やパウリ行列との関係は以下の書籍を参考にしました。
以下の資料では四元数とパウリ行列によって8次元空間(双四元数によって表されるのと同じ空間)が構成されることや、表現行列の求め方が詳しく説明されています。
双曲四元数
ローレンツ変換が扱えて、元同士の積で $h$ が出て来ないように元を定義し直したのが双曲四元数です。
人為的に定義を調整しているため、双四元数のサブセットではありません。その調整の代償として結合性が失われています。
【例】 $(ii)j≠i(ij)$
\begin{align}
(ii)j&=j \\
i(ij)&=ik=-j
\end{align}
双曲四元数についての詳細は四元数を作ろうを参照してください。
参考
分配多元環 - Wikipediaには次のような記述があります。
R 上の双曲四元数環は、特殊相対論にミンコフスキー空間が用いられるようになる以前に経験的に用いられていた。
双四元数と双曲四元数でローレンツ変換を扱うことについて、次のような見解があります。ここに出て来る複四元数は、この記事での双四元数と同じものを指します。
168 NS 2015/12/12 (土) 12:32:20 ID:ATxOZThXXM
四元数とミンコフスキー空間について調べてみました。
普通の四元数はユークリッド空間ですが、ミンコフスキー空間の四元数としては次の二つが考えられます。
①複四元数(biquaternion)
ハミルトンは四元数を発表した翌1844年に複四元数を発表しました。
普通の四元数は各要素が実数ですが、各要素を複素数とする四元数です。
時間を実数とし、空間を純虚数とすると4次元ミンコフスキー空間になります。時間が純虚数、空間が実数でも同様です。
②双曲四元数(hyperbolic quaternion)
スコットランドのマクファーレンは1890年代に双曲四元数を発表しました。
二乗して-1になる普通の虚数単位でなく、二乗して1になる三つの虚数単位を実数に加えたものです。
この奇妙な虚数単位は直線y=xについての対称移動を表していて、1848年にイングランドのクックルが考案しました。
これでもミンコフスキー空間を作れますが、双曲四元数はとても不便な数です。乗法の結合法則が成立せず、(ij)j≠i(jj)のようにalternativeでもないので十六元数並みです。
現代では①の説明がされることが多いようです。
分解型四元数
双複素数の一部から分解型複素数を作ったのと同じように、双四元数の一部から分解型四元数が作られます。
分解型はノルムの2乗の符号が真ん中で分離されることを意味するため、$(+,+,-,-)$ 型となるように元を選んで文字を付け替えます。
\begin{align}
\{1,i,hj,hk\} &≅ \{1,i,j,k\} \\
a+bi+chj+dhk &↦ a+bi+cj+dk
\end{align}
なぜ元をこう選んだのかは、ノルムを計算した後で考察します。
元の計算規則
双四元数→分解型四元数の対比により、元の計算規則を確認します。
\begin{align}
i^2&=-1& &↦& i^2&=-1 \\
(hj)^2&=1& &↦& j^2&=1 \\
(hk)^2&=1& &↦& k^2&=1 \\
i(hj)&=hk& &↦& ij&=k \\
(hj)i&=-hk& &↦& ji&=-k \\
(hj)(hk)&=-i& &↦& jk&=-i \\
(hk)(hj)&=i& &↦& kj&=i \\
(hk)i&=hj& &↦& ki&=j \\
i(hk)&=-hj& &↦& ik&=-j
\end{align}
うまく閉じていることが分かります。元の積が閉じていることから、一般の積についても閉じています。
共役
共役は通常の四元数と同様に虚部の符号反転です。
(a+bi+cj+dk)^*=a-bi-cj-dk
ノルム
ノルムの2乗を計算すれば $(+,+,-,-)$ 型となることが確認できます。
\begin{align}
&(a+bi+cj+dk)^*(a+bi+cj+dk) \\
&=(a-bi-cj-dk)(a+bi+cj+dk) \\
&=a(a+bi+cj+dk) \\
&\quad -bi(a+bi+cj+dk) \\
&\quad -cj(a+bi+cj+dk) \\
&\quad -dk(a+bi+cj+dk) \\
&=aa+abi+acj+adk \\
&\quad -bai-bb\underbrace{ii}_{-1}-bc\underbrace{ij}_{k}-bd\underbrace{ik}_{-j} \\
&\quad -caj-cb\underbrace{ji}_{-k}-cc\underbrace{jj}_{1}-cd\underbrace{jk}_{-i} \\
&\quad -dak-db\underbrace{ki}_{j}-dc\underbrace{kj}_{i}-dd\underbrace{kk}_{1} \\
&=a^2+b^2-c^2-d^2
\end{align}
元 $1,i,j,k$ の2乗は $1,-1,1,1$ ですが、ノルムの2乗の符号 $(+,+,-,-)$ とは一致しません。元の2乗の符号を $+,-,+,+$ と表して2番目以降の符号を反転させれば、ノルムの2乗の符号と一致します。ノルムの2乗が $a^2-b^2i^2-c^2j^2-d^2k^2$ であることを考えれば、この関係はすぐ分かるでしょう。
八元数
いよいよラスボスの八元数です。
構成方法は双四元数と同じです。
\begin{align}
&(a_1+a_2i+a_3j+a_4k)+(a_5+a_6i+a_7j+a_8k)h \\
&=a_1+a_2i+a_3j+a_4k+a_5h+a_6ih+a_7jh+a_8kh \\
&=a_1+a_2i+a_3j+a_4k+a_5h+a_6i_h+a_7j_h+a_8k_h
\end{align}
双四元数では $h$ を係数として扱いましたが、八元数では $i,j,k$ と同列な元として扱う点が異なります。$ih,jh,kh$ は一塊の元のため、ここでは $i_h,j_h,k_h$ と表記します。これは一般的な表記ではありませんが、次のように元が直感的に構成できます。
ih=i_h,\ jh=j_h,\ kh=k_h
※ 元の表記方法はいくつか流儀があります。Wikipediaでは $e_0,...,e_7$ のように添字で表しています。添字表記では計算ルールを四元数から推測することが難しくなるため、この記事では採用していません。
【例】 $ij=k,\ ih=i_h\ ⇔\ e_1e_2=e_3,\ e_1e_4=e_5$
計算規則
虚数の元は2乗が $-1$ になると定義します。
i^2=j^2=k^2=h^2=i_h^2=j_h^2=k_h^2=-1
※ 双四元数では $(ih)^2=(jh)^2=(kh)^2=1$ となるため異なります。
$i,j,k$ の積は通常の四元数と同じです。
ij=-ji=k,\ jk=-kj=i,\ ki=-ik=j
$h$ も元の1つのため、$i,j,k$ と同じように反交換性を持ちます。
ih=-hi=i_h,\ jh=-hj=j_h,\ kh=-hk=k_h
これだけでは演算が一意に決まりません。任意性がありますが、標準的には $ij_h=-k_h$ と定義します。
※ このように定義すれば、虚部で表される7次元空間を構成する3次元の部分空間が右手系に統一できるという意図があるようです。部分空間については外積やファノ平面などを考える必要があります。詳細は機会があればまとめる予定です。
異なる元の積には巡回性と反交換性が成り立ちます。(同じなら $-1$)
反結合性
$ij_h=-k_h$ をベースに演算を組み立てると、次のような性質が現れます。
$h$ が結合した元 $i_h, j_h, k_h$ は、構成する $ih, jh, kh$ を分解して隣接する元と結合する際に符号が反転します。これを反結合性と呼びます。
i(jh)=-(ij)h
結合法則が成り立たないため $ijh$ のように括弧を省略することはできません。混乱を避けるため、八元数の計算では連続した掛け算では常に括弧を付けます。
いくつか例を示します。
\begin{align}
ij_h&=\underbrace{i(jh)}_{-(ij)h}=-\underbrace{(ij)}_{k}h=-k_h \\
i_hj&=\underbrace{(ih)j}_{-i(hj)}=-i\underbrace{(hj)}_{-jh}=ij_h=-k_h
\end{align}
$i_hj=ij_h$ より $h$ の位置が動いていると解釈できます。反交換性からも同じ結果になります。
i_hj=-ji_h=-\underbrace{j(ih)}_{-(ji)h}=\underbrace{(ji)}_{-k}h=-k_h
例外
反結合性の例外として、同じ元が隣接した場合は符号の反転なしで結合して $-1$ となります。同じ元同士は結び付きが強いと解釈できます。これを交代結合性と呼びます。
\begin{align}
【例】\
ii_h&=\underbrace{i(i}_{-1}h)=-h \\
i_hh&=(i\underbrace{h)h}_{-1}=-i \\
i_hj_h&=\underbrace{(ih)(jh)}_{X(jh)=-(Xj)h}=-\{\underbrace{(ih)j}_{-kh}\}h=(k\underbrace{h)h}_{-1}=-k
\end{align}
奇妙な規則ですが、巡回性(①②=③ → ②③=① → ③①=②)に由来します。
ih=i_h\ →\ hi_h=i\ →\ i_hi=h
これらに反交換性を適用すれば、先ほど見た関係が得られます。
i_hh=-i,\ ii_h=-h
$i_hj_h=-k$ は複雑ですが $(ij)(hh)=-k$ と覚えれば簡単でしょう。$ij_h=i_hj=-k_h$ と符号が同じ($-k$)なのも意識すると良いかもしれません。
※ ここでも巡回性は成り立っているため $ki_h=-j_h$ から $i_hj_h=-k$ が得られます。
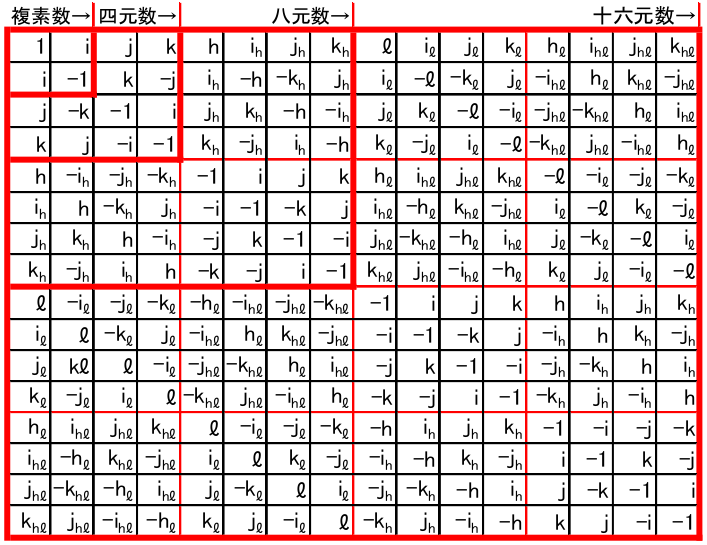
乗積表
まとめとして乗積表を掲載します。
※ 表を覚えるよりも、反結合性と例外に基づいて個々の結果を直接導くことをお勧めします。その過程をプログラムで表現したものを最後に掲載します。
読み方は、1行目と1列目が見出しで「縦×横」に拾います。(例: 3行($j$)4列($k$)=$i$)
| $1$ | $i$ | $j$ | $k$ | $h$ | $i_h$ | $j_h$ | $k_h$ |
|---|---|---|---|---|---|---|---|
| $i$ | $−1$ | $k$ | $−j$ | $i_h$ | $−h$ | $−k_h$ | $j_h$ |
| $j$ | $−k$ | $−1$ | $i$ | $j_h$ | $k_h$ | $−h$ | $−i_h$ |
| $k$ | $j$ | $−i$ | $−1$ | $k_h$ | $−j_h$ | $i_h$ | $−h$ |
| $h$ | $−i_h$ | $−j_h$ | $−k_h$ | $−1$ | $i$ | $j$ | $k$ |
| $i_h$ | $h$ | $−k_h$ | $j_h$ | $−i$ | $−1$ | $−k$ | $j$ |
| $j_h$ | $k_h$ | $h$ | $−i_h$ | $−j$ | $k$ | $−1$ | $−i$ |
| $k_h$ | $−j_h$ | $i_h$ | $h$ | $−k$ | $−j$ | $i$ | $−1$ |
※ この乗積表はWikipediaと同じ並べ方です。元の表記を置換すれば一致します。
見出しの1行目と1列目を除いて考えれば、対角成分は元の2乗で $-1$、それ以外の非対角成分は反交換性により反対称です(左図)。局所的な3×3の領域にも同様の反対称性があります(右図)。
※ 右図の①と④は非対角成分の符号が逆で、②と③は一致します。④は②(③)から$_h$を取り除いた形です。
多元数は複素数から出発して、ケーリー=ディクソン構成を適用するごとに拡張されます。複素数→四元数→八元数は上位互換での拡張となっており、下位の乗積表をそのまま含みます。参考までに十六元数までの乗積表を示します。
※ 十六元数についての詳細は、続編の十六元数を作ろうを参照してください。
結合法則
$h$ が関係する組み合わせでは反結合性が現れるため、結合法則を満たしません。
結合法則を満たす: $(ij)k=i(jk)$
\begin{align}
(ij)k&=kk=-1 \\
i(jk)&=ii=-1
\end{align}
結合法則を満たさない: $(i_hj_h)k_h=-i_h(j_hk_h)$ (反結合)
\begin{align}
(i_hj_h)k_h&=(-k)k_h=h \\
i_h(j_hk_h)&=i_h(-i)=ii_h=-h
\end{align}
四元数では交換法則、八元数では結合法則を失います。十六元数はもっと不便になります。ここでは詳細には触れませんが、興味があれば調べてみると良いでしょう。
積
四元数の虚部が3次元ベクトルと同一視できるように、八元数の虚部は7次元ベクトルと同一視できます。
\vec{v}=\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\\x_5\\x_6\\x_7\end{matrix}\right)=x_1i+x_2j+x_3k+x_4h+x_5i_h+x_6j_h+x_7k_h
八元数で表した7次元ベクトルの積を計算すれば、内積と外積が得られます。
\vec{v}\vec{w}=-\underbrace{\vec{v}\cdot\vec{w}}_{内積}+\underbrace{\vec{v}×\vec{w}}_{外積}
計算過程は八元数の積をプログラムで確認を参照してください。
外積(ベクトル積)が3次元と7次元でしか定義できないのは、四元数と八元数に関係があります。
詳細は以下の記事を参照してください。($ℓ$ を前置する流儀です)
共役
共役は四元数と同様に虚部の符号反転です。
\begin{align}
&(a_1+a_2i+a_3j+a_4k+a_5h+a_6i_h+a_7j_h+a_8k_h)^* \\
&=a_1-a_2i-a_3j-a_4k-a_5h-a_6i_h-a_7j_h-a_8k_h
\end{align}
ノルム
ノルムの2乗を計算すればユークリッド型になることが確認できます。
\begin{align}
&\|a_1+a_2i+a_3j+a_4k+a_5h+a_6i_h+a_7j_h+a_8k_h\|^2 \\
&=a_1^2+a_2^2+a_3^2+a_4^2+a_5^2+a_6^2+a_7^2+a_8^2
\end{align}
計算過程は八元数の積をプログラムで確認を参照してください。
プログラム
反結合性と例外をパターンに分類して八元数の乗積表を作るプログラムです。(*) に注目してください。(リポジトリ)
type Octonion =
E | I | J | K | H of Octonion
override x.ToString() =
match x with
| E -> "1" | I -> "i" | J -> "j" | K -> "k"
| H E -> "h"
| H x -> string x + "h"
member x.Next =
match x with
| I -> J
| J -> K
| K -> I
| H x -> H x.Next
| x -> x
static member (*)(a:Octonion, b:Octonion) =
match a, b with
| x, E -> 1, x // i1 = i
| E, y -> 1, y // 1i = i
| x, y when x = y -> -1, E // ii = -1
| H x, H E -> -1, x // (ih)h = -i
| H x, H y -> y * x // (ih)(jh) = ji
| x, H E -> 1, H x // ih = (ih)
| x, H y when x = y -> -1, H E // i(ih) = -h
| x, H y -> let c, z = y * x // i(jh) = (ji)h
c, H z
| x, y when x.Next = y // ij = k
-> 1, y.Next
| x, y -> let c, z = y * x // ji = -ij
-c, z
let str (a, z) =
(if a = -1 then "-" else " ") + string z
|> sprintf "%-3s"
let elems = [E; I; J; K; H E; H I; H J; H K]
for x in elems do
elems
|> List.map ((*) x >> str)
|> String.concat " "
|> printfn "%s"
1 i j k h ih jh kh
i -1 k -j ih -h -kh jh
j -k -1 i jh kh -h -ih
k j -i -1 kh -jh ih -h
h -ih -jh -kh -1 i j k
ih h -kh jh -i -1 -k j
jh kh h -ih -j k -1 -i
kh -jh ih h -k -j i -1
参考
多元数
多元数のバリエーションをまとめました。
| 基本 | 双 | 分解型 | 分解型双 | 双曲 | 双対 |
|---|---|---|---|---|---|
| 複素数 | 双複素数 | 分解型複素数 | |||
| 四元数 | 双四元数 | 分解型四元数 | 分解型双四元数 | 双曲四元数 | 双対四元数 |
| 八元数 | 双八元数 | 分解型八元数 | |||
| 十六元数 |