十六元数を作ろう

四元数・八元数に引き続き十六元数を作ります。四元数・八元数を復習しながら進めます。十六元数の元の積の計算過程をプログラムで生成します。

十六元数を使う機会はあまりないかもしれませんが、演算規則を理解するのに高度な前提知識は不要ですし、一度やっておけば視野が広がるのでお勧めです。八元数がコンパクトに感じて来ます。

※ 元の積の計算方法に焦点を絞って、乗積表を見ずに導出するための事項を説明します。数学的な性質は零因子に簡単に触れるだけに留めます。

シリーズの記事です。

1. 多項式の積を計算
2. 外積と愉快な仲間たち
3. ユークリッド空間のホッジ双対とバブルソート
4. 四元数を作ろう
5. 四元数と行列で見る内積と外積の「内」と「外」
6. 八元数を作ろう
7. 八元数の積をプログラムで確認
8. 外積の成分をプログラムで確認
9. 多元数の積の構成
10. 十六元数を作ろう ← この記事

関連するコードをまとめたリポジトリです。

• https://bitbucket.org/7shi/math7

この記事には関連記事があります。

• 2017.12.04 八元数と7次元の外積 ← お勧め

ケーリー=ディクソンの構成法

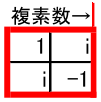
複素数は実数と1つの虚数単位 $i$ で構成されます。

a_0+a_1i

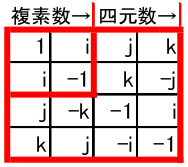
四元数は複素数を係数にして別の虚数単位 $j$ でネストさせます。$ij=k$ とします。

(a_0+a_1i)+(a_2+a_3i)j=a_0+a_1i+a_2j+a_3k

このようにネストで多元数を作り出す方法をケーリー=ディクソンの構成法と呼びます。

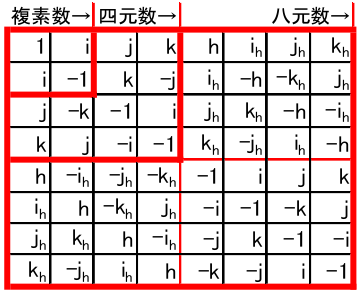
八元数は四元数を係数にして別の虚数単位 $h$ でネストさせます。$h$ と複合した元は1つの元と見なします。

\begin{align}
&(a_0+a_1i+a_2j+a_3k)+(a_4+a_5i+a_6j+a_7k)h \\
&=a_0+a_1i+a_2j+a_3k+a_4h+a_5i_h+a_6j_h+a_7k_h
\end{align}

※ $h$ が結合した元は $ih=i_h$ のように添え字で書きます。これは一般的な流儀ではありませんが、元を構成する因子が分かりやすいため採用しました。

十六元数は八元数を係数にして別の虚数単位 $ℓ$ でネストさせます。$ℓ$ と複合した元は1つの元と見なします。

\begin{align}
&(a_0+a_1i+a_2j+a_3k+a_4h+a_5i_h+a_6j_h+a_7k_h) \\
&\quad +(a_8+a_9i+a_{10}j+a_{11}k+a_{12}h+a_{13}i_h+a_{14}j_h+a_{15}k_h)ℓ \\
&=a_0+a_1i+a_2j+a_3k+a_4h+a_5i_h+a_6j_h+a_7k_h \\
&\quad +a_8ℓ+a_9i_ℓ+a_{10}j_ℓ+a_{11}k_ℓ+a_{12}h_ℓ+a_{13}i_{hℓ}+a_{14}j_{hℓ}+a_{15}k_{hℓ}
\end{align}

※ $ℓ$ が結合した元は $iℓ=i_ℓ$ のように添え字で書きます。$h$ を含む元との複合では $i_{hℓ}$ のように $ℓ$ を後ろに書きます。これは一般的な流儀ではありませんが、元を構成する因子が分かりやすいため採用しました。

多元数は複素数から出発して、ケーリー=ディクソン構成を適用するごとに拡張されます。複素数→四元数→八元数→十六元数は上位互換での拡張となっており、下位の乗積表をそのまま含みます。

計算ルール

虚数単位（元）の積の計算ルールを示します。ルールには優先度があり、1から順番に合致するか確認します。例えば $ii_h$ は3にも4にも合致しますが、必ず3を適用します。どれを使っても同じ結果になるわけではないため、もし4を適用すれば間違った計算結果となります。

※ 以下に出て来る用語の「反」は符号の反転を意味します。

1. 元の2乗は$-1$。
   $i^2=j^2=k^2=h^2=i_h^2=j_h^2=k_h^2=ℓ^2=i_ℓ^2=j_ℓ^2=k_ℓ^2=h_ℓ^2=i_{hℓ}^2=j_{hℓ}^2=k_{hℓ}^2=-1$
2. 反交換性（積の順序を入れ替えると符号が反転する）
   【例】 $ij=-ji,\ i_hj_{hℓ}=-j_{hℓ}i_h$
3. 交代結合性（同じ元が括弧1つを挟んで隣接していれば、括弧を飛び越えて優先的に結合する）
   【例】 $ii_h=i(ih)=(ii)h=-h,\ i_hh=(ih)h=i(hh)=-i$
4. 反結合性（$h,ℓ$ を含む元の結合を変更するとき符号が反転する、ただし $h_ℓ$ を除く）
   【例】 $ij_h=i(jh)=-(ij)h=-kh,\ i(jh_ℓ)=(ij)h_ℓ$

1は複素数、2は四元数、3と4は八元数から受け継いでいます。八元数から増えたルールは4の $h_ℓ$ に関する例外くらいで、八元数を知っていればすぐ計算できます。

※ 文献によっては反交換性を交代性と呼んだり、交代結合性を交代性と呼んだりするようです。この記事では当初、交代結合性のことを交代性と書いていましたが、混乱を避けるため交代結合性に書き換えました。

• 参考: 分配多元環 - Wikipedia

計算ルールを複素数から順番に追って行きます。

複素数

元 $i$ を2乗すると $-1$ になります。

i^2=-1

四元数

元 $j$ を追加します。積により生じる複合的な元 $ij$ は $k$ と表記して独立した元として扱います。

ij=k

新しく追加された元も2乗すると $-1$ になります。

j^2=k^2=-1

2つの異なる元の積からは、どちらとも異なる元が生じます。巡回方向（$i→j→k→i→j→\cdots$）を正とします。

ij=k,\ jk=i,\ ki=j \\
ji=-k,\ kj=-i,\ ik=-j

この関係より反交換性（積の順序を入れ替えると符号が反転する）が認められます。

ij=-ji=k,\ jk=-kj=i,\ ki=-ik=j

八元数

元 $h$ を追加します。積により生じる複合的な元は $h$ を後ろから掛けたものを正として、独立した元として扱います。

ih=i_h,\ jh=j_h,\ kh=k_h

この関係にも反交換性が適用されます。

ih=-hi=i_h,\ jh=-hj=j_h,\ kh=-hk=k_h

新しく追加された元も2乗すると $-1$ になります。

h^2=i_h^2=j_h^2=k_h^2=-1

2つの異なる元の積からは、どちらとも異なる元が生じます。$h$ と複合した元は括弧書きで因子に分解してから計算します。後で述べますが $h$ は結合法則を満たさないため、括弧書きを省略してはいけません。

ii_h=i(ih) \\
i_hh=(ih)h \\
ij_h=i(jh) \\
i_hj_h=(ih)(jh)

括弧を挟んで同じ元が並んでいれば、優先的に結合して $-1$ となります（交代結合性）。

ii_h=\underbrace{i(i}_{-1}h)=-h \\
i_hh=(i\underbrace{h)h}_{-1}=-i

同じ元があっても隣接していない場合は、先に反交換性を適用して隣接させてから結合させます。

\underbrace{i_hi}_{交換}=-ii_h=-\underbrace{i(i}_{-1}h)=h

$h$ は結合法則を満たしません。$h$ との結合を分解する際に符号が反転します（反結合性）。これが括弧書きを省略できない理由です。

ij_h=i\underbrace{(jh)}_{分解}=-\underbrace{(ij)}_{k}h=-kh \\
i_hj_h=(ih)\underbrace{(jh)}_{分解}=-(\underbrace{(ih)j}_{交換})h=(j\underbrace{(ih)}_{分解})h=-((ji)\underbrace{h)h}_{-1}=ji=-k

交代結合性と反結合性を使えば、すべての元の組み合わせを計算できます。

よくある間違い

計算ルールの優先順位を守らないと正しい計算結果が得られません。いくつか例を示します。

※ 慣れないと違和感があるかもしれません。私見ですが、計算ルールが先にあって八元数の性質が決まるのではなく、八元数の性質が先にあって計算ルールが決められているように感じます。

元の2乗

同じ元同士の結合を後回しにして分解してはいけません。

\begin{align}
【正】\ &\underbrace{i_hi_h}_{結合}=(i_h)^2=-1 \\
【誤】\ &i_hi_h=(ih)\underbrace{(ih)}_{分解}=\underbrace{-((ih)i)h}_{間違い}=(i(ih))h=(-h)h=1
\end{align}

交代結合性

同じ元が複数ある場合、反交換性で隣接させて先に結合させます。結合を後回しにして分解してはいけません。

\begin{align}
【正】\ &\underbrace{hi_h}_{交換}=-i_hh=-(i\underbrace{h)h}_{-1}=i \\
【誤】\ &hi_h=h\underbrace{(ih)}_{分解}=\underbrace{-(hi)h}_{間違い}=(ih)h=-i
\end{align}

十六元数

元 $ℓ$ を追加します。$h$ と $ℓ$ は同じ性質を持ちますが、両方が含まれる元は取り扱いに注意が必要です。

積により生じる複合的な元は $ℓ$ を後ろから掛けたものを正として、独立した元として扱います。$h$ と複合する場合も $ℓ$ が後ろに来るように正規化します。

iℓ=i_ℓ,\ hℓ=h_ℓ,\ i_hℓ=i_{hℓ}

※ $i_{hℓ}$ は $ℓ$ が後から掛かっているため $(ih)ℓ$ です。$i(hℓ)$ ではありません。

この関係にも反交換性が適用されます。

iℓ=-ℓi=i_ℓ,\ hℓ=-ℓh=h_ℓ,\ i_hℓ=-ℓi_h=i_{hℓ}

$ℓ$ は $h$ と同様に交代結合性と反結合性を持ちます。

ih_ℓ=i\underbrace{(hℓ)}_{分解}=-(ih)ℓ \\
ij_{hℓ}=i\underbrace{((jh)ℓ)}_{分解}=-(i\underbrace{(jh)}_{分解})ℓ=(\underbrace{(ij)}_{k}h)ℓ=(kh)ℓ=k_{hℓ}

例外

$h_ℓ$ を分解しないでその結合相手を変更する際には、符号は反転しません。

i(jh_ℓ)=(ij)h_ℓ

これは結果としてそうなるということで、なるべくこのような変形は避けた方が無難です。原則としてはまず先に $h_ℓ$ を分解して、$h$ を別の元と結合させてから計算してください。

i(jh_ℓ)=i(j\underbrace{(hℓ)}_{分解})=-i\underbrace{((jh)ℓ)}_{分解}=(i\underbrace{(jh)}_{分解})ℓ=-\underbrace{((ij)h)}_{分解}ℓ=(ij)(hℓ)

零因子

十六元数の計算ルールは八元数と大差ありませんが、十六元数では零因子が発生します。0ではないものを掛けて0になることがあるという意味です。

\begin{align}
【例】\ 
&(k+j_ℓ)(j_h-k_{hℓ}) \\
&=kj_h-kk_{hℓ}+j_ℓj_h-j_ℓk_{hℓ} \\
&=k\underbrace{(jh)}_{分解}-k(\underbrace{(kh)}_{分解}ℓ)+\underbrace{(jℓ)}_{交換}\underbrace{(jh)}_{分解}-\underbrace{(jℓ)}_{分解}(\underbrace{(kh)ℓ)}_{交換} \\
&=-\underbrace{(kj)}_{-i}h+\underbrace{k(k}_{-1}(hℓ))+((ℓ\underbrace{j)j}_{-1})h-j(\underbrace{ℓ(ℓ}_{-1}(kh))) \\
&=ih-hℓ-\underbrace{ℓh}_{交換}+j\underbrace{(kh)}_{分解} \\
&=ih-hℓ+hℓ-\underbrace{(jk)}_{i}h \\
&=i_h-h_ℓ+h_ℓ-i_h \\
&=0
\end{align}

• 出典: 十六元数 - Wikipedia

八元数には零因子はないため、十六元数は八元数よりも演算上の制約が多くなっています。

零因子は行列を思い浮かべる分かりやすいかもしれません。$AB=O$ であっても $A$ や $B$ が零行列であるとは限りません。

【例】\ 
\left(\begin{matrix}0 & 1 \\ 0 & 2\end{matrix}\right)
\left(\begin{matrix}3 & 4 \\ 0 & 0\end{matrix}\right)
=\left(\begin{matrix}0 & 0 \\ 0 & 0\end{matrix}\right)

• 出典: 零因子，可換性

行列の積は結合法則を満たしますが、八元数や十六元数ではその限りではありません。そのため八元数や十六元数は行列で表現できません。

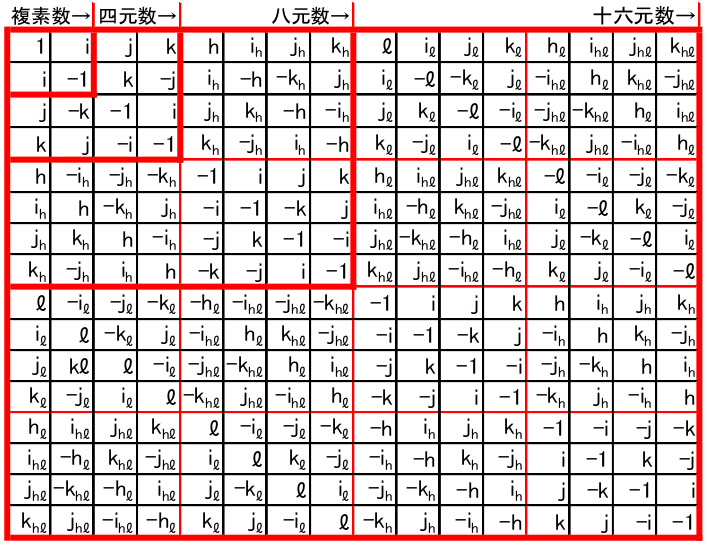
計算過程

元の積は $16×16=256$ 通りあります。$4×4$ ごとの領域に分割して、計算パターンを示します。$1$ との積は自明なため省略します。

\begin{align}
i^2&=-1 \\
ij&=k \\
ik&=-ki=-j \\
ji&=-ij=-k \\
j^2&=-1 \\
jk&=i \\
ki&=j \\
kj&=-jk=-i \\
k^2&=-1 \\
\hline
ih&=i_h \\
ii_h&=i(ih)=-h \\
ij_h&=i(jh)=-(ij)h=-kh=-k_h \\
ik_h&=i(kh)=-(ik)h=jh=j_h \\
jh&=j_h \\
ji_h&=j(ih)=-(ji)h=kh=k_h \\
jj_h&=j(jh)=-h \\
jk_h&=j(kh)=-(jk)h=-ih=-i_h \\
kh&=k_h \\
ki_h&=k(ih)=-(ki)h=-jh=-j_h \\
kj_h&=k(jh)=-(kj)h=ih=i_h \\
kk_h&=k(kh)=-h \\
\hline
i{\ell}&=i_{\ell} \\
ii_{\ell}&=i(i\ell)=-\ell \\
ij_{\ell}&=i(j\ell)=-(ij)\ell=-k\ell=-k_{\ell} \\
ik_{\ell}&=i(k\ell)=-(ik)\ell=j\ell=j_{\ell} \\
j{\ell}&=j_{\ell} \\
ji_{\ell}&=j(i\ell)=-(ji)\ell=k\ell=k_{\ell} \\
jj_{\ell}&=j(j\ell)=-\ell \\
jk_{\ell}&=j(k\ell)=-(jk)\ell=-i\ell=-i_{\ell} \\
k{\ell}&=k_{\ell} \\
ki_{\ell}&=k(i\ell)=-(ki)\ell=-j\ell=-j_{\ell} \\
kj_{\ell}&=k(j\ell)=-(kj)\ell=i\ell=i_{\ell} \\
kk_{\ell}&=k(k\ell)=-\ell \\
\hline
ih_{\ell}&=i(h\ell)=-(ih)\ell=-i_{h\ell} \\
ii_{h\ell}&=i(i_h\ell)=-(ii_h)\ell=h\ell=h_{\ell} \\
ij_{h\ell}&=i(j_h\ell)=-(ij_h)\ell=k_h\ell=k_{h\ell} \\
ik_{h\ell}&=i(k_h\ell)=-(ik_h)\ell=-j_h\ell=-j_{h\ell} \\
jh_{\ell}&=j(h\ell)=-(jh)\ell=-j_{h\ell} \\
ji_{h\ell}&=j(i_h\ell)=-(ji_h)\ell=-k_h\ell=-k_{h\ell} \\
jj_{h\ell}&=j(j_h\ell)=-(jj_h)\ell=h\ell=h_{\ell} \\
jk_{h\ell}&=j(k_h\ell)=-(jk_h)\ell=i_h\ell=i_{h\ell} \\
kh_{\ell}&=k(h\ell)=-(kh)\ell=-k_{h\ell} \\
ki_{h\ell}&=k(i_h\ell)=-(ki_h)\ell=j_h\ell=j_{h\ell} \\
kj_{h\ell}&=k(j_h\ell)=-(kj_h)\ell=-i_h\ell=-i_{h\ell} \\
kk_{h\ell}&=k(k_h\ell)=-(kk_h)\ell=h\ell=h_{\ell} \\
\hline
hi&=-ih=-i_h \\
hj&=-jh=-j_h \\
hk&=-kh=-k_h \\
i_hi&=-ii_h=-i(ih)=h \\
i_hj&=-ji_h=-j(ih)=(ji)h=-kh=-k_h \\
i_hk&=-ki_h=-k(ih)=(ki)h=jh=j_h \\
j_hi&=-ij_h=-i(jh)=(ij)h=kh=k_h \\
j_hj&=-jj_h=-j(jh)=h \\
j_hk&=-kj_h=-k(jh)=(kj)h=-ih=-i_h \\
k_hi&=-ik_h=-i(kh)=(ik)h=-jh=-j_h \\
k_hj&=-jk_h=-j(kh)=(jk)h=ih=i_h \\
k_hk&=-kk_h=-k(kh)=h \\
\hline
h^2&=-1 \\
hi_h&=-i_hh=-(ih)h=i \\
hj_h&=-j_hh=-(jh)h=j \\
hk_h&=-k_hh=-(kh)h=k \\
i_hh&=(ih)h=-i \\
i_h^2&=-1 \\
i_hj_h&=(ih)(jh)=-(ih)(hj)=((ih)h)j=-ij=-k \\
i_hk_h&=(ih)(kh)=-(ih)(hk)=((ih)h)k=-ik=j \\
j_hh&=(jh)h=-j \\
j_hi_h&=(jh)(ih)=-(jh)(hi)=((jh)h)i=-ji=k \\
j_h^2&=-1 \\
j_hk_h&=(jh)(kh)=-(jh)(hk)=((jh)h)k=-jk=-i \\
k_hh&=(kh)h=-k \\
k_hi_h&=(kh)(ih)=-(kh)(hi)=((kh)h)i=-ki=-j \\
k_hj_h&=(kh)(jh)=-(kh)(hj)=((kh)h)j=-kj=i \\
k_h^2&=-1 \\
\hline
h{\ell}&=h_{\ell} \\
hi_{\ell}&=h(i\ell)=-(hi)\ell=(ih)\ell=i_{h\ell} \\
hj_{\ell}&=h(j\ell)=-(hj)\ell=(jh)\ell=j_{h\ell} \\
hk_{\ell}&=h(k\ell)=-(hk)\ell=(kh)\ell=k_{h\ell} \\
i_h{\ell}&=i_{h\ell} \\
i_hi_{\ell}&=i_h(i\ell)=-(i_hi)\ell=(ii_h)\ell=-h_{\ell} \\
i_hj_{\ell}&=i_h(j\ell)=-(i_hj)\ell=(kh)\ell=k_{h\ell} \\
i_hk_{\ell}&=i_h(k\ell)=-(i_hk)\ell=-(jh)\ell=-j_{h\ell} \\
j_h{\ell}&=j_{h\ell} \\
j_hi_{\ell}&=j_h(i\ell)=-(j_hi)\ell=-(kh)\ell=-k_{h\ell} \\
j_hj_{\ell}&=j_h(j\ell)=-(j_hj)\ell=(jj_h)\ell=-h_{\ell} \\
j_hk_{\ell}&=j_h(k\ell)=-(j_hk)\ell=(ih)\ell=i_{h\ell} \\
k_h{\ell}&=k_{h\ell} \\
k_hi_{\ell}&=k_h(i\ell)=-(k_hi)\ell=(jh)\ell=j_{h\ell} \\
k_hj_{\ell}&=k_h(j\ell)=-(k_hj)\ell=-(ih)\ell=-i_{h\ell} \\
k_hk_{\ell}&=k_h(k\ell)=-(k_hk)\ell=(kk_h)\ell=-h_{\ell} \\
\hline
hh_{\ell}&=h(h\ell)=-\ell \\
hi_{h\ell}&=h((ih)\ell)=-(h(ih))\ell=((ih)h)\ell=-i\ell=-i_{\ell} \\
hj_{h\ell}&=h((jh)\ell)=-(h(jh))\ell=((jh)h)\ell=-j\ell=-j_{\ell} \\
hk_{h\ell}&=h((kh)\ell)=-(h(kh))\ell=((kh)h)\ell=-k\ell=-k_{\ell} \\
i_hh_{\ell}&=(ih)(h\ell)=-((ih)h)\ell=i\ell=i_{\ell} \\
i_hi_{h\ell}&=i_h(i_h\ell)=-\ell \\
i_hj_{h\ell}&=i_h(j_h\ell)=-(i_hj_h)\ell=(k)\ell=k_{\ell} \\
i_hk_{h\ell}&=i_h(k_h\ell)=-(i_hk_h)\ell=-(j)\ell=-j_{\ell} \\
j_hh_{\ell}&=(jh)(h\ell)=-((jh)h)\ell=j\ell=j_{\ell} \\
j_hi_{h\ell}&=j_h(i_h\ell)=-(j_hi_h)\ell=-(k)\ell=-k_{\ell} \\
j_hj_{h\ell}&=j_h(j_h\ell)=-\ell \\
j_hk_{h\ell}&=j_h(k_h\ell)=-(j_hk_h)\ell=(i)\ell=i_{\ell} \\
k_hh_{\ell}&=(kh)(h\ell)=-((kh)h)\ell=k\ell=k_{\ell} \\
k_hi_{h\ell}&=k_h(i_h\ell)=-(k_hi_h)\ell=(j)\ell=j_{\ell} \\
k_hj_{h\ell}&=k_h(j_h\ell)=-(k_hj_h)\ell=-(i)\ell=-i_{\ell} \\
k_hk_{h\ell}&=k_h(k_h\ell)=-\ell \\
\hline
{\ell}i&=-i{\ell}=-i_{\ell} \\
{\ell}j&=-j{\ell}=-j_{\ell} \\
{\ell}k&=-k{\ell}=-k_{\ell} \\
i_{\ell}i&=-ii_{\ell}=-i(i\ell)=\ell \\
i_{\ell}j&=-ji_{\ell}=-j(i\ell)=(ji)\ell=-k\ell=-k_{\ell} \\
i_{\ell}k&=-ki_{\ell}=-k(i\ell)=(ki)\ell=j\ell=j_{\ell} \\
j_{\ell}i&=-ij_{\ell}=-i(j\ell)=(ij)\ell=k\ell=k_{\ell} \\
j_{\ell}j&=-jj_{\ell}=-j(j\ell)=\ell \\
j_{\ell}k&=-kj_{\ell}=-k(j\ell)=(kj)\ell=-i\ell=-i_{\ell} \\
k_{\ell}i&=-ik_{\ell}=-i(k\ell)=(ik)\ell=-j\ell=-j_{\ell} \\
k_{\ell}j&=-jk_{\ell}=-j(k\ell)=(jk)\ell=i\ell=i_{\ell} \\
k_{\ell}k&=-kk_{\ell}=-k(k\ell)=\ell \\
\hline
{\ell}h&=-h{\ell}=-h_{\ell} \\
{\ell}i_h&=-i_h{\ell}=-i_{h\ell} \\
{\ell}j_h&=-j_h{\ell}=-j_{h\ell} \\
{\ell}k_h&=-k_h{\ell}=-k_{h\ell} \\
i_{\ell}h&=-hi_{\ell}=-h(i\ell)=(hi)\ell=-(ih)\ell=-i_{h\ell} \\
i_{\ell}i_h&=-i_hi_{\ell}=-i_h(i\ell)=(i_hi)\ell=-(ii_h)\ell=h_{\ell} \\
i_{\ell}j_h&=-j_hi_{\ell}=-j_h(i\ell)=(j_hi)\ell=(kh)\ell=k_{h\ell} \\
i_{\ell}k_h&=-k_hi_{\ell}=-k_h(i\ell)=(k_hi)\ell=-(jh)\ell=-j_{h\ell} \\
j_{\ell}h&=-hj_{\ell}=-h(j\ell)=(hj)\ell=-(jh)\ell=-j_{h\ell} \\
j_{\ell}i_h&=-i_hj_{\ell}=-i_h(j\ell)=(i_hj)\ell=-(kh)\ell=-k_{h\ell} \\
j_{\ell}j_h&=-j_hj_{\ell}=-j_h(j\ell)=(j_hj)\ell=-(jj_h)\ell=h_{\ell} \\
j_{\ell}k_h&=-k_hj_{\ell}=-k_h(j\ell)=(k_hj)\ell=(ih)\ell=i_{h\ell} \\
k_{\ell}h&=-hk_{\ell}=-h(k\ell)=(hk)\ell=-(kh)\ell=-k_{h\ell} \\
k_{\ell}i_h&=-i_hk_{\ell}=-i_h(k\ell)=(i_hk)\ell=(jh)\ell=j_{h\ell} \\
k_{\ell}j_h&=-j_hk_{\ell}=-j_h(k\ell)=(j_hk)\ell=-(ih)\ell=-i_{h\ell} \\
k_{\ell}k_h&=-k_hk_{\ell}=-k_h(k\ell)=(k_hk)\ell=-(kk_h)\ell=h_{\ell} \\
\hline
{\ell}^2&=-1 \\
{\ell}i_{\ell}&=-i_{\ell}{\ell}=-(i\ell)\ell=i \\
{\ell}j_{\ell}&=-j_{\ell}{\ell}=-(j\ell)\ell=j \\
{\ell}k_{\ell}&=-k_{\ell}{\ell}=-(k\ell)\ell=k \\
i_{\ell}{\ell}&=(i\ell)\ell=-i \\
i_{\ell}^2&=-1 \\
i_{\ell}j_{\ell}&=(i\ell)(j\ell)=-(i\ell)({\ell}j)=((i\ell)\ell)j=-ij=-k \\
i_{\ell}k_{\ell}&=(i\ell)(k\ell)=-(i\ell)({\ell}k)=((i\ell)\ell)k=-ik=j \\
j_{\ell}{\ell}&=(j\ell)\ell=-j \\
j_{\ell}i_{\ell}&=(j\ell)(i\ell)=-(j\ell)({\ell}i)=((j\ell)\ell)i=-ji=k \\
j_{\ell}^2&=-1 \\
j_{\ell}k_{\ell}&=(j\ell)(k\ell)=-(j\ell)({\ell}k)=((j\ell)\ell)k=-jk=-i \\
k_{\ell}{\ell}&=(k\ell)\ell=-k \\
k_{\ell}i_{\ell}&=(k\ell)(i\ell)=-(k\ell)({\ell}i)=((k\ell)\ell)i=-ki=-j \\
k_{\ell}j_{\ell}&=(k\ell)(j\ell)=-(k\ell)({\ell}j)=((k\ell)\ell)j=-kj=i \\
k_{\ell}^2&=-1 \\
\hline
{\ell}h_{\ell}&=-h_{\ell}{\ell}=-(h\ell)\ell=h \\
{\ell}i_{h\ell}&=-i_{h\ell}{\ell}=-(i_h\ell)\ell=i_h \\
{\ell}j_{h\ell}&=-j_{h\ell}{\ell}=-(j_h\ell)\ell=j_h \\
{\ell}k_{h\ell}&=-k_{h\ell}{\ell}=-(k_h\ell)\ell=k_h \\
i_{\ell}h_{\ell}&=(i\ell)(h\ell)=-(i\ell)({\ell}h)=((i\ell)\ell)h=-ih=-i_h \\
i_{\ell}i_{h\ell}&=(i\ell)(i_h\ell)=-(i\ell)({\ell}i_h)=((i\ell)\ell)i_h=-ii_h=h \\
i_{\ell}j_{h\ell}&=(i\ell)(j_h\ell)=-(i\ell)({\ell}j_h)=((i\ell)\ell)j_h=-ij_h=k_h \\
i_{\ell}k_{h\ell}&=(i\ell)(k_h\ell)=-(i\ell)({\ell}k_h)=((i\ell)\ell)k_h=-ik_h=-j_h \\
j_{\ell}h_{\ell}&=(j\ell)(h\ell)=-(j\ell)({\ell}h)=((j\ell)\ell)h=-jh=-j_h \\
j_{\ell}i_{h\ell}&=(j\ell)(i_h\ell)=-(j\ell)({\ell}i_h)=((j\ell)\ell)i_h=-ji_h=-k_h \\
j_{\ell}j_{h\ell}&=(j\ell)(j_h\ell)=-(j\ell)({\ell}j_h)=((j\ell)\ell)j_h=-jj_h=h \\
j_{\ell}k_{h\ell}&=(j\ell)(k_h\ell)=-(j\ell)({\ell}k_h)=((j\ell)\ell)k_h=-jk_h=i_h \\
k_{\ell}h_{\ell}&=(k\ell)(h\ell)=-(k\ell)({\ell}h)=((k\ell)\ell)h=-kh=-k_h \\
k_{\ell}i_{h\ell}&=(k\ell)(i_h\ell)=-(k\ell)({\ell}i_h)=((k\ell)\ell)i_h=-ki_h=j_h \\
k_{\ell}j_{h\ell}&=(k\ell)(j_h\ell)=-(k\ell)({\ell}j_h)=((k\ell)\ell)j_h=-kj_h=-i_h \\
k_{\ell}k_{h\ell}&=(k\ell)(k_h\ell)=-(k\ell)({\ell}k_h)=((k\ell)\ell)k_h=-kk_h=h \\
\hline
h_{\ell}i&=-ih_{\ell}=-i(h\ell)=(ih)\ell=i_{h\ell} \\
h_{\ell}j&=-jh_{\ell}=-j(h\ell)=(jh)\ell=j_{h\ell} \\
h_{\ell}k&=-kh_{\ell}=-k(h\ell)=(kh)\ell=k_{h\ell} \\
i_{h\ell}i&=-ii_{h\ell}=-i(i_h\ell)=(ii_h)\ell=-h\ell=-h_{\ell} \\
i_{h\ell}j&=-ji_{h\ell}=-j(i_h\ell)=(ji_h)\ell=k_h\ell=k_{h\ell} \\
i_{h\ell}k&=-ki_{h\ell}=-k(i_h\ell)=(ki_h)\ell=-j_h\ell=-j_{h\ell} \\
j_{h\ell}i&=-ij_{h\ell}=-i(j_h\ell)=(ij_h)\ell=-k_h\ell=-k_{h\ell} \\
j_{h\ell}j&=-jj_{h\ell}=-j(j_h\ell)=(jj_h)\ell=-h\ell=-h_{\ell} \\
j_{h\ell}k&=-kj_{h\ell}=-k(j_h\ell)=(kj_h)\ell=i_h\ell=i_{h\ell} \\
k_{h\ell}i&=-ik_{h\ell}=-i(k_h\ell)=(ik_h)\ell=j_h\ell=j_{h\ell} \\
k_{h\ell}j&=-jk_{h\ell}=-j(k_h\ell)=(jk_h)\ell=-i_h\ell=-i_{h\ell} \\
k_{h\ell}k&=-kk_{h\ell}=-k(k_h\ell)=(kk_h)\ell=-h\ell=-h_{\ell} \\
\hline
h_{\ell}h&=-hh_{\ell}=-h(h\ell)=\ell \\
h_{\ell}i_h&=-i_hh_{\ell}=-(ih)(h\ell)=((ih)h)\ell=-i\ell=-i_{\ell} \\
h_{\ell}j_h&=-j_hh_{\ell}=-(jh)(h\ell)=((jh)h)\ell=-j\ell=-j_{\ell} \\
h_{\ell}k_h&=-k_hh_{\ell}=-(kh)(h\ell)=((kh)h)\ell=-k\ell=-k_{\ell} \\
i_{h\ell}h&=-hi_{h\ell}=-h((ih)\ell)=(h(ih))\ell=-((ih)h)\ell=i\ell=i_{\ell} \\
i_{h\ell}i_h&=-i_hi_{h\ell}=-i_h(i_h\ell)=\ell \\
i_{h\ell}j_h&=-j_hi_{h\ell}=-j_h(i_h\ell)=(j_hi_h)\ell=(k)\ell=k_{\ell} \\
i_{h\ell}k_h&=-k_hi_{h\ell}=-k_h(i_h\ell)=(k_hi_h)\ell=-(j)\ell=-j_{\ell} \\
j_{h\ell}h&=-hj_{h\ell}=-h((jh)\ell)=(h(jh))\ell=-((jh)h)\ell=j\ell=j_{\ell} \\
j_{h\ell}i_h&=-i_hj_{h\ell}=-i_h(j_h\ell)=(i_hj_h)\ell=-(k)\ell=-k_{\ell} \\
j_{h\ell}j_h&=-j_hj_{h\ell}=-j_h(j_h\ell)=\ell \\
j_{h\ell}k_h&=-k_hj_{h\ell}=-k_h(j_h\ell)=(k_hj_h)\ell=(i)\ell=i_{\ell} \\
k_{h\ell}h&=-hk_{h\ell}=-h((kh)\ell)=(h(kh))\ell=-((kh)h)\ell=k\ell=k_{\ell} \\
k_{h\ell}i_h&=-i_hk_{h\ell}=-i_h(k_h\ell)=(i_hk_h)\ell=(j)\ell=j_{\ell} \\
k_{h\ell}j_h&=-j_hk_{h\ell}=-j_h(k_h\ell)=(j_hk_h)\ell=-(i)\ell=-i_{\ell} \\
k_{h\ell}k_h&=-k_hk_{h\ell}=-k_h(k_h\ell)=\ell \\
\hline
h_{\ell}{\ell}&=(h\ell)\ell=-h \\
h_{\ell}i_{\ell}&=(h\ell)(i\ell)=-(h\ell)({\ell}i)=((h\ell)\ell)i=-hi=i_h \\
h_{\ell}j_{\ell}&=(h\ell)(j\ell)=-(h\ell)({\ell}j)=((h\ell)\ell)j=-hj=j_h \\
h_{\ell}k_{\ell}&=(h\ell)(k\ell)=-(h\ell)({\ell}k)=((h\ell)\ell)k=-hk=k_h \\
i_{h\ell}{\ell}&=(i_h\ell)\ell=-i_h \\
i_{h\ell}i_{\ell}&=(i_h\ell)(i\ell)=-(i_h\ell)({\ell}i)=((i_h\ell)\ell)i=-i_hi=-h \\
i_{h\ell}j_{\ell}&=(i_h\ell)(j\ell)=-(i_h\ell)({\ell}j)=((i_h\ell)\ell)j=-i_hj=k_h \\
i_{h\ell}k_{\ell}&=(i_h\ell)(k\ell)=-(i_h\ell)({\ell}k)=((i_h\ell)\ell)k=-i_hk=-j_h \\
j_{h\ell}{\ell}&=(j_h\ell)\ell=-j_h \\
j_{h\ell}i_{\ell}&=(j_h\ell)(i\ell)=-(j_h\ell)({\ell}i)=((j_h\ell)\ell)i=-j_hi=-k_h \\
j_{h\ell}j_{\ell}&=(j_h\ell)(j\ell)=-(j_h\ell)({\ell}j)=((j_h\ell)\ell)j=-j_hj=-h \\
j_{h\ell}k_{\ell}&=(j_h\ell)(k\ell)=-(j_h\ell)({\ell}k)=((j_h\ell)\ell)k=-j_hk=i_h \\
k_{h\ell}{\ell}&=(k_h\ell)\ell=-k_h \\
k_{h\ell}i_{\ell}&=(k_h\ell)(i\ell)=-(k_h\ell)({\ell}i)=((k_h\ell)\ell)i=-k_hi=j_h \\
k_{h\ell}j_{\ell}&=(k_h\ell)(j\ell)=-(k_h\ell)({\ell}j)=((k_h\ell)\ell)j=-k_hj=-i_h \\
k_{h\ell}k_{\ell}&=(k_h\ell)(k\ell)=-(k_h\ell)({\ell}k)=((k_h\ell)\ell)k=-k_hk=-h \\
\hline
h_{\ell}^2&=-1 \\
h_{\ell}i_{h\ell}&=(h\ell)(i_h\ell)=-(h\ell)({\ell}i_h)=((h\ell)\ell)i_h=-hi_h=-i \\
h_{\ell}j_{h\ell}&=(h\ell)(j_h\ell)=-(h\ell)({\ell}j_h)=((h\ell)\ell)j_h=-hj_h=-j \\
h_{\ell}k_{h\ell}&=(h\ell)(k_h\ell)=-(h\ell)({\ell}k_h)=((h\ell)\ell)k_h=-hk_h=-k \\
i_{h\ell}h_{\ell}&=(i_h\ell)(h\ell)=-(i_h\ell)({\ell}h)=((i_h\ell)\ell)h=-i_hh=i \\
i_{h\ell}^2&=-1 \\
i_{h\ell}j_{h\ell}&=(i_h\ell)(j_h\ell)=-(i_h\ell)({\ell}j_h)=((i_h\ell)\ell)j_h=-i_hj_h=k \\
i_{h\ell}k_{h\ell}&=(i_h\ell)(k_h\ell)=-(i_h\ell)({\ell}k_h)=((i_h\ell)\ell)k_h=-i_hk_h=-j \\
j_{h\ell}h_{\ell}&=(j_h\ell)(h\ell)=-(j_h\ell)({\ell}h)=((j_h\ell)\ell)h=-j_hh=j \\
j_{h\ell}i_{h\ell}&=(j_h\ell)(i_h\ell)=-(j_h\ell)({\ell}i_h)=((j_h\ell)\ell)i_h=-j_hi_h=-k \\
j_{h\ell}^2&=-1 \\
j_{h\ell}k_{h\ell}&=(j_h\ell)(k_h\ell)=-(j_h\ell)({\ell}k_h)=((j_h\ell)\ell)k_h=-j_hk_h=i \\
k_{h\ell}h_{\ell}&=(k_h\ell)(h\ell)=-(k_h\ell)({\ell}h)=((k_h\ell)\ell)h=-k_hh=k \\
k_{h\ell}i_{h\ell}&=(k_h\ell)(i_h\ell)=-(k_h\ell)({\ell}i_h)=((k_h\ell)\ell)i_h=-k_hi_h=j \\
k_{h\ell}j_{h\ell}&=(k_h\ell)(j_h\ell)=-(k_h\ell)({\ell}j_h)=((k_h\ell)\ell)j_h=-k_hj_h=-i \\
k_{h\ell}^2&=-1 \\
\end{align}

プログラム

計算過程は以下のプログラムで生成しました。手順探索などは一切なく、手作業で分類したパターンマッチで処理しています。

Sedenion.fs

type Sedenion =
    E | I | J | K | H of Sedenion | L of Sedenion

    override x.ToString() =
        match x with
        |   E -> "1" | I -> "i" | J -> "j" | K -> "k"
        | H E -> "h"
        | H x -> string x + "_h"
        | L E -> @"{\ell}"
        | L (H E) -> @"h_{\ell}"
        | L (H x) -> string x + @"_{h\ell}"
        | L x -> string x + @"_{\ell}"

    member x.Next =
        match x with
        |   I -> J
        |   J -> K
        |   K -> I
        | H x -> H x.Next
        | L x -> L x.Next
        |   x -> x

let right (s:string) = s.Substring(s.LastIndexOf '=' + 1)

let rec prod sgn x y =
    let sx, sy = string x, string y
    let left = sgn + sx + sy + if sgn = "" then "&=" else "="
    let inv = if sgn = "-" then "" else "-"
    match x, y with
    | _, E -> sx
    | E, _ -> sy
    | x, y when x = y -> sx + "^2&=-1"
    | L x, L E ->
        // (xℓ)ℓ=-x
        left + sgn + "(" + string x + @"\ell)\ell=" + inv + string x
    | L E, L _ -> left + prod inv y x
    | L x, L y ->
        // (xℓ)(yℓ)=-(xℓ)(ℓy)=((xℓ)ℓ)y=-xy
        let sx, sy = string x, string y
        let result = prod sgn y x |> right
        sprintf "%s%s(%s\ell)(%s\ell)=%s(%s\ell)({\ell}%s)=%s((%s\ell)\ell)%s=%s%s%s=%s"
                left  sgn sx sy  inv sx sy  sgn sx sy  inv sx sy  result
    | L _, H _ -> left + prod inv y x
    | H E, L (H E) -> left + sgn + @"h(h\ell)=" + inv + @"\ell"  // h(hℓ)=-ℓ
    | H E, L (H y) ->
        // h((yh)ℓ)=-(h(yh))ℓ=((yh)h)ℓ=-yℓ
        let sy = string y
        sprintf @"%s%sh((%sh)\ell)=%s(h(%sh))\ell=%s((%sh)h)\ell=%s%s\ell=%s%s_{\ell}"
                left  sgn sy  inv sy  sgn sy  inv sy  inv sy
    | H E, L E -> left + sgn + @"h_{\ell}"  // hℓ
    | H E, L y ->
        // h(yℓ)=-(hy)ℓ=(yh)ℓ
        let sy = string y
        sprintf @"%s%sh(%s\ell)=%s(h%s)\ell=%s(%sh)\ell=%s%s_{h\ell}"
                left  sgn sy  inv sy  sgn sy  sgn sy
    | H x, L (H E) ->
        // (xh)(hℓ)=-((xh)h)ℓ=xℓ
        let sx = string x
        sprintf @"%s%s(%sh)(h\ell)=%s((%sh)h)\ell=%s%s\ell=%s%s_{\ell}"
                left  sgn sx  inv sx  sgn sx  sgn sx
    | H x, L (H y) when x = y ->
        // (xh)((xh)ℓ)=-ℓ
        left + sgn + sx + "(" + string (H y) + @"\ell)=" + inv + @"\ell"
    | H x, L (H y) ->
        // (xh)((yh)ℓ)=-((xh)(yh))ℓ=-(yx)ℓ
        let sgn2, yx = if y.Next = x then inv, x.Next else sgn, y.Next
        let sy, syx = string (H y), string yx
        sprintf @"%s%s%s(%s\ell)=%s(%s%s)\ell=%s(%s)\ell=%s%s_{\ell}"
                left  sgn sx sy  inv sx sy  sgn2 syx  sgn2 syx
    | H x, L E -> left + sgn + (string x) + "_{h\ell}"  // (xh)ℓ
    | H x, L y when x = y ->
        // (xh)(xℓ)=-((xh)x)ℓ=(x(xh))ℓ=-hℓ
        let sx2 = string x
        sprintf @"%s%s%s(%s\ell)=%s(%s%s)\ell=%s(%s%s)\ell=%sh_{\ell}"
                left  sgn sx sx2  inv sx sx2  sgn sx2 sx  inv
    | H x, L y ->
        // (xh)(yℓ)=-((xh)y)ℓ=-((yx)h)ℓ
        let sgn2, yx = if y.Next = x then inv, x.Next else sgn, y.Next
        let sy, syx = string y, string yx
        sprintf @"%s%s%s(%s\ell)=%s(%s%s)\ell=%s(%sh)\ell=%s%s_{h\ell}"
                left  sgn sx sy  inv sx sy  sgn2 syx  sgn2 syx
    | _, L (H E) ->
        sprintf @"%s%s%s(h\ell)=%s(%sh)\ell=%s%s"
                left  sgn sx  inv sx  inv (string (L (H x)))
    | x, L (H y) when x = y ->
        // i((ih)ℓ)=-(i(ih))ℓ=hℓ
        sprintf @"%s%s%s(%s_h\ell)=%s(%s%s_h)\ell=%sh\ell=%sh_{\ell}"
                left  sgn sx sx  inv sx sx  sgn  sgn
    | x, L (H y) ->
        // i((jh)ℓ)=-(i(jh))ℓ=((ij)h)ℓ=(kh)ℓ
        let sy = string (H y)
        let sgn2, xy = if x.Next = y then sgn, y.Next else inv, x.Next
        sprintf @"%s%s%s(%s\ell)=%s(%s%s)\ell=%s%s\ell=%s%s"
                left  sgn sx sy  inv sx sy  sgn2 (string (H xy))  sgn2 (string (L (H xy)))
    | x, L E -> left + sgn + sx + @"_{\ell}"  // xℓ
    | x, L y when x = y ->
        left + sgn + sx + "(" + sx + @"\ell)=" + inv + @"\ell"  // x(xℓ)=-ℓ
    | x, L y ->
        // x(yℓ)=-(xy)ℓ
        let sgn2, xy = if x.Next = y then inv, y.Next else sgn, x.Next
        let sy, sxy = string y, string xy
        sprintf @"%s%s%s(%s\ell)=%s(%s%s)\ell=%s%s\ell=%s%s_{\ell}"
                left  sgn sx sy  inv sx sy  sgn2 sxy  sgn2 sxy
    | H x, H E -> left + sgn + "(" + string x + "h)h=" + inv + string x
    | H E, H _ -> left + prod inv y x
    | H x, H y ->
        // (xh)(yh)=-(xh)(hy)=((xh)h)y=-xy
        let sx, sy = string x, string y
        let result = prod sgn y x |> right
        sprintf "%s%s(%sh)(%sh)=%s(%sh)(h%s)=%s((%sh)h)%s=%s%s%s=%s"
                left  sgn sx sy  inv sx sy  sgn sx sy  inv sx sy  result
    | x, H E -> left + sgn + string (H x)
    | x, H y when x = y ->
        left + sgn + sx + "(" + sx + "h)=" + inv + "h"  // x(yh)=-(xy)h
    | x, H y ->
        // x(yh)=-(xy)h
        let sgn2, xy = if x.Next = y then inv, y.Next else sgn, x.Next
        let sy, sxy = string y, string xy
        sprintf "%s%s%s(%sh)=%s(%s%s)h=%s%sh=%s%s_h"
                left  sgn sx sy  inv sx sy  sgn2 sxy  sgn2 sxy
    | x, y when x.Next = y -> left + sgn + (string y.Next)
    | x, y ->
        if sgn <> "" then "??? " + sx + sy else
        left + prod inv y x

printfn @"\begin{align}"
let elems = [[I; J; K]
             [H E; H I; H J; H K]
             [L E; L I; L J; L K]
             [L (H E); L (H I); L (H J); L (H K)]]
elems |> List.iteri (fun i xs ->
    elems |> List.iteri (fun j ys ->
        for x in xs do
            for y in ys do
                printfn @"%s \\" (prod "" x y)
        if i + j < 6 then printfn @"\hline"))
printfn @"\end{align}"

参考

十六元数で作った物理のトイモデルの紹介記事です。ファノ平面をホルスの目に描く遊び心が良いです。

• Computational Applications Group [T.Raptis]