テキストを意味で検索したり分類したりする際に、埋め込み (embedding) という技術が使われます。本記事では、埋め込みとは何かをなるべく簡単に説明して、実際にモデルを使ってみます。
更新履歴:
- 2024/12/10 22:15 Ruri のプレフィックス
"クエリ: "と"文章: "に対応
埋め込みとは
「埋め込み」という言葉は、「ベクトル空間への埋め込み」という概念に由来します。これは、様々なデータを数値の並び（ベクトル）に変換することを意味します。つまり、ベクトルの世界に「埋め込む」というイメージです。
例えば、平面上の点は $(x, y)$ という2つの数値で表現できますが、これは 2 次元のベクトル空間への埋め込みと考えることができます。同様にテキストや画像などのデータも、より多くの数値を使ってベクトルに変換できます。
テキストのベクトル化
例えば、「今日は良い天気です」という文章は、$(0.12, -0.34, 0.56, \cdots)$ のようなベクトルに変換されます。
このとき重要なのは、似たような意味を持つ文章は似たようなベクトルになるという性質です。「今日は晴れています」という文章は、「今日は良い天気です」に似たベクトルに変換されます。
天気とは無関係な「今日はゴミの日です」という文章は、「今日は良い天気です」や「今日は晴れています」とはあまり似ていないベクトルに変換されます。
このようにベクトル同士がどれだけ似ているかを計算することで、似ているデータを見つけることができます。これを利用して検索や推薦を行うことが可能です。また、似たベクトルをグループ化することで、データのクラスタリングを行うこともできます。
ベクトルの方向
ベクトルを矢印として考えれば、サイズが 0 でなければ何らかの方向を指しています。テキストを埋め込む場合、ベクトルの長さではなく方向に意味を持たせます。
つまり、2 本のベクトルが似ているかどうかは、方向がどれだけ近いか、言い換えればベクトル間の角度によって判定できます。ただし、実用的には角度の計算よりも簡単な方法で代用できます。それについて必要となる事項を説明します。
内積
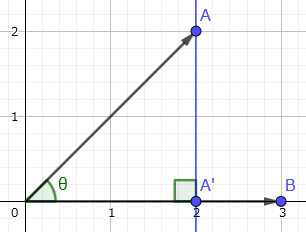
2 本のベクトル A, B を考えます。A から B へ垂線を下ろして、交点を A' とします。
A を縮めて B と同じ方向に向けたベクトルを A' と考えます。A' と B の長さの積を、A と B の内積と呼びます。上例では $2×3=6$ です。
逆に、B から A に垂線を下ろして内積を計算しても、結果は一致します。
$$
\frac32\sqrt2×2\sqrt2=6
$$
つまり、どちらからどちらに垂線を下ろすかに関係なく、方向を揃えて長さの積を計算したものが内積です。
A の長さを $|A|$、A と B の間の角度を $θ$ とすれば、A' の長さは $|A'|=|A|\cosθ$ となります。この計算を使えば、どちらからどちらに垂線を下ろしても同じ結果になることが直感的に分かります。
$$
(|A|\cosθ)|B|=|A|(\cosθ|B|)
$$
内積は成分からも計算できます。A と B の $x$ 成分同士の積と $y$ 成分同士の積を計算して、それらを足します。
$$
A(2,2),B(3,0)\ →\ 2×3+2×0=6
$$
内積は成分を使えば簡単に計算できるというのがポイントです。なぜこの計算方法が成り立つかは、以下の記事を参照してください。
コサイン類似度
テキストを埋め込んだベクトルは、長さではなく方向に意味があります。計算を簡単にするため、長さはすべて 1 になるように正規化します。
A と B を長さ 1 のベクトルとすれば、$|A|=|B|=1$ となります。A と B の間の角度を $θ$ とすれば、A と B の内積は $\cosθ$ となります。$\cosθ$ の値の範囲は -1～1 で、方向が一致すれば最大値 $\cos0=1$ となるため、値が大きい（1 に近い）ほど角度 $θ$ が小さいと判断できます。
つまり、2 本のベクトルの方向がどれだけ近いかは、ベクトル間の角度を求めなくても、内積の計算により求めたコサインの値で判断できます。これをコサイン類似度と呼びます。
既に見たように、内積の計算は、同じインデックスの成分同士の積を計算して、それらを足すだけのため、角度を求めるよりもずっと簡単です。後で見るように、ベクトルを使った検索では大量の類似度を計算する必要があるため、計算が簡単であることは重要です。
なお、計算方法から分かるように、ベクトルの次元（数値の個数）は一致している必要があります。
テキスト埋め込みモデル
テキストを、方向が意味を持つようなベクトルに変換するように訓練されたモデルをテキスト埋め込みモデルと呼びます。
本記事では、最近リリースされた日本語対応のテキスト埋め込みモデル Ruri を使用します。
使い方
実際に Python で使ってみます。uv の利用を前提とします。
uv を初期化して、必要なライブラリをインストールします。
uv init
uv add sentence-transformers fugashi unidic_lite
以下、REPL での利用を想定してプロンプト >>> を付けますが、この部分は入力しないでください。
モデルを読み込みます。
>>> from sentence_transformers import SentenceTransformer
>>> model = SentenceTransformer("cl-nagoya/ruri-base")
初回利用時に Hugging Face から自動的にダウンロードされますが、次回からはキャッシュが使われます。
テキストをベクトルに変換します。
>>> v = model.encode("文章: 変換したい文章")
【追記】文章: の部分は Ruri 特有のプレフィックスです。他のモデルでは不要です。
ベクトルの次元を確認します。
>>> len(v)
768
自分自身との内積の平方根によって、ベクトルの長さを確認します。
>>> import math
>>> math.sqrt(v.dot(v))
18.60057565762205
v.dot(v) は v と v の内積です。角度は 0 のため $\cos 0=1$ です。よって内積は $|v|^2$ となり、平方根によって長さが求まります。
変換時に正規化を指定すれば、長さは約 1 になります。
>>> v = model.encode("文章: 変換したい文章", normalize_embeddings=True)
>>> math.sqrt(v.dot(v))
0.9999999403953534
多少の誤差がありますが、影響は無視できます。
類似度の計算
複数のベクトルを一度に変換します。
>>> texts = ["今日は良い天気です", "今日は晴れています", "今日はゴミの日です"]
>>> vs = model.encode(["文章: " + t for t in texts], normalize_embeddings=True)
内積（コサイン類似度）を計算します。
>>> vs[0].dot(vs[1])
np.float32(0.95302933)
>>> vs[0].dot(vs[2])
np.float32(0.8644165)
>>> vs[1].dot(vs[2])
np.float32(0.8722215)
「今日は良い天気です」と「今日は晴れています」が最も類似しており、「今日はゴミの日です」はあまり類似していないと判定されました。
ベクトル検索
ある程度の長さのテキストを適当な長さで区切ってベクトル化して、指定したベクトルと類似度でランク付けして上位を抽出する操作をベクトル検索と呼びます。必ずしも単語が一致しなくても、意味的に近いテキストを検索することができます。
区切り方は様々なパターンがあり、実用的なベクトル検索システムを構築する上では重要です。本記事では実用性よりも直感的な結果を得ることを優先して、文単位で区切ります。
事前に文単位で改行されたテキストを用意しました。
このテキストに対するベクトル検索システムを実装します。
実装
使用するファイルを設定します。
textfile = "all-ja-gemini-lines.md"
tensorfile = "vectors.safetensors"
テキスト埋め込みモデルを読み込みます。
from sentence_transformers import SentenceTransformer
model = SentenceTransformer("cl-nagoya/ruri-base")
テキストをベクトル化する関数を定義します。コサイン類似度の計算は PyTorch のライブラリを利用するため、仕様に合わせて 1 要素のリストとして、convert_to_tensor=True で PyTorch 形式を指定します。
def embed(text):
return model.encode([text], normalize_embeddings=True, convert_to_tensor=True)
テキストファイルを読み込みます。空行はスキップします。行番号を保持して、後で検索結果の表示に使用します。
with open(textfile, "r", encoding="utf-8") as f:
lines = [(i, l) for i, line in enumerate(f, 1) if (l := line.strip())]
テキストファイルの各行をベクトル化します。この処理は時間がかかるため、結果をファイルに保存し、次回からは保存したデータを使用します。
import os, torch, safetensors.torch
if os.path.exists(tensorfile):
# 保存済みの数値データを読み込み
tensor = safetensors.torch.load_file(tensorfile)["lines"]
else:
from tqdm import tqdm
# 新規にベクトル化して保存
test = embed("test")[0] # ベクトルサイズの確認用
tensor = torch.zeros(len(lines), len(test), dtype=torch.float32)
for i, (_, line) in tqdm(enumerate(lines), total=len(lines)):
tensor[i, :] = embed("文章: " + line)[0]
safetensors.torch.save_file({"lines": tensor}, tensorfile)
実際の検索を行う関数を実装します。コサイン類似度の計算に PyTorch の関数を使用します。これにより、指定したベクトルと、変換済みのすべてのベクトルとの類似度が一気に計算できます。ベクトル検索では上位 K 件（ここでは 10 件）を取得します。これを TopK 検索と呼びます。
import torch.nn.functional as F
def search(query):
emb = embed("クエリ: " + query)
# コサイン類似度の計算
similarities = F.cosine_similarity(tensor, emb, dim=1)
# TopK 検索（上位 10 件を取得）
for i, (value, index) in enumerate(zip(*torch.topk(similarities, k=10)), 1):
value, index = value.item(), index.item() # 数値に変換
lnum, line = lines[index]
yield len(emb[0]), i, value, lnum, line
【追記】クエリ: の部分は Ruri 特有のプレフィックスです。他のモデルでは不要です。
これで実装は完了です。対話的なインターフェースで検索を試してみましょう。スコアが 1 に近いほど、入力した文章に意味が近いことを示します。
while True:
print()
try:
query = input("> ")
except:
print()
break
for _, i, v, lnum, line in search(query):
print(f"{i:2d}: {v:.5f} {lnum:4d} {line}")
$ uv run test.py
100%|███████████████████████████████████████████████| 4497/4497 [02:50<00:00, 26.31it/s]
> 楽器について
1: 0.86019 621 「あなたはシタールを弾くことができますか？」
2: 0.84824 1197 そう言って、彼は小さなシタールのペグを回した。
3: 0.84782 5484 あちこちで音楽が鳴り響いている。
4: 0.84511 624 そしてすぐにシタールを手に取った。
5: 0.84411 2566 もうシタールは弾きません。
6: 0.83964 4135 ハーン・サヘブ「あなたはもうそのシタールを弾かないのですか？あなたのそのシタールはどこにあるのですか？ 」
7: 0.83921 2565 「このシタールを置いていきます、兄さん。
8: 0.83699 628 彼は立ち上がって演奏し始めた。
9: 0.83270 2914 その音が彼の唯一の仲間となり、その絶え間ない単調な音が、彼の躍動する情熱のリズムに合わせて拍手を送りま した。
10: 0.83250 2559 しかし、ビバの涙を見て、シタールの演奏が妨げられるようになった。
モデルの対応言語
テキスト埋め込みモデルは、学習時に使用された言語でしか正しく機能しません。対応言語で書かれた文章であれば、その意味を適切にベクトル化できますが、対応していない言語の文章は、意味を正しく捉えることができません。
モデルが言語に対応しているかどうかは、実際にテキストを入力して調べるのが最も確実です。対応していない言語の場合、以下のような現象が発生します。
- 似た意味の文章でも、類似度が極端に低くなる
- 意味が全く異なる文章なのに、高い類似度を示す
- 文字単位や記号での一致に偏った結果を返す
したがって、使用する言語に対応したモデルを選択することが非常に重要です。
実験例
以下に、様々なモデルで実験した例があります。日本語に対応していないモデルがどのような挙動を示すか確認できます。
| モデル | 対応言語 |
|---|---|
| jinaai/jina-embeddings-v2-base-zh | 中国語 |
| intfloat/multilingual-e5-large | 日本語を含む多言語 |
| BAAI/bge-m3 | 日本語を含む多言語 |
| cl-nagoya/ruri-base | 日本語 |
| それ以外 | 英語 |
- 日本語対応モデルでも結果は一致しておらず、モデル間に性能差がある
- 英語対応モデルではまともに検索できない
- 中国語対応モデルでは一部の漢字が中国語の意味で評価された結果、多少は意味が通じているように見える
Ruri 登場以前は、上の実験で使用した multilingual-e5-large や bge-m3 がよく使われていたようです。埋め込みで Ollama を使用する場合、選択肢に bge-m3 があればそれを使うのが無難なようです。（👉参考）
ベクトルデータベース
本記事では、テキストから変換したベクトルを safetensors ファイルに保存する単純な方法を採用しました。しかし対象となるドキュメントの規模が大きくなると、このような単純な方法では対応しきれなくなります。
大規模なベクトルデータを管理するシステムとしてベクトルデータベース（Chroma など）があります。実用的なベクトル検索システムを構築するには、ベクトルデータベースの導入は不可欠です。
参考
テキストから埋め込みベクトルへの変換は情報が欠損するため、元のテキストを完全には復元できないようです。
テキストを埋め込み表現に変換する話はよくあるけど、逆に埋め込みからテキストを復元する論文見つけて読んでみた。
— goto (@goto_yuta_) October 30, 2024
ニューラルの層は高次元の表現をするけど、非線形層が情報を部分的に破壊して、結果的に情報量は維持or減少する(言われてみれば当然な)から入力情報量の完全保持は不可能なんだと。 pic.twitter.com/p4ECPleXNh
論文によれば、32 トークンの入力テキストの復元率は 92% のようです。
re-embeds text is able to recover 92% of 32-token text inputs exactly.