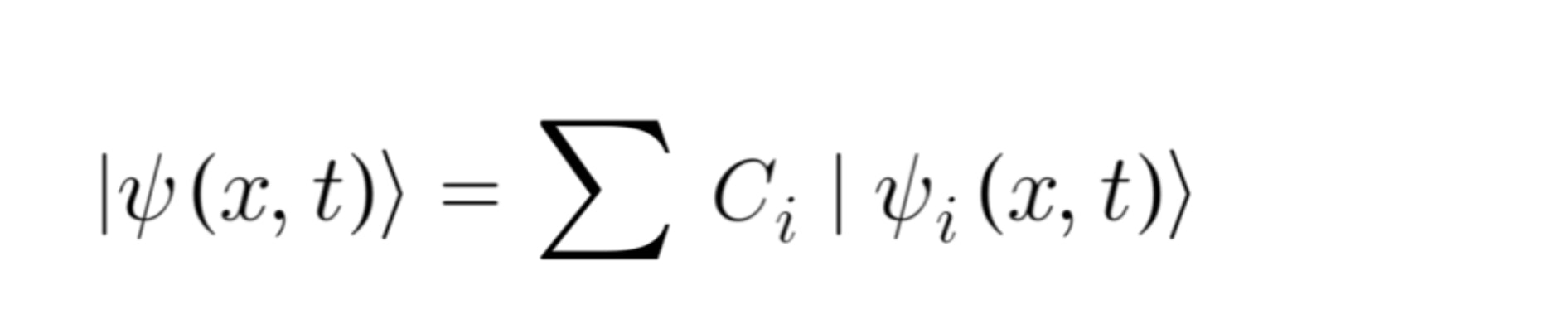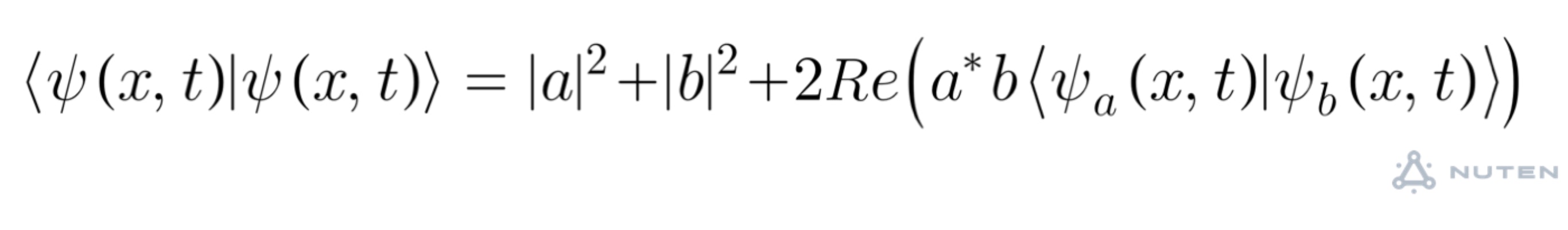【Python】時間発展する箱の中の粒子

時間発展する箱の中の粒子を書きました

時間発展する箱の中の粒子を描いた 0≦x≦π
ψ(x,t) = 0.9φ1(x,t) + 0.1φ2(x,t) pic.twitter.com/vK4TACGhOD

— カルバニオン (@78910jqk13) July 25, 2018

おもに参考にさせていただいた文献は

入門 量子ダイナミクス(上) 時間依存の量子力学を中心に
David J. Tannor (原著), 山下 晃一 (翻訳)
です。
Python3.6.3で書きました。

説明

時間に依存するSchrödinger方程式

を満たすψはこれらの線形結合

も

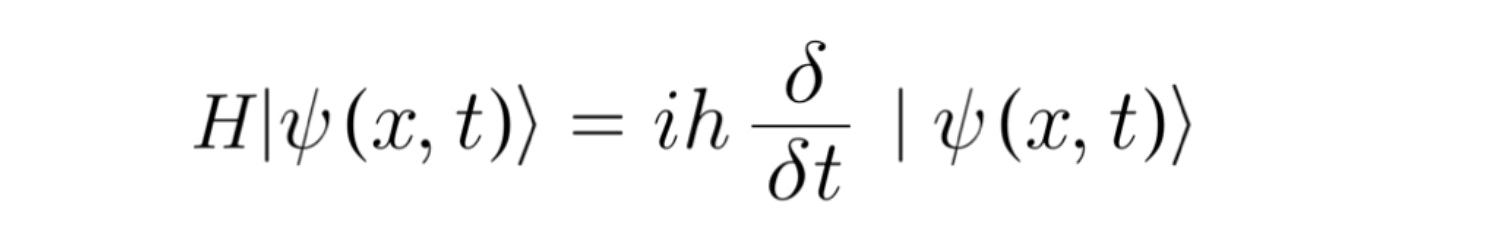
を満たします。
というわけで、0≦x≦πの箱の中の粒子のn=1のときの解をφa、n=2のときの解をφbとして、これら２つの線形結合

の確率存在密度

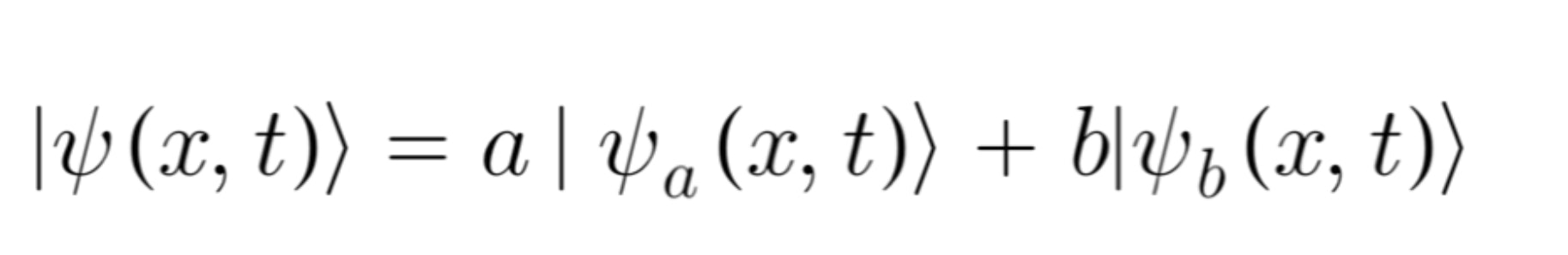
をグラフにしてみました。
今回はa=0.9,b=0.1としました。

コード

mixture.py

import matplotlib
matplotlib.use("Agg")
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

time,x = np.mgrid[-3.141592:3.141592:40j,0:3.1415:100j]
wavefunction1 = 1.414213 * np.sin(x) * np.exp(-1j * time)
wavefunction2 = 1.414213 * np.sin(2 * x) * np.exp(-4j * time)
wave_mixture = 0.9 * wavefunction1 + 0.1 * wavefunction2
probability_density_wave_mixture = np.conj(wave_mixture) * wave_mixture

#plot
fig = plt.figure()

imgs = []

for i in range(40):
	img = plt.plot(x[i],np.real(probability_density_wave_mixture[i]), linewidth =4, color="#2e0fc1")
	imgs.append(img)
	

ani = animation.ArtistAnimation(fig, imgs, interval=70)
ani.save("output3.gif", writer="imagemagick")

作業環境

Debian 4.9.82
Python3.6.3 Anaconda

またgifの保存にはImagemagickを入れる必要があります。

sudo apt-get install imagemagick

参考にさせていただいた本、サイト

入門 量子ダイナミクス(上) 時間依存の量子力学を中心に
David J. Tannor (原著), 山下 晃一 (翻訳)

matplotlib でアニメーションを作る

【python】水素様原子のpx軌道の存在確率密度plot