【python】水素様原子のpx軌道の存在確率密度plot

概要

どんな教科書にもだいたい載ってる水素様原子の電子のpx軌道の存在確率密度をプロットしてみました。

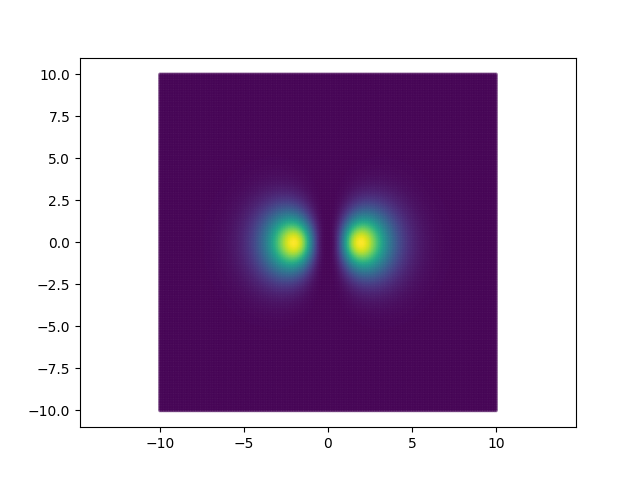
非相対論的なSchrödinger方程式の特殊解の一つに基づいて、具体的には、Wikipediaの水素原子におけるシュレーディンガー方程式の解に基づいて $ \psi {111} $ のplotです。
実際はこんな軌道を電子がこんな確率密度分布をしているわけではないのですが

方法

まずxz平面に格子点をとります。
格子点(x,z)に依存した値(存在確率密度 $ | \psi {111} | ^ 2 $ )に応じて、色をつけて、散布図としてプロットしました。

水素原子におけるシュレーディンガー方程式の解は極座標で記述されているため、直交座標でとった格子点を一回極座標に移してから存在確率密度 $ | \psi {111} | ^ 2 $ をとっています。

コード

scatter.py

import matplotlib
matplotlib.use(‘Agg’)
import matplotlib.pyplot as plt
import numpy as np

x,y,z = np.mgrid[-10:10:200j,-0:0:1j,-10:10:200j]

r = (x ** 2 + y ** 2 + z ** 2 ) ** 0.5
t = np.arccos(z / ((x ** 2 + y ** 2 + z **2 ) ** 0.5
))
p = np.arccos(x / (x**2)**0.5)

den_r = r * np.exp(-r)
den_t = np.sin(t)
den_p = np.cos(p)

density =( den_r * den_t * den_p )** 2   * r ** 2 * np.sin(t)

plt.axis(‘equal’)
plt.scatter(x,z, s=3, c=density, alpha=.5)

plt.savefig(“scatter.png”)