jupyter notebook コードはこちら!(https://github.com/29Takuya/wvae)
0. 背景
こんにちは、@29Takuyaです。(プロフィールページ)
突然ですが、普段私たちが目にするデータは様々な要素(潜在変数)から構成されます。
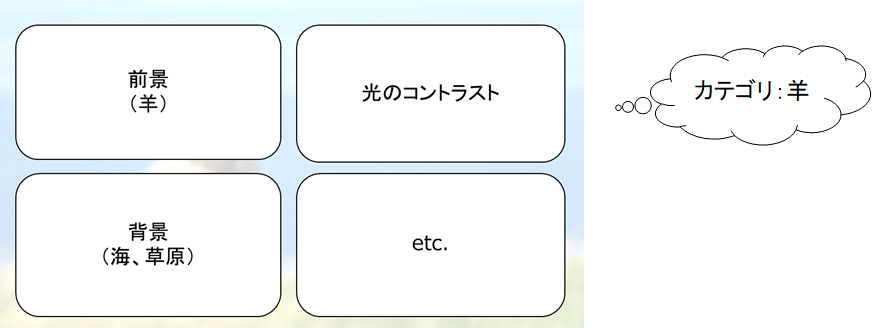
例えば、以下の画像を見て下さい。

おそらく多くの人はまず「羊」というワードを思い浮かべるでしょう。
しかし、この画像には他にも様々な情報が含まれています。
例えば背景であり、天気であり、より具体的な羊の種類であったりします。
そのような、観測されるデータを構成している要素をここでは潜在変数と呼びます。
今回の目標は、あるラベルが利用可能な場合に、入力を「ラベルに関係する潜在変数」と「その他の潜在変数」に分解することです。
いくつかの例を挙げます。
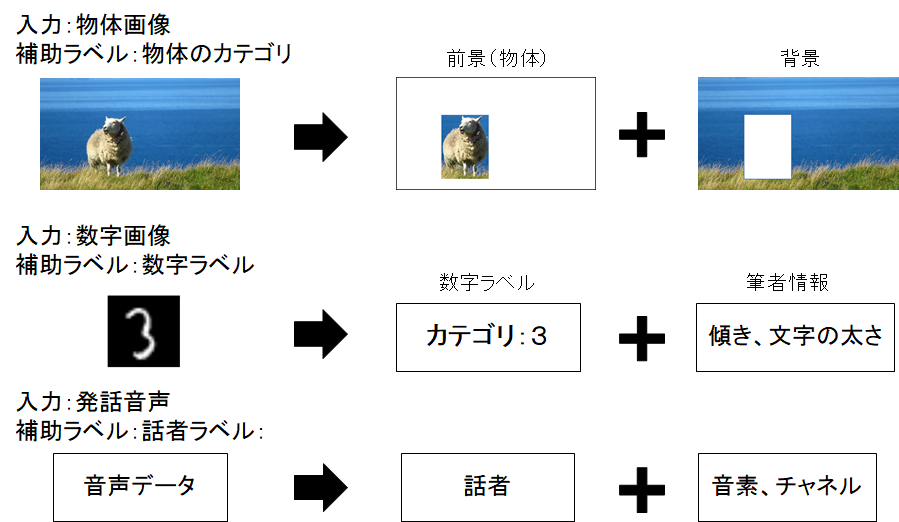
- 物体が写っている画像を前景と背景の変数に分解
- 数字画像を数字情報と筆者情報に分解
- 発話音声を音韻性と話者性に分解
もしこのような分解が可能であれば、識別に関係のない要素(音声認識であれば話者性)を取り除くことができるのではないかと考えました。
1. 問題設定
今回は手書き数字画像を、数字ラベルを利用することで、「数字情報」と「その他(筆者情報など)」に分類することを目指します。
イメージは、画像を「数字性を表す軸」と「その他の情報を表す軸」の空間にプロットするような感じです。

2. 提案モデル
ベースはVAE(Variational Autoencoder)なのですが、普通のVAEと違う点は、中間層が2つのボトルネックに分かれていることです。
片方の中間層には、Classifierを繋げて数字ラベルを予測します。
- Latent Variable A には識別器を繋げることで、数字の識別に効果的な潜在変数になることを期待しています。
- Latent Variable B には識別的な制約が無いため、識別に必要ではないが復元には必要な情報が詰まっていることを期待します。
3. 実験
今回の実験には、EMNIST(MNISTの拡張)というデータセットを用いました。
MNISTと異なるのは、数字ラベル以外(筆者ラベルなど)も利用できるという点です。
EMNISTデータセット
- 数字画像(28×28)+筆者ラベル
- Train: 240000 images
- Test : 40000 images
- 筆者数:3579人 一人あたり 50~100枚程度
- TrainとTestに含まれる筆者は同じ
実験Ⅰ(潜在表現の可視化)
実験の目的
潜在変数をそれぞれ1次元で学習させてみて、潜在空間がどのようになっているか可視化します。
実験結果
学習をさせてみて、潜在変数を平面(横軸:Latent Variable A, 縦軸:Latent Variable B)にプロットした結果が以下になります。
- 上の画像:テストデータから得た潜在変数をプロットし、数字ラベルで色付けしたもの。
- 下の画像:潜在空間から1点を選び、復元したもの(座標系は上の画像と対応しています。)
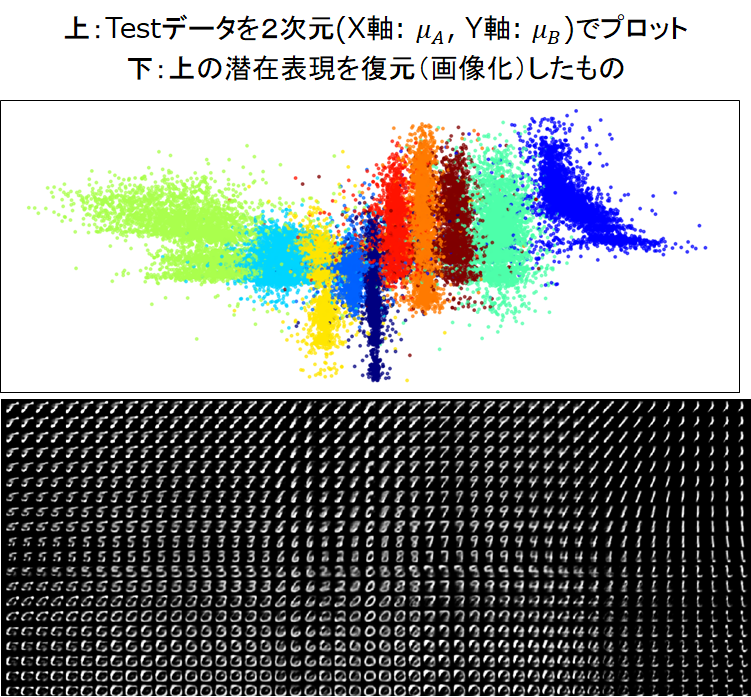
これらの画像から言えることは以下の2点です。
- 横軸(Latent Variable A)が数字ラベルに関して識別的になっている
- 下の画像を見ると、縦軸(Latent Variable B)には、文字の傾きのような表現が得られている
Latent Variable Bが筆者情報を表す潜在変数となっているとは断言できませんが、画像を構成する数字ラベル以外の情報が含まれていると考えることができるのではないでしょうか。
実験Ⅱ(筆者クラスタリング)
実験の目的
実験Ⅰで数字画像から筆者らしき情報(Latent Variable B)が得られました。
この潜在変数を利用して、筆者のクラスタリングを行ってみます。
EMNISTには3000人以上の筆者が含まれているので、もう少し筆者数を絞ったデータセットを作りました。
筆者数を絞ったEMNISTデータセット
- Train: 8670 images
- Test: 1030 images
- 筆者:100人 一人あたり 60~100枚程度
- TrainとTestに含まれる筆者は同じ
今回は、それぞれのLatent Variableを10次元に設定しました。
実験Ⅰと同様に学習を行い、潜在変数をT-SNEで2次元に圧縮した結果を以下に示します。
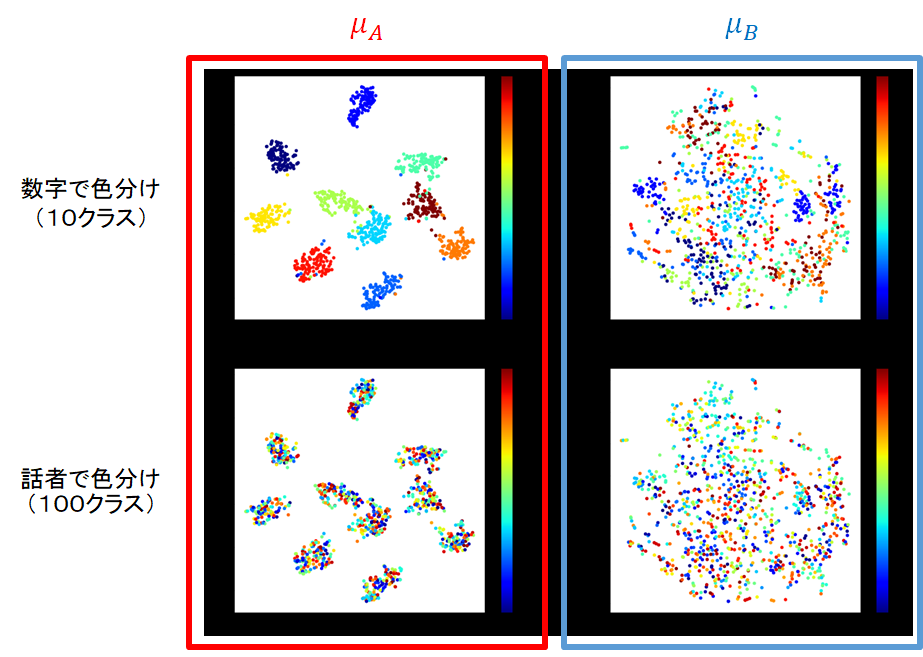
Latent Variable Aは数字できれいに分かれています。
一方、Latent Variable Bは数字の情報は除去されていますが、話者で分かれているということも無いような気がします。
何はともあれ、一度クラスタリングしてみることにしました。
比較手法
| # | Model | Feature Space |
|---|---|---|
| 1 | K-Means (K=100) | Raw Pixcel (784 dim.) |
| 2 | GMM (n_components=100) | Raw Pixcel (784 dim.) |
| 3 | K-Means(K=100) | Latent Variable B (10 dim.) |
| 4 | GMM (n_components=100) | Latent Variable B (10 dim.) |
評価指標
今回はクラスタリングに用いられる以下の3つの指標を用いました。
いずれも値が大きいほうが良いクラスタリングができていることを示します。
- Purity
- Adjusted Rand Score(チャンスレート:0, Perfect:1)
- Adjusted Mutual Info Score(チャンスレート:0, Perfect:1)
実験結果
| # | Purity Score | Adjusted Rand Score | Adjusted Mutual Info Score |
|---|---|---|---|
| 1 | 0.1893 | 0.0204 | 0.0580 |
| 2 | 0.1660 | 0.0153 | 0.0506 |
| 3 | 0.1971 | 0.0275 | 0.0736 |
| 4 | 0.1883 | 0.0220 | 0.0621 |
いずれの指標においても手法3が一番良い精度を出せていることが確認できました。
4. まとめ
VAEを用いて、数字画像の潜在変数を分解することを試みました。
今回は手書き数字画像のデータセットを用いましたが、そもそも筆者認識は難しいタスクであることが知られています。
そのため、今後は合成データなど、もう少し易しいタスクにこのモデルを適用してみたいと考えています。
ここまで読んでいただいてありがとうございました!
