はじめに
こんにちは、現在0からPythonを学んでいる初心者エンジニアです。
この投稿は私が学んだことのアウトプットの場として、そして私と同じ初心者エンジニアさんの少しでも役に立てればと思い、投稿しています。私自身も全くの初心者なので、感想やアドバイスあれば、気軽にコメント頂けると幸いです。
サポートベクタマシンとは
今回はサポートベクタマシンによるハードマージンのマージン最大化に関して記事を書きたいと思います。サポートベクタマシンとは、教師ありデータに対して認識性能が比較的高くよく用いられているパターン認識の一つです。パターン認識に関しては「0からはじめるPython ~パターン認識とは~」を参照してください。サポートベクタマシンの特徴としては、線形分離できない問題に対処できること、また、ふたつのクラスの一部が混入している領域を分離できることなどがあげられます。
クラス分類の方法(マージン最大化)
2クラスに属するデータの特徴量が$x_1とx_2$で表される場合を考えます。この特徴量が平面上におかれた時、下図のように丸と四角で表された二つのクラスを直線$L_1$で分離することをクラス分類といい、この時の直線をクラス分類線といいます。
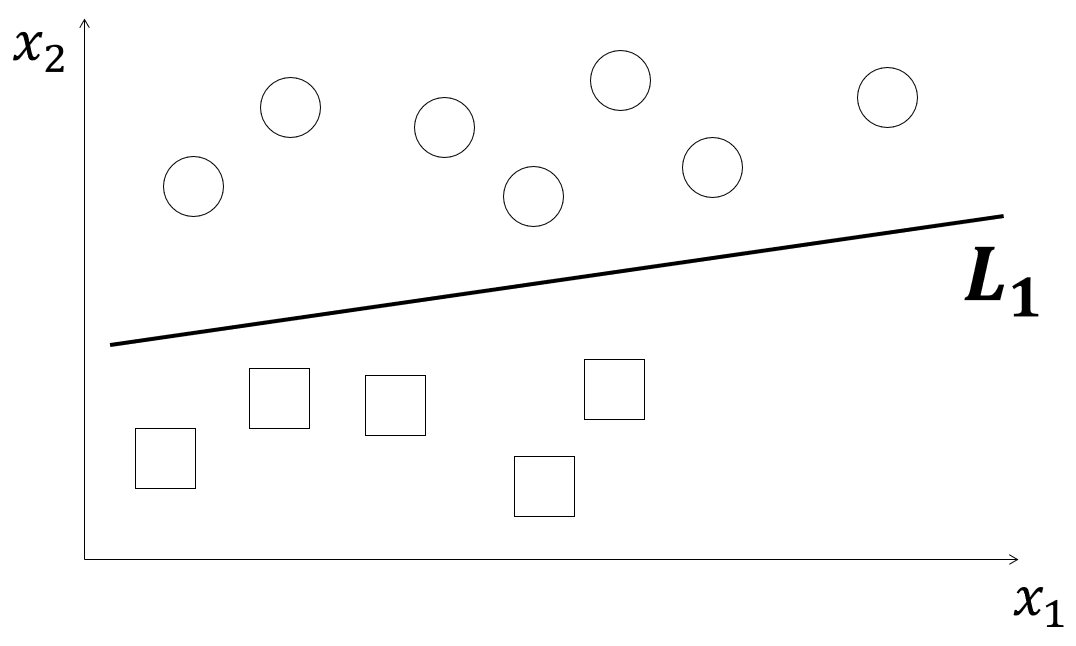
そしてこの直線の推測方法にマージン最大化が挙げられます。
マージン最大化とはクラス分類線とそれに最も近いトレーニングデータ点(サポートベクタ)までの距離(マージン)を最大化することを意味します。マージン最大化の目標は、このマージンをできるだけ大きくすることで、クラス分類線の決定において、より汎化性能を高めることです。つまり、トレーニングデータに対して最適なクラス分類線を見つけることで、未知のデータに対しても高い予測精度を実現することができます。
例えば、下図のようにクラス分類線の候補$L_1とL_2$が存在したとします。この二つの候補のマージンを調べると$B_1とB_2となり、B_1$の方がマージンが広いので$L_1$をクラス分類線として定義します。
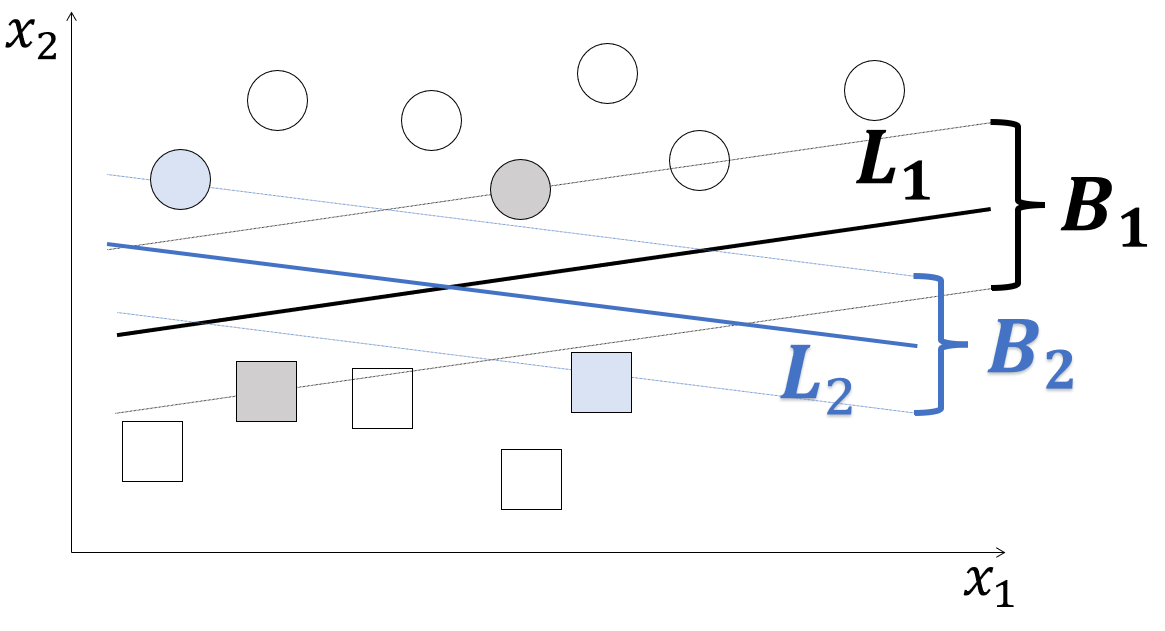
この図のように、クラスをクラス分類線で完全分離できる分類方法をハードマージンと呼び、完全分離できない事例を扱う分類方法をソフトマージンといいます。
なお、このクラス分類線を、パターン認識分野ではしばしば超平面と称するのでこの呼び方も覚えておくと良いです。
ハードマージン最大化の式化
ハードマージンのにおいて、どのようにマージン最大化を行うかを式を用いて説明します。尚、ライブラリを用いればクラス分類を行うことは可能なので、この章は興味がなければ読み飛ばして頂いても構いません。
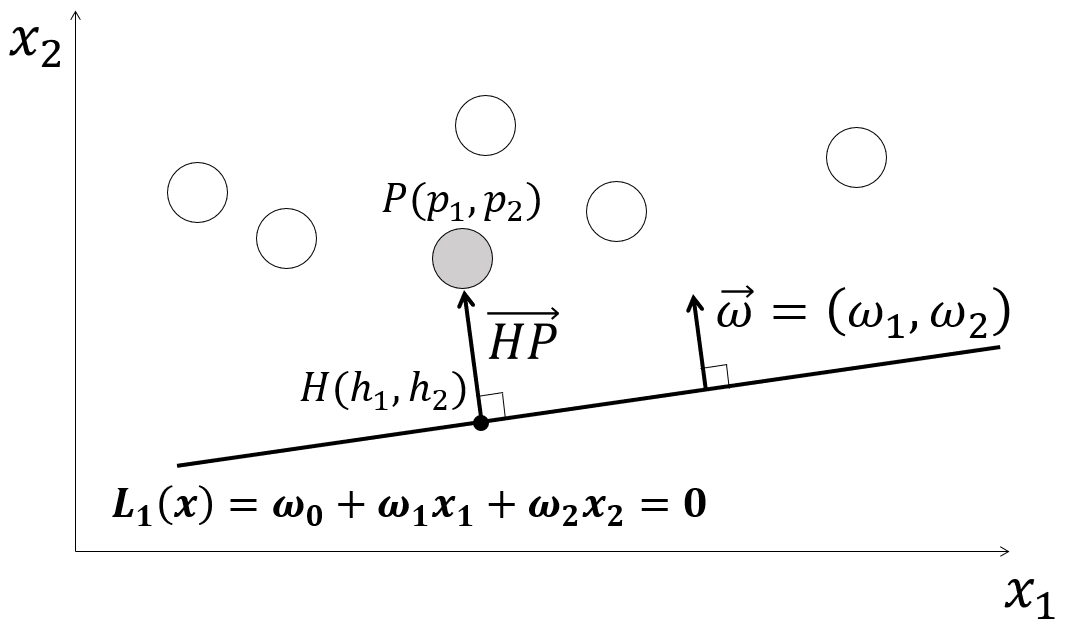
上図のように直線$L_1(x)=\omega_0+\omega_1x_1+\omega_2x_2=0$から最も近いトレーニングデータ点までの法線ベクトルを$\overrightarrow{HP}=(p_1-h_1, p_2-h_2)$とおくと、直線の単位法線ベクトルを$\vec{\omega}=(\omega_1, \omega_2)$とした時
\overrightarrow{HP}=k \vec{\omega}
と表すことができます(kは定数)。
ここで、両辺に$\vec{\omega}$をかけて展開すると
\begin{eqnarray}
\overrightarrow{HP}\cdot \vec{\omega}&=&k \vec{\omega}\cdot \vec{\omega}\\
(p_1-h_1, p_2-h_2)\cdot(\omega_1, \omega_2)&=&k(\omega_1, \omega_2)\cdot(\omega_1, \omega_2)\\
(p_1-h_1)\omega_1+(p_2-h_2)\omega_2&=&k({\omega_1}^2+{\omega_2}^2)\\
\end{eqnarray}
となり、${\omega_1}^2+{\omega_2}^2\neq0$なので、両辺を${\omega_1}^2+{\omega_2}^2$で割ると
k=\frac{(p_1-h_1)\omega_1+(p_2-h_2)\omega_2}{{\omega_1}^2+{\omega_2}^2}
となります。ここで$\vec{HP}$の大きさは
\begin{eqnarray}
\left|\overrightarrow{HP}\right|&=&|k| |\vec{\omega}|\\
&=&\left|\frac{(p_1-h_1)\omega_1+(p_2-h_2)\omega_2}{{\omega_1}^2+{\omega_2}^2}\right|\sqrt{{\omega_1}^2+{\omega_2}^2}\\
&=&\frac{|p_1\omega_1-h_1\omega_1+p_2\omega_2-h_2\omega_2|}{\sqrt{{\omega_1}^2+{\omega_2}^2}}
\end{eqnarray}
ここで$L_1(x)=\omega_0+\omega_1x_1+\omega_2x_2=0$かつ$点H$が直線$L_1(x)$上にあるので
\omega_0=-h_1\omega_1-h_2\omega_2
が成り立つので
\begin{eqnarray}
\left|\overrightarrow{HP}\right|&=&\frac{|p_1\omega_1-h_1\omega_1+p_2\omega_2-h_2\omega_2|}{\sqrt{{\omega_1}^2+{\omega_2}^2}}\\
&=&\frac{|\omega_0+p_1\omega_1+p_2\omega_2|}{\sqrt{{\omega_1}^2+{\omega_2}^2}}\\
&=&\frac{|L_1(p)|}{||\omega||}
\end{eqnarray}
となり、マージンを定式化することができました。
よって、上記の式を用いてマージン最大化を行います。
上図のように$x_1,x_2$平面においてクラス1(丸印)とクラス-1(四角印)があり、それぞれの座標が$x_i=\lbrace x_{1,i}, x_{2,i} \rbrace,(i=1,\cdots,N)$で与えられているとします。
上記の式でクラス分類を行うためにまずは符号関数を次のように導入します。
sgn(u)=
\begin{cases}
{1 \ \;\;\;(u \geq 0)}\\
{-1 \;\;(u< 0)}
\end{cases}
これを用いて、各クラス$x_i$に対するクラス分類を表す$y_i$を次のように定めます。
y_i=sgn\left(L_1(x_i)\right)
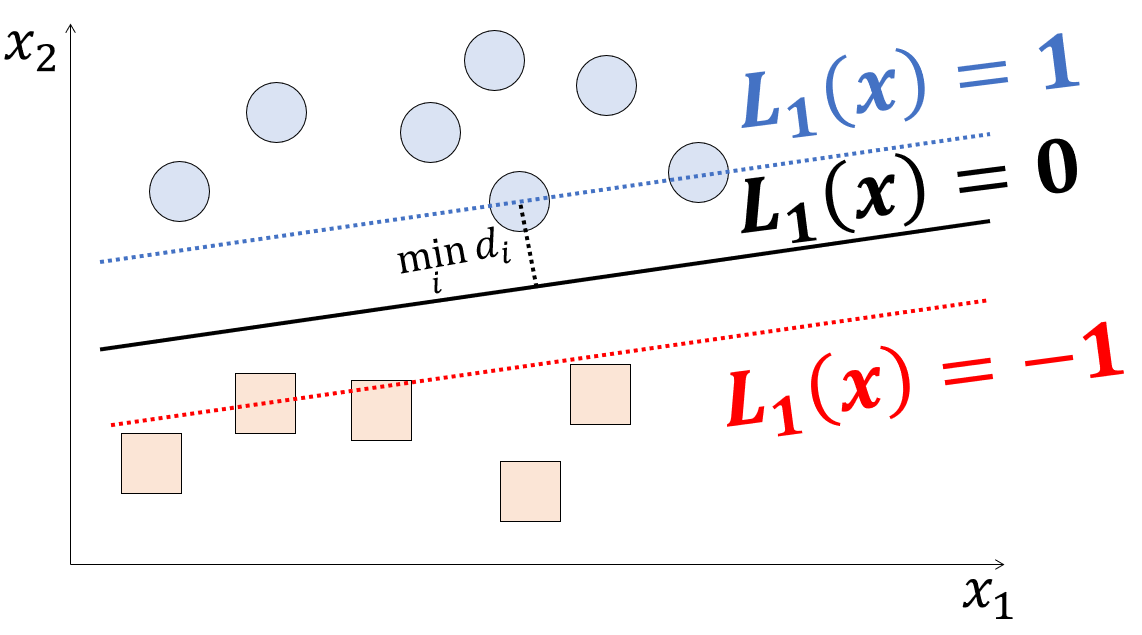
ここで各クラスとの距離$d_iをy_i$を用いて表すと
d_i=y_i\frac{|L_1(x_i)|}{||\omega||}
となり、マージンは最も近いクラスとの距離をとるので、
\min_id_i
を求めることにより、マージンを求めることができます。
ここで、$\omega_0,\omega_1,\omega_2$を同じ定数倍してもクラス分類線(超平面)は変わらないことを考慮し、サポートベクタに対しては
y_iL_1(x_i)=1
という条件をさらに設けると、マージンを最大化するということは
\begin{eqnarray}
arg\max_\omega \left\lbrace \min_id_i \right\rbrace&=&arg\max_\omega \left\lbrace \frac{1}{||\omega||} \right\rbrace\\
&=&arg \min_\omega||\omega||\\
\\subject \; &to& \;\; y_iL_1(x_i)\geq 1
\end{eqnarray}
を求めることと、変換することができます。
この式に2乗形式の最適化問題を解くとき、べき乗の2を相殺するための便宜上の係数$\frac{1}{2}$をつけて、最終的にマージン最大化を行うということは次の二次計画問題を解くということに帰着します。
arg \min_{x,\omega}\frac{1}{2}||\omega||^2\\
\\subject \; to \;\; y_iL_1(x_i)\geq 1
以上がハードマージンにおけるマージン最大化の式化です。
線形データの分離
最後に線形分離できる2クラスのデータを対象としたサポートベクタマシンの適用例を紹介します。
以下が今回使用したコードです。
import numpy as np # ベクトル演算などに用いる
%matplotlib inline
# バックエンドをinlineに設定
import matplotlib.pyplot as plt # グラフの生成などに用いる
from sklearn import svm # サポートベクタマシンを扱うために用いる
from sklearn.datasets import make_classification # データセットを行うために用いる
# 散布図で独自のカラーマップを使用
from matplotlib.colors import ListedColormap # カラーマップをインポート
cm_bright = ListedColormap(['#FF0000', '#0000FF']) # カラーマップを定義
# データセットを行う
X, y = make_classification( n_samples=100, # サンプル数
n_features=2, # データセットの列数
n_informative=2, # 相関が強い特徴量の数
n_redundant=0, # 線形結合になる点の数(今回は線形データなので0)
n_classes=2, # クラス数
n_clusters_per_class=1, # 1クラス当たりのクラスター数
class_sep=2.0, # 値を大きくするとよりクラス間が分離
shift=None, # shiftの値をすべてのデータに追加
random_state=5) # 再現可能な乱数を生成
plt.scatter(X[:,0], X[:,1], c=y, cmap=cm_bright, edgecolors='k') # カラーマップの形式を指定
clf = svm.SVC(kernel='linear', C=1000) # 線形カーネルを使用してクラス分類
clf.fit(X, y) # データを学習
cbar = plt.scatter(X[:, 0], X[:, 1], s=30, c=y, cmap=cm_bright) # カラーマップの形式を指定
plt.colorbar(cbar) # カラーバーを表示
ax = plt.gca() # 現在のAxesオブジェクトを返す
xlim = ax.get_xlim() # x座標の表示範囲を指定
ylim = ax.get_ylim() # y座標の表示範囲を指定
xx = np.linspace(xlim[0], xlim[1], 30) # 等差数列を定義
yy = np.linspace(ylim[0], ylim[1], 30) # 等差数列を定義
YY, XX = np.meshgrid(yy, xx) # 定義された数列の各値の要素列から格子座標を作成
xy = np.vstack([XX.ravel(), YY.ravel()]).T # 縦方向に配列を結合
Z = clf.decision_function(xy).reshape(XX.shape) # Z座標を定義
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']) # マージンの境界線とクラス分類線を等高線に描画
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=200, c='w', edgecolors='k') # サポートベクタを白丸で描画
plt.show() # グラフを表示
testX=np.array([[1.0, -4.0], [1.0, -2.5]]) # クラス分類を行う新たなデータを定義
judge = clf.predict(testX) # データをクラス分類
judge # 判定
上記のコードは100個のサンプル数からなる線形データを線形カーネルを用いてサポートベクタマシンに適用しクラス分類線(超平面)を定義することにより、新たなデータがどのクラスに属するかを判定しています。
上記のコードの実行結果が
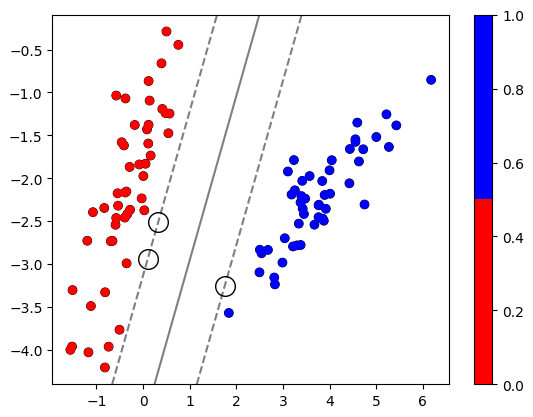
array([1, 0])
となり、1番目のデータはクラス1、2番目のデータはクラス0に属すると示されました。この結果は、図と照らし合わせることにより、正しいとわかります。
以上が線形分離できる2クラスのデータを対象としたサポートベクタマシンの適用例です。
まとめ
以上が、サポートベクタマシンによるハードマージンのマージン最大化の説明になります。
最後まで読んで頂きありがとうございました。引き続き私と一緒に研鑽していきましょう。
参考
橋本洋志,牧野浩二."データサイエンス教本 Pythonで学ぶ統計分析・パターン認識・深層学習・信号処理・時系列データ分析".オーム社,2018
0からはじめるPython ~パターン認識とは~
ハードマージン|マージン最大化により超平面を計算する方法