はじパタ5章の実行例をPythonで再現

はじめに

4章に引き続き、はじめてのパターン認識の実行例をPythonで再現していきます。今回は5章「k最近傍法（kNN法）」です。

ただし、ETL1手書き数字データベースを用いた実行例（実行例5.1, 実行例5.2 図5.9(a)）については、データをランダムにサンプリングしている箇所があるため、再現を断念しております。。。
記載したコードの動作環境は、numpy 1.16.2, pandas 0.24.2, scikit-learn 0.20.3 です。

実行例 5.2 最適な最近傍数 k を求める

k最近傍法（kNN法）は、あるサンプルの最近傍の鋳型（template）をk個とってきて、それらがもっとも多く所属するクラスにそのサンプルが所属するとする識別方法です。以下、コードです。

• 必要なライブラリの読み込み

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
from sklearn.preprocessing import StandardScaler

• k最近傍法の実装

class kNearestNeiborsClassifier:
    def __init__(self, k=5):
        self._k = k
        self._templates = None
        self._classes = None
    
    def fit(self, templates, classes):
        self._templates = templates
        self._classes = classes
    
    def predict(self, X):
        pred = np.zeros(len(X))
        for i in range(len(X)): # 可読性確保のためfor文で各サンプルについて処理
            distance = np.sum((X[i, :] - self._templates)**2, axis=1) # Xと鋳型のユークリッド距離を計算
            idx = np.argsort(distance)[:self._k] # Xとの距離が最も小さいk個の鋳型のインデックスを取得
            _, count = np.unique(self._classes[idx], return_counts=True) # k個の鋳型のうち、各クラスに所属する鋳型の数を算出
            cls = np.where(count == np.max(count))[0] # 所属する鋳型の数が最大になるクラスを特定
            if len(cls) == 1:
                pred[i] =  cls[0] # 所属する鋳型の数が最大になるクラスが1つなら、そのクラスを返す
            else:
                pred[i] =  np.nan # 所属する鋳型の数が最大になるクラスが複数なら、リジェクトとしてnp.nanを返す
        return pred
    
    def error_rate(self, y_true, y_pred):
        return np.sum(((y_true==1)&(y_pred==0))|((y_true==0)&(y_pred==1)))/len(y_pred) # リジェクトを除外して誤り率を算出
    
    def reject_rate(self, y_pred):
        return np.sum(np.isnan(y_pred))/len(y_pred) # リジェクト率

• ピマ・インディアンデータの読み込み

データはRdatasetsからお借りしています。

pima_train = pd.read_csv('https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/MASS/Pima.tr.csv')
pima_test = pd.read_csv('https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/MASS/Pima.te.csv')

• ホールドアウト法による誤り率を算出

# 学習用データ（X_train, Y_train）と検証用データ（X_test, Y_test）の準備
sc = StandardScaler()
X_train = sc.fit_transform(pima_train.drop(['Unnamed: 0', 'type'], axis=1))
Y_train = pima_train['type'].map({'Yes':1, 'No':0}).values

X_test = sc.transform(pima_test.drop(['Unnamed: 0', 'type'], axis=1))
Y_test = pima_test['type'].map({'Yes':1, 'No':0}).values

# k（奇数のみ）を変化させたときの誤り率を算出
hold_out_error_rate_list = np.empty((0,2), int)
for k in range(1, 120, 2):
    knn = kNearestNeiborsClassifier(k=k)
    knn.fit(X_train, Y_train)
    Y_pred = knn.predict(X_test)
    error_rate = knn.error_rate(y_true=Y_test, y_pred=Y_pred)
    hold_out_error_rate_list = np.append(hold_out_error_rate_list, np.array([[k, error_rate]]), axis=0)

• 一つ抜き法による誤り率を算出

# データの準備
pima = pd.concat([pima_train, pima_test])
sc = StandardScaler()
X = sc.fit_transform(pima.drop(['Unnamed: 0', 'type'], axis=1))
Y = pima['type'].map({'Yes':1, 'No':0}).values

# k（奇数のみ）を変化させたときの誤り率を算出
leave_one_out_error_rate_list = np.empty((0,2), int)
for k in range(1, 120, 2):
    error_list = []
    for i in range(len(X)):
        idx = np.ones(len(X), dtype=bool)
        idx[i] = False # インデックスiのサンプルは学習に使わない
        
        knn = kNearestNeiborsClassifier(k=k)
        knn.fit(X[idx], Y[idx]) # インデックスi以外のサンプルで学習
        
        Y_pred = knn.predict(X[i].reshape([1, -1]))
        error = knn.error_rate(y_true=Y[i], y_pred=Y_pred) # インデックスiのサンプルで検証
        error_list.append(error)
    error_rate = np.mean(error_list)
    leave_one_out_error_rate_list = np.append(leave_one_out_error_rate_list, np.array([[k, error_rate]]), axis=0)

• kの違いによる誤り率の変化 - 図5.9(b)

plt.scatter(hold_out_error_rate_list[:, 0], hold_out_error_rate_list[:, 1], label='hold out')
plt.scatter(leave_one_out_error_rate_list[:, 0], leave_one_out_error_rate_list[:, 1], label='leave one out')
plt.legend()
plt.xlabel('k')
plt.ylabel('error rate')
plt.show()

実行例 5.3 ベイズ誤りの推定

• 誤り率の算出

# k（奇数）を変化させたときのホールドアウト誤り率を算出
odd_error_rate_list = np.empty((0,2), int)
for k in range(1, 62, 2):
    knn = kNearestNeiborsClassifier(k=k)
    knn.fit(X_train, Y_train)
    Y_pred = knn.predict(X_test)
    error_rate = knn.error_rate(y_true=Y_test, y_pred=Y_pred)
    odd_error_rate_list = np.append(odd_error_rate_list, np.array([[k, error_rate]]), axis=0)

# k（偶数）を変化させたときのホールドアウト誤り率を算出  
even_error_rate_list = np.empty((0,2), int)
for k in range(2, 62, 2):
    knn = kNearestNeiborsClassifier(k=k)
    knn.fit(X_train, Y_train)
    Y_pred = knn.predict(X_test)
    error_rate = knn.error_rate(y_true=Y_test, y_pred=Y_pred)
    even_error_rate_list = np.append(even_error_rate_list, np.array([[k, error_rate]]), axis=0)

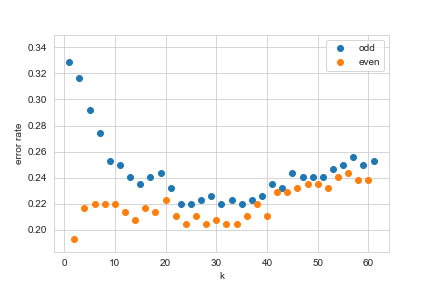
• 誤り率 - 図5.12(a)

plt.scatter(odd_error_rate_list[:, 0], odd_error_rate_list[:, 1], label='odd')
plt.scatter(even_error_rate_list[:, 0], even_error_rate_list[:, 1], label='even')
plt.legend()
plt.xlabel('k')
plt.ylabel('error rate')
plt.show()

• リジェクト率の算出

reject_rate_list = np.empty((0,2), int)
for k in range(2, 62, 2):
    knn = kNearestNeiborsClassifier(k=k)
    knn.fit(X_train, Y_train)
    Y_pred = knn.predict(X_test)
    reject_rate = knn.reject_rate(y_pred=Y_pred)
    reject_rate_list = np.append(reject_rate_list, np.array([[k, reject_rate]]), axis=0)

• リジェクト率 - 図5.12(b)

plt.scatter(reject_rate_list[:, 0], reject_rate_list[:, 1])
plt.xlabel('k')
plt.ylabel('reject rate')
plt.show()

おわりに

はじパタ5章の実行例について、Pythonで実行してみました。コードの誤りや、もっと効率の良い実装方法などありましたら、編集リクエストをして頂けると幸いです。