はじめに
統計的因果推論(以下、因果推論)は、マーケティングや医療分野において、施策や治療の効果をより正確に推定するためのフレームワークです。特に、
- 因果推論の使い時
- 傾向スコアによる逆確率重み付け法による施策効果推定方法
について簡単にまとめます。
最近は、因果推論に関する非常にわかりやすい入門書(効果検証入門~正しい比較のための因果推論/計量経済学の基礎)が出たので、因果推論も市民権を得てきた感じがします。
因果推論の使い時
因果推論の使い時は、ABテストはできないが、介入(マーケティング施策や治療)の効果をより正確に見積もりたいときです。
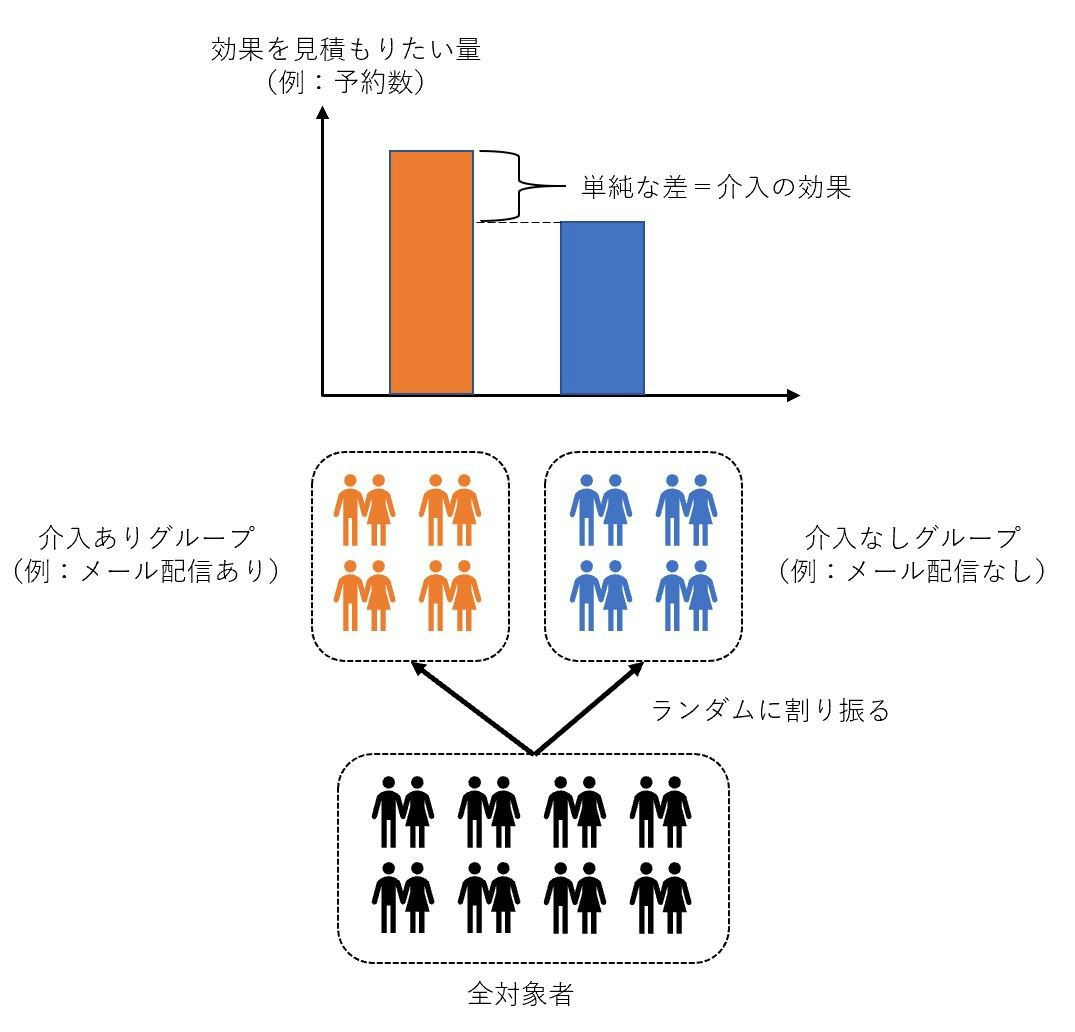
ABテスト(ランダム化比較試験(RCT: Randomized Controlled Trial)とも呼ぶ)は、対象者をランダムに2つのグループに割り振り、一方のグループには介入を実施し、もう一方のグループには介入を実施せず、両グループの結果を比較することで介入効果を見積もるものです。対象者をランダムに2つのグループに割り振り、介入有無以外は両グループで同質な集団をつくり出すことで、両グループの結果の単純な差分によって介入の平均的な効果を推定することができます。例えば、下図のように、ランダムに選択した半数のユーザーにはメールを配信し、残りの半数のユーザーにはメールを配信しないようにしたとき、それぞれのグループの平均予約数の差(=平均予約数の増分)が、メール配信施策による効果となります。
しかし、ABテストの実施にコストがかかるため、ランダムではないロジックで介入対象者が決まっている場合、上記の方法で介入効果を見積もることができません。
例えば、マーケティング施策の効果を見積もりたいものの、施策の実施対象者を半数に絞ることで、機会損失(売り上げの減少など)が発生する可能性が高い場合が該当します。また、治療の効果を見積もりたい場合など、治療の対象者をランダムに選定することが倫理に悖る場合も(広義的には)該当します。
ABテストを実施していないとき、介入ありグループの結果と介入なしグループの結果を単純に比較すると、介入以外の影響(バイアス)を除外できず、介入効果を過小(あるいは過大)に推定してしまう可能性があります。
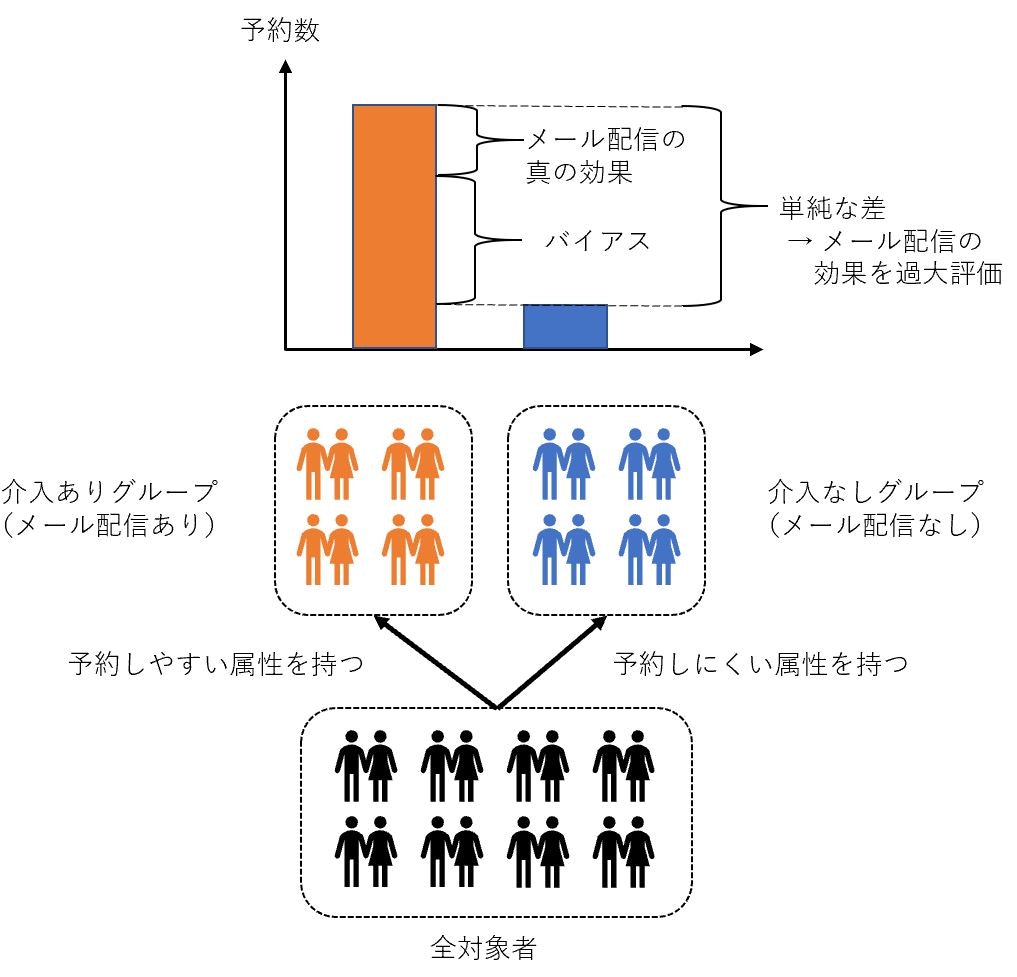
メール配信施策を例に説明します。機械学習などによって、ユーザーが予約するか否かを予測し、予測したスコアが高いユーザーにメールを配信する施策を実施しているとしましょう。このとき、メール配信対象となっているユーザーは、予約をしやすい属性を持っていると考えることができます。このとき、メール配信対象者の予約数と、非メール配信対象者の予約数の単純な差は、メール配信の効果と言えるでしょうか?答えはおそらくNOです。理由は、そもそも予約しやすい属性を持つユーザーにメールを配信しており、その分メール配信対象者の予約数は多いことが見込まれるため、メール配信以外の属性の影響で、メール配信の効果が過大に評価されるためです。
また、テレビCMの効果を見積もりたい場合など、対象者の意思で介入有無が決まる(CMを見るか見ないかは個人の自由であり、CMを放映する側が誰がCMを見るかを決めることはできない)場合も、介入有無がランダムに決まっていないため、介入ありグループと介入なしグループの単純比較では介入の効果を過大(あるいは過少)評価する可能性があります。
上記のような場合でも、介入の効果を推定するための方法論が、因果推論です。
傾向スコアを用いた逆確率重み付け法
ここでは、因果推論の手法の一つである、傾向スコアを用いた逆確率重み付け法(IPW: Inverse Probability Weighting)について説明します。
傾向スコアとは、対象者 $i$ が介入ありグループ(処置群)に属する確率であり、「対象者 $i$ の背景情報(属性)がこんな感じなので、対象者 $i$ が処置群へ属する確率(処置群への割り当てられやすさ)はこのくらい」という量を表します。式で書くと、対象者 $i$ の傾向スコア $e_i$ は、
e_i = P(Z_i =1| X=x_i)
です。$Z_i$ は、対象者 $i$ の群別を表す変数($Z_i=1$ なら介入ありグループ(処置群)に属する、$Z_i=0$ なら対照群(介入なしグループ)に属する)で、$x_i$ は対象者 $i$ の背景情報(共変量と呼びます)を表します。
ここまで、特に断りなく「平均的な」介入の効果を推定する、という説明をしてきました。その理由は、個人レベルでの介入効果を推定することはできない(因果推論の根本問題と呼びます)ためです。あるユーザーにメールを配信したときの予約数と、メールを配信しなかったときの予約数を同時に知ることはできないためです。そこで、介入有無以外は同質なグループをつくり、平均的な介入効果を推定するアプローチをとっています。
集計対象とする集団によって平均値が異なるように、平均的な介入効果も着目する集団に応じて異なります。基本的なものは、以下の3つです。
-
平均処置効果(ATE: Average Treatment Effect)
- 集団全体における、平均的な介入の効果
-
処置群における平均処置効果(ATT: Average Treatment effect on the Treated)
- 処置群(介入ありグループ)における、平均的な介入の効果
-
対照群における平均処置効果(ATU: Average Treatment effect on the Untreated)
- 対照群(介入なしグループ)における、平均的な介入の効果
それぞれを式で書くと、
ATE = E(Y_1) - E(Y_0) = \frac{\sum_{i=1}^{N} \frac{z_i}{e_i}y_i}{\sum_{j=1}^{N} \frac{z_j}{e_j}} - \frac{\sum_{i=1}^{N} \frac{1-z_i}{1-e_i}y_i}{\sum_{j=1}^{N} \frac{1-z_j}{1-e_j}}
ATT = E(Y_1 | Z=1) - E(Y_0 | Z=1) = \bar{y}_1 - \frac{\sum_{i=1}^{N} \frac{(1-z_i)e_i}{1-e_i}y_i}{\sum_{j=1}^{N} \frac{(1-z_j)e_j}{1-e_j}}
ATU = E(Y_1 | Z=0) - E(Y_0 | Z=0) = \frac{\sum_{i=1}^{N} \frac{z_i(1-e_i)}{e_i}y_i}{\sum_{j=1}^{N} \frac{z_j(1-e_j)}{e_j}} - \bar{y}_0
であり、$y_i$ は対象者 $i$ の結果変数(介入効果を推定する対象となる量。アウトカムとも呼ぶ。メール配信の例では予約数)を表します。
ATE, ATT, ATUいずれも、「着目する集団に介入したときの結果(第一項)」と「着目する集団に介入しないときの結果(第二項)」の差分です。
ATEは、集団全体に着目しています。第一項は処置群($z_i=1$の集団)を対象に、結果変数を傾向スコアの逆数で重み付けした平均値を計算しており、第二項は対照群($z_i=0$の集団)を対象に、結果変数を(1-傾向スコア)の逆数で重み付けした平均値を計算しています。傾向スコアを「対象者の処置群らしさ」、(1-傾向スコア)を「対象者の対照群らしさ」と解釈すれば、第一項では処置群を「処置群らしさ」で割ることでニュートラル(?)な集団とし、第二項では対照群を「対照群らしさ」で割ることでニュートラル(?)な集団としていると見做せます。つまり、介入有無に依存しない集団全体としての平均的な介入効果を推定しています。
ATTは、処置群に着目しており、「処置群における介入による結果変数の伸び(=処置群の結果変数の実績値と、処置群に仮に介入しなかった場合の結果変数の差分)」を表します。介入による直接的な利益を推定することができるため、介入の費用対効果を見積もるときに使われることが多いです。第一項 $\bar{y}_1$ は、処置群の結果変数の平均値(実績値)です。第二項は、対照群($z_i=0$の集団)を対象に、結果変数を 傾向スコア/(1-傾向スコア)で重み付けした平均値を計算しています。これは、対照群の結果変数を「対照群らしさ」で割り「処置群らしさ」を掛けることで、「処置群に仮に介入しなかった場合の結果変数」を推定していると解釈できます。
ATUは、対照群に着目しており、「対照群に仮に介入したときの結果変数の伸び(=対照群に仮に介入した場合の結果変数と、対照群の結果変数の実績値の差分)」を表します。現在は介入していない集団における介入効果を見積もることで、今後介入対象を拡大すべきかの判断に用いられることが多いです。第一項は、処置群($z_i=1$ の集団)を対象に、結果変数を(1-傾向スコア)/傾向スコアで重み付けした平均値を計算しています。これは、処置群の結果変数を「処置群らしさ」で割り「対照群らしさ」を掛けることで、「対照群に仮に介入した場合の結果変数」を推定していると解釈できます。第二項 $\bar{y}_0$ は、対照群の結果変数の平均値(実績値)です。
効果推定の実施手順
では、実際に介入の効果を推定してみましょう。ここでは、岩波DS vol.3のCM接触効果推定のデータを使い、CM接触がアプリ利用に与える効果の推定をpythonで実装します。ここでは、アプリ利用を促進するCMを放映することで、実際にアプリを利用する人の割合がどの程度増加したかを見積もります。CM施策による直接的な利益(=アプリを利用するユーザーの増加割合)を推定するため、ATTを推定します。推定手順は以下の通りです。
- 傾向スコア推定モデルを構築
- 傾向スコア推定モデルの推定精度を確認
- ATTを算出
以下、コードです。
- 必要なライブラリーをインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
import statsmodels.api as sm
from sklearn.calibration import calibration_curve
from sklearn.metrics import roc_auc_score
import itertools
import time
- 利用するデータの読み込み
「CMを見た/見ていない」の群別を表す変数を $Z$、TV視聴時間、性別や年齢などを共変量 $X$ とします。
data = pd.read_csv('./q_data_x.csv')
X = data[['TVwatch_day', 'age', 'sex', 'marry_dummy', 'child_dummy', 'inc', 'pmoney','area_kanto', 'area_tokai', 'area_keihanshin',
'job_dummy1', 'job_dummy2', 'job_dummy3', 'job_dummy4', 'job_dummy5', 'job_dummy6', 'job_dummy7',
'fam_str_dummy1', 'fam_str_dummy2', 'fam_str_dummy3', 'fam_str_dummy4']] # 共変量
Z = data['cm_dummy'] # 群別変数
- 傾向スコアの推定
共変量から各ユーザーの傾向スコアを推定します。ここでは、StatsModelsライブラリのLogit関数を使い、ロジスティック回帰により傾向スコア推定モデルを構築します。
exog = sm.add_constant(X) # 切片の追加
logit_model = sm.Logit(endog=Z, exog=exog) # ロジスティック回帰
logit_res = logit_model.fit()
- 傾向スコアの推定精度の確認
下記のコードで推定精度を見てみると、AUC=0.792でした。まずまずの推定精度といったところです。
ps = logit_res.predict(exog)
print('AUC = {:.3f}'.format(roc_auc_score(y_true=Z, y_score=ps)))
# 出力:=> AUC = 0.792
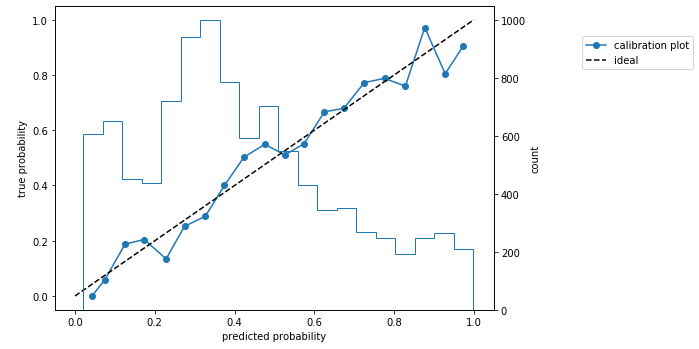
さらに下記のコードで、キャリブレーションプロットを描画してみます。キャリブレーションプロットがおおむね45度線に乗っているので、やはりまずまずの推定精度です。
_, ax1 = plt.subplots(figsize=(10, 5))
prob_true, prob_pred = calibration_curve(y_true=Z, y_prob=ps, n_bins=20)
ax1.plot(prob_pred, prob_true, marker='o', label='calibration plot')
ax1.plot([0,1], [0,1], linestyle='--', color='black', label='ideal')
ax1.legend(bbox_to_anchor=(1.2, 0.9), loc='upper left', borderaxespad=0)
ax1.set_xlabel('predicted probability')
ax1.set_ylabel('true probability')
ax2 = ax1.twinx()
ax2.hist(ps, bins=20, histtype='step', rwidth=0.9)
ax2.set_ylabel('count')
plt.tight_layout()
plt.show()
- ATTの推定
ATTを推定します。推定対象の結果変数は、アプリ利用ダミー変数(アプリ利用があれば1、なければ0をとる変数)です。下記のコードでATTを推定すると、CMによる効果は0.026(±0.013はブートストラップ法で算出した95%信頼区間)程度でとなりました。つまり、CM施策により、アプリを利用するユーザーの割合が2.6%程度増加することがわかりました。(岩波DS vol.3に記載の値と合致していることは確認済み)
Y = data['gamedummy'] # 結果変数(推定対象)
sample_size = len(data.loc[data['cm_dummy']==1])
ATT_list = []
for i in range(10000):
idx1 = pd.Series(data.loc[data['cm_dummy']==1, 'gamedummy'].index).sample(n=sample_size, replace=True, random_state=i)
idx0 = pd.Series(data.loc[data['cm_dummy']==0, 'gamedummy'].index).sample(n=sample_size, replace=True, random_state=i)
Z_tmp = np.r_[Z[idx1], Z[idx0]]
Y_tmp = np.r_[Y[idx1], Y[idx0]]
ps_tmp = np.r_[ps[idx1], ps[idx0]]
w01_tmp = (1-Z_tmp)*ps_tmp/(1-ps_tmp)
E1 = np.mean(Y_tmp[Z_tmp==1])
E0 = np.sum(Y_tmp * w01_tmp) / np.sum(w01_tmp)
ATT = E1 - E0
ATT_list.append(ATT)
print('ATT = {:.3f} ± {:.3f} (s.d.={:.3f})'.format(np.mean(ATT_list), np.std(ATT_list)*1.96, np.std(ATT_list)))
# 出力:=> ATT = 0.026 ± 0.013 (s.d.=0.006)
共変量の分布の確認
上記のコードでATTの推定ができましたが、これで正しく介入の効果は推定できたのか、もう一歩踏み込んでみます。
ATTの推定においては、第二項(処置群に仮に介入しなかった場合の結果変数の平均値)を傾向スコアを使って正しく推定することが重要です。そのためには、「対照群の結果変数の値」を「処置群に仮に介入しなかった場合の結果変数の値」にうまく調整できているか、つまり、傾向スコアを用いた調整により、対照群に属するユーザーの背景情報(共変量)が、処置群に属するユーザーの背景情報(共変量)と同質になっているかを確認することが必要です。傾向スコアの推定精度の確認はしていますが、共変量の分布が同質になっているかを優先的に確認すべきだと思います。確認の際は、結果変数と同様に、各共変量も傾向スコアで適切に重み付けします。
では、傾向スコアを用いた調整により、各群の共変量の分布が同質になるかを確認してみましょう。ここでは、標準化平均差(SMD: Standardized Mean Difference)という指標を使います。式で書くと、
SMD = \frac{\bar{x}_1 - \bar{x}_0}{\sigma_{pool}}
\sigma_{pool}^2 = \frac{(N_1-1)\sigma_1^2+(N_0-1)\sigma_0^2}{N_1+N_2-2}
です。処置群の共変量の平均値 $\bar{x}_1$ と対照群の共変量の平均値 $\bar{x}_0$ の差分を、プールした分散 $\sigma_{pool}^2$ の平方根をとった値で割ることで算出できます。$\sigma_1^2$ は処置群の共変量の分散、$\sigma_0^2$ は対照群の共変量の分散、$N_1$ は処置群のユーザー数、$N_0$ は対照群のユーザー数です。
SMDは、各群の平均値の差分が小さいとき、および分散が大きいときは、両群の共変量の分布に重なりが大きく、共変量の分布の差が小さいことを示す指標になっています。分布の差に関して判断するなら、コルモゴロフ=スミルノフ検定(KS検定)を実施する手もあるかと思いますが、これは「分布に統計的有意差がある」ことを示すための方法であるため、「分布が同質である(分布に差がない)」ことを示すために使うのは誤用だと思います。
では、各共変量の標準化平均差(SMD)を確認してみます。下記のコードでは、まず、SMDを計算する関数(standardized_mean_difference)と、傾向スコアを用いた調整前後のSMDを計算する関数(smd_on_the_treated)を定義しています。そして、各共変量について、傾向スコアを用いた調整前後のSMDをプロットしています。このプロットは、love plot と呼ばれます。
def standardized_mean_difference(X1, X0): # SMDを計算する関数
N1 = len(X1)
N0 = len(X0)
s_pool = ((N1-1)*np.var(X1)+(N0-1)*np.var(X0))/(N1+N0-2)
return (np.mean(X1)-np.mean(X0))/np.sqrt(s_pool)
def smd_on_the_treated(X, Z, ps): # 傾向スコアを用いた調整前後のSMDを計算する関数
X1 = X[Z==1]
X0 = X[Z==0]
ps0 = ps[Z==0]
X10 = X0*ps0/(1-ps0)
smd_before = standardized_mean_difference(X1, X0)
smd_after = standardized_mean_difference(X1, X10)
return smd_before, smd_after
# 各共変量について、傾向スコアを用いた調整前後のSMDを計算する
smd_list = []
for name in X.columns:
smd_before, smd_after = smd_on_the_treated(X=X[name], Z=Z, ps=ps)
smd_list.append([name, smd_before, smd_after])
smd_df = pd.DataFrame(smd_list, columns=['covariate', 'SMD(before)', 'SMD(after)'])
# 各共変量について、傾向スコアを用いた調整前後のSMDをプロットする(love plotを作成する)
plt.figure(figsize=(5, 10))
plt.scatter(smd_df['SMD(before)'], smd_df['covariate'], label='before')
plt.scatter(smd_df['SMD(after)'], smd_df['covariate'], label='after')
plt.vlines([0], ymin=-1, ymax=X.shape[1])
plt.legend()
plt.xlabel('standardized mean difference')
plt.ylabel('covariate')
plt.grid(True)
plt.show()
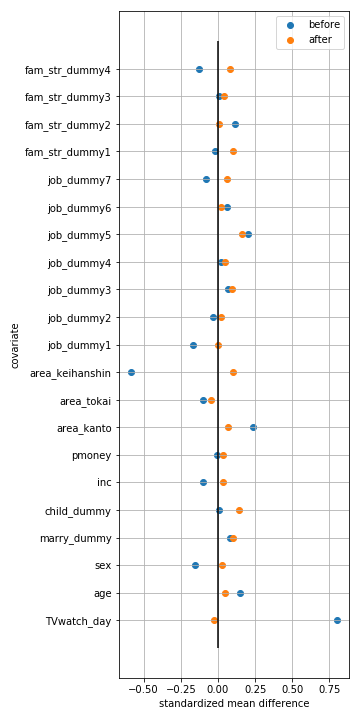
青点が傾向スコアを用いた調整前の共変量の群間のSMD、橙点が調整後の共変量の群間のSMDを示しています。これを見ると、TV視聴時間 (TVwatch_day)については、傾向スコアを用いた調整により、SMDが大きくが減少していることがわかります。ただし、子供の有無(child_dummy)など、傾向スコアを用いた調整により、むしろSMDが増加している共変量も見られます。
共変量の選択方法
上記のように共変量の分布が同質とならない原因として、傾向スコアの推定に利用するべき共変量が取り入れられておらず、隠れたバイアスが残ってしまっていることが考えられます。隠れたバイアスをなくすためには、「強く無視できる割り当て」条件が成り立つ必要があるのですが、この条件が成り立っているかを直接検証することは不可能であるため、間接的に条件が成り立つことをチェックし、共変量を選択することが多いようです。(「強く無視できる割り当て」条件の説明については専門書にゆずることとします。)
共変量選択の基本方針は、「結果変数と群別変数に関連のある共変量をなるべく多く入れる」です。選択手順は、
- 結果変数に関連のある変数を抽出
- 例:結果回数を目的変数、共変量候補の1つを説明変数として回帰分析を行い、疑似決定係数が上位のものを抽出
- 群別変数に関連のある変数を抽出
- 例:群別変数を目的変数、共変量候補の1つを説明変数として回帰分析を行い、疑似決定係数が上位のものを抽出
- 1., 2.で抽出した共変量の集合をマージ
- 結果変数に関連のある変数の上位が落ちないようにする
- 割り当てに関連のある変数よりも結果変数に関連のある変数を入れるほうが重要なため
- 割り当てに関連があるが結果変数に関連がない変数を入れると、結果変数に対する因果効果の推定分散が大きくなってしまう模様
- 共変量による割り当ての説明力の確認
- 3.までで選択した共変量で傾向スコア推定モデルを構築し、推定精度(AUCなど)を確認
- 共変量の分布の確認
- 標準化平均差(SMD)などの指標を使い、処置群・対照群で、傾向スコアによる調整後の共変量の分布が同質であるかを確認
です。1., 2.の例で回帰分析を行う、としていますが、ここはあくまで結果変数や群別変数に関連のある変数を抽出することが目的なので、この目的が達成されるなら、必ずしも回帰分析を行う必要はありません。4. では、傾向スコアの推定モデルの推定精度を確認していますが、この精度が高ければよいという話ではないことに注意してください。結果変数に対する因果効果の推定分散を低く抑えるため、群別変数より結果変数に関連が強い共変量を選択する必要があるためです。したがって、精度がいい機械学習アルゴリズムにより傾向スコアの推定精度を上げていく変数選択方法は方針として違うのではと思います。
おわりに
統計的因果推論、特に傾向スコアによる逆確率重み付け法による施策効果推定方法について、実施手順をPythonコードとともにまとめました。また、共変量の選択方法についても触れました。ただ、正しく効果推定ができているかの判断は難しいので、統計的因果推論のご利用は慎重に!と言わざるを得ません。
誤った記述などございましたらご指摘いただけると幸いです。