前書き
なぜ年末に第九なのか
ダイクストラ法とは
最短距離(経路)を計算するアルゴリズムです。
エッジのウェイトが0以上の時に利用できます。
具体的な手順は以下の通りです。
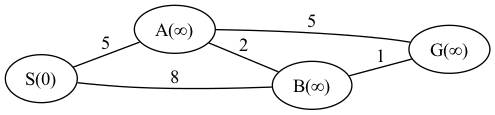
step 0. スタートのノードの距離を0、それ以外を無限大に設定する。
step 1. 未探索のノードで、距離が最小の点を見つける。
step 2. 1で見つけた距離が最小のノードを探索済みにする。このノードと接しているノードの距離を更新する。
step 3. ゴールのノードの距離が確定するまで、step 1 ~ 2を繰り返す。
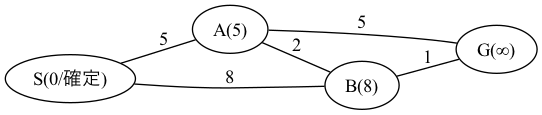
Aが距離最短のノードですので、Aの距離を確定してAの周りのノードの距離を計算します。
S -> A -> B の経路の方が S -> B の経路より短いので、Bの距離が7に更新されました。

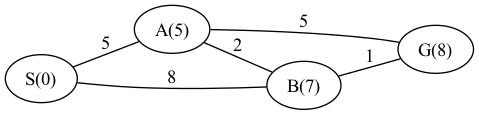
これを繰り返すと以下のようになり、ゴールまでの最短距離が8だとわかります。
実際、S -> A -> B -> G が距離8の最短経路になっています。
実装編
さっそく実装します。言語はD言語を使います。
ノードとエッジのクラスを定義する。
一応クラスを作っておきます。
まずは、ノードのクラス。
ノードの番号、距離と探索済みを表すフラグを持たせます。
step 1、2のことを考えて、ノードの距離を設定するメソッドと、ノードを探索済みにするメソッドを作っておきます。
class Node {
int nodeNumber;
int distance;
bool hasSearched;
this(int nodeNumber) {
this.nodeNumber = nodeNumber;
this.distance = int.max;
this.hasSearched = false;
}
void setDistance(int distance) {
if(distance < this.distance && !hasSearched) {
this.distance = distance;
}
}
void toSearched() {
this.hasSearched = true;
}
}
次はエッジのクラスです。
今回はエッジの一覧をEdge[][]として定義して、Edge[i]にはi番目のノードから出ているエッジ一覧を格納するようにして使うことにしましょう。
よって、行き先のノードの番号とウェイトをフィールドに持ちます。
class Edge {
int nodeTo;
int weight;
this(int nodeTo, int weight) {
this.nodeTo = nodeTo;
this.weight = weight;
}
}
標準入力
ノードの数$V$、エッジの数$E$、エッジの両端の点$v_i, u_i$とウェイト$w_i$を受け取ります。
形式は以下の通りです。
$V\ E$
$v_0\ u_0\ w_0$
$v_1\ u_1\ w_1$
$\vdots$
$v_E\ u_E\ w_E$
また、スタートは0番目のノード、ゴールは1番目のノードとします。
標準入力を受け取るコードは以下の通りです。
これで、$V$個のノードと$E$本のエッジの一覧を作成します。
int nodeAmount, edgeAmount;
readf("%d %d\n", &nodeAmount, &edgeAmount);
Node[] nodes = nodeAmount.iota.map!(i => new Node(i)).array;
Edge[][] edges = new Edge[][](nodeAmount);
edgeAmount.iota.each!( (i) {
auto input = readln.chomp.split.to!(int[]);
edges[input[0]] ~= new Edge(input[1], input[2]);
edges[input[1]] ~= new Edge(input[0], input[2]);
});
step 0
先ほど作ったNodeクラスのメソッドを使います。
nodes[0].setDistance(0);
アルゴリズム本体
こんな感じでループを回します。
while(!nodes[1].hasSearched) {
// 距離最小のノードを見つける
int currentNode = nodes.findMinNode;
// 距離最小のノードの距離を確定する
nodes[currentNode].toSearched;
// 新しいノードの周囲のノードの距離を計算する
int currentNodeDistance = nodes[currentNode].distance;
edges[currentNode].each!(it => nodes[it.nodeTo].setDistance(currentNodeDistance + it.weight));
}
findMinNode()はhasSearchedがfalseになっているノードの中から最短のものを計算します。
int findMinNode(Node[] nodes) {
int minNodeNumber = -1;
int minDistance = int.max;
nodes.each!( (it) {
if(!it.hasSearched && minDistance >= it.distance) {
minNodeNumber = it.nodeNumber;
minDistance = it.distance;
}
});
return minNodeNumber;
}
動かしてみる
コード全体
import std;
class Node {
int nodeNumber;
int distance;
bool hasSearched;
this(int nodeNumber) {
this.nodeNumber = nodeNumber;
this.distance = int.max;
this.hasSearched = false;
}
void setDistance(int distance) {
if(distance < this.distance && !hasSearched) {
this.distance = distance;
}
}
void toSearched() {
this.hasSearched = true;
}
}
class Edge {
int nodeTo;
int weight;
this(int nodeTo, int weight) {
this.nodeTo = nodeTo;
this.weight = weight;
}
}
void main() {
// 入力を受け取る
int nodeAmount, edgeAmount;
readf("%d %d\n", &nodeAmount, &edgeAmount);
Node[] nodes = nodeAmount.iota.map!(i => new Node(i)).array;
Edge[][] edges = new Edge[][](nodeAmount);
edgeAmount.iota.each!( (i) {
auto input = readln.chomp.split.to!(int[]);
edges[input[0]] ~= new Edge(input[1], input[2]);
edges[input[1]] ~= new Edge(input[0], input[2]);
});
// 0番目のノードはスタート地点
nodes[0].setDistance(0);
while(!nodes[1].hasSearched) {
// 距離最小のノードを見つける
int currentNode = nodes.findMinNode;
// 距離最小のノードの距離を確定する
nodes[currentNode].toSearched;
// 新しいノードの周囲のノードの距離を計算する
int currentNodeDistance = nodes[currentNode].distance;
edges[currentNode].each!(it => nodes[it.nodeTo].setDistance(currentNodeDistance + it.weight));
}
writeln(nodes[1].distance);
}
int findMinNode(Node[] nodes) {
int minNodeNumber = -1;
int minDistance = int.max;
nodes.each!( (it) {
if(!it.hasSearched && minDistance >= it.distance) {
minNodeNumber = it.nodeNumber;
minDistance = it.distance;
}
});
return minNodeNumber;
}
import std;
class Node {
int nodeNumber;
int distance;
bool hasSearched;
this(int nodeNumber) {
this.nodeNumber = nodeNumber;
this.distance = int.max;
this.hasSearched = false;
}
void setDistance(int distance) {
if(distance < this.distance && !hasSearched) {
this.distance = distance;
}
}
void toSearched() {
this.hasSearched = true;
}
}
class Edge {
int nodeTo;
int weight;
this(int nodeTo, int weight) {
this.nodeTo = nodeTo;
this.weight = weight;
}
}
void main() {
// 入力を受け取る
int nodeAmount, edgeAmount;
readf("%d %d\n", &nodeAmount, &edgeAmount);
Node[] nodes = nodeAmount.iota.map!(i => new Node(i)).array;
Edge[][] edges = new Edge[][](nodeAmount);
edgeAmount.iota.each!( (i) {
auto input = readln.chomp.split.to!(int[]);
edges[input[0]] ~= new Edge(input[1], input[2]);
edges[input[1]] ~= new Edge(input[0], input[2]);
});
// 0番目のノードはスタート地点
nodes[0].setDistance(0);
while(!nodes[1].hasSearched) {
// 距離最小のノードを見つける
int currentNode = nodes.findMinNode;
// 距離最小のノードの距離を確定する
nodes[currentNode].toSearched;
// 新しいノードの周囲のノードの距離を計算する
int currentNodeDistance = nodes[currentNode].distance;
edges[currentNode].each!(it => nodes[it.nodeTo].setDistance(currentNodeDistance + it.weight));
}
writeln(nodes[1].distance);
}
int findMinNode(Node[] nodes) {
int minNodeNumber = -1;
int minDistance = int.max;
nodes.each!( (it) {
if(!it.hasSearched && minDistance >= it.distance) {
minNodeNumber = it.nodeNumber;
minDistance = it.distance;
}
});
return minNodeNumber;
}
さっそくコンパイルして
dmd dijkstra.d
実行!
./dijkstra
- 先ほどの例
実行結果
❯ ./dijkstra
4 5
0 2 5
0 3 8
1 2 5
1 3 1
2 3 2
8 // <- 答え
テストケース1

おそらく 0 -> 3 -> 4 -> 1 の距離11が最短。
実行結果
❯ ./dijkstra
5 7
0 2 3
0 3 4
2 3 4
2 4 7
3 4 2
3 1 8
4 1 5
11 // <- 答え
テストケース2
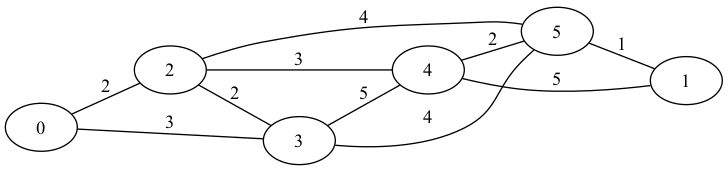
0 -> 2 -> 5 -> 1の距離7が最短。
実行結果
❯ ./dijkstra
6 10
0 2 2
0 3 3
2 3 2
2 4 3
3 4 5
2 5 4
3 5 4
4 5 2
4 1 5
5 1 1
7 // <- 答え
まとめ
なんとか年内に間に合いました。
ダジャレを成り立たせるために急いで書いたのでバグがあったら教えてください。
距離最短のノードの検索方法を変えるともう少し計算量のオーダーが改善されるらしい。
今後も勉強を兼ねていろんなアルゴリズムを実装していけたらと思っています。
参考
-
- さらにPriorityQueを使う方法や、最短経路を取得する方法などが解説されています。
-
スペシャルサンクス: 弟
- テストケースの作成を手伝ってもらいました。