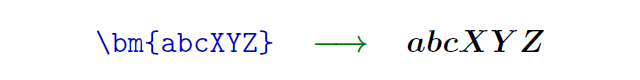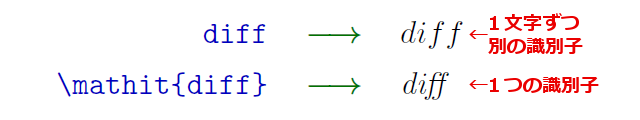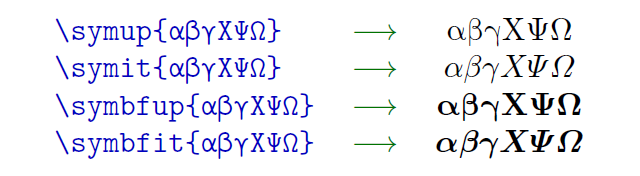徹底解説！ unicode-mathパッケージでココが変わる

LuaTeXの1.0版が2016年にリリースされてから6年以上が経ち、日本でもかなりLuaLaTeXを常用する人が増えてきました。それに伴い、“LuaLaTeX上の究極の数式フォントパッケージ” であるunicode-mathパッケージを紹介する記事も現れ始めています。本記事では「unicode-mathにより従来と書き方が変わる点」というテーマについて解説します。

前提知識

• フツーのLaTeXの数式の書き方に関するフツーの知識。

導入の話

unicode-mathパッケージは​「fontspecの数式フォント版」​に相当するもので、「数式フォントをUnicodeのものにする」とともに「簡単に任意のOpenType数式フォントを指定する」という機能を提供します。従来のLaTeXにおける「数式フォントごとに別々のパッケージが存在する」という状況を脱して、統一的に数式フォントを扱うことを可能にしています。

このように便利なunicode-mathパッケージですが、注意点もあります。unicode-mathにおける数式書体の扱いはUnicodeの数式書体の考えを取り入れていて、従来より多機能になっています。それだけならいいのですが、問題は、それに伴って「従来の書き方と比べると正しい書き方が変わる」点が生じているということです。具体的には\mathrmなどの「数式のフォント選択（太字・斜体など¹）の命令」の体系についてunicode-mathでは大きな変更があります。

本記事では一般のLaTeXユーザ向けに、unicode-mathにおける​「数式フォント選択の命令」​について、従来の書き方から変わる点に話を絞って解説します。

つまり、本記事では「unicode-math特有の便利な機能」については敢えて扱わないことにします。便利な機能を紹介する記事を書こうとする人は今後増えていくだろうと期待しているからです。

実際には「従来の書き方を続けても実害がでない」ように互換性が配慮されています。だからといって漫然と従来の書き方を続けていると、将来unicode-mathが普及したときには、もしかしたら​「未だに \rm や\bf を使っている人たちと同類」​の立場に追いやられるかもしれません。

従来のLaTeXの数式フォントの話

unicode-mathの話の前に、まずは従来の標準（LaTeXカーネルおよびamsfontsの範囲）における数式フォントの扱いについて復習しておきましょう。

従来の数式フォント選択命令

テキスト（非数式）と数式では「書体の違い」が意味するものが異なるため、LaTeXではテキストと数式でフォント選択命令を使い分けられています。数式用のフォント選択命令²は\mathXXという形の名前をもち、文字（数字や英字）にのみ作用するのでした。標準の範囲では次の数式フォント命令が用意されています。

• \mathrm{«文字»}：立体（正確には“セリフ・中字・立体”³）
• \mathit{«文字»}：斜体⁴（“セリフ・中字・斜体”）
• \mathbf{«文字»}：太字立体（“セリフ・太字・立体”）
• \mathsf{«文字»}：サンセリフ立体（“サンセリフ・中字・立体”）
• \mathtt{«文字»}：等幅立体（“等幅・中字・立体”）
• \mathcal{«文字»}：筆記体
• \mathbb{«文字»}：黒板太字
• \mathfrak{«文字»}：ドイツ文字

数式用の書体として日本では太字の斜体もよく使われますが、標準の数式フォント命令の範囲ではこれはサポートされていないので、例えばbmパッケージの\bm命令のような「別系統の命令」を利用する必要がありました。

“数式イタリック”

LaTeXの数式フォントについて注意すべき点は「“数式イタリック” と “普通のイタリック” の区別があること」です。数式フォント命令（\mathXX）を指定しない状態で英字を書くとそれは斜体（イタリック）になるのですが、その字体はいわゆる “数式イタリック” であり、「文字が1文字だけで識別子を表す」場合にのみ用いることが想定されている（その用途で適切に見えるように字形や字間がデザインされている）のでした。複数文字からなる斜体の識別子を書くときには\mathit命令を指定して “普通のイタリック” を使う必要があります。

しかし従来のLaTeXでは “1文字” と “複数文字” で区別をつけるのは斜体だけで、その他の書体、例えば立体については “1文字” でも “複数文字” でも区別せずに\mathrmを使うことになっていました。

unicode-mathの数式フォントの話

1文字用の数式フォント命令

unicode-mathパッケージでは、先述の「“1文字” と “複数文字” の区別」をより広範の書体について行うように設計されています。次の表に示すように、従来の\mathXXという名前の数式フォント命令は “複数文字用” のものと規定されていて、新たに\symXXという名前の命令が “1文字用” の数式フォント命令として用意されます。

フォントの種類	1文字用命令	複数文字用命令
立体（セリフ・中字・立体）	\symup	\mathrm
斜体（セリフ・中字・斜体）	\symit	\mathit
太字立体（セリフ・太字・立体）	\symbf	\mathbf
太字斜体（セリフ・太字・斜体）	\symbfit	―
サンセリフ立体（サンセリフ・中字・立体）	\symsf	\mathsf
等幅立体（等幅・中字・立体）	\symtt	\mathtt
筆記体	\symscr	―※1
黒板太字	\symbb	―※1
ドイツ文字	\symfrak	―※1

(※1) 筆記体・黒板太字・ドイツ文字は「複数文字の識別子を書くことが想定されていない」ため複数文字用のフォント選択命令は用意されていません⁵。

また、従来のLaTeXではサポートされていなかった「太字の斜体」についても、\symbfitという数式フォント命令が用意されている⁶ので、「太字斜体だけ他の書体と扱いが異なる」という不自然な状況も解消されます。unicode-mathの既定の状態⁷での出力例を示します。

よく見ると、斜体（\symitや\symbfit）を指定したときも数字は立体で出力されています。これは数式で斜体の数字が用いられることは想定されていない⁸からです。

また、従来の\mathcalや\mathbbは英字大文字にのみ対応していたのに対して、unicode-mathの\symscrは英字小文字にも対応⁹していて、また\symbbは英字大文字小文字に加えて数字にも対応しています。これらの文字のために別のパッケージを読み込む必要はありません。

従来のLaTeXでは数式フォント命令を指定しない場合の書体は特別な “数式イタリック” でしたが、unicode-mathでは “数式イタリック” に相当するもの（1文字用の斜体）が\symitなので、英字¹⁰については既定の書体は\symitと同等になります。つまり普通は\symitを用いる必要はありません。

ギリシャ文字の話もしてみる

従来の標準のLaTeXの範囲ではギリシャ文字の扱いは英字（ラテン文字）と色々な点で異なっていて厄介で、さらにギリシャ小文字については標準の範囲では斜体のみに限られていました。unicode-mathではギリシャ文字（大文字・小文字ともに）についても普通に数式フォント命令で書体を変えることができます。

• \symup{α}・\symup{\alpha}・\symup{Ω}・\symup{\Omega} → 立体
• \symit{α}・\symit{\alpha}・\symit{Ω}・\symit{\Omega} → 斜体

ただし太字については注意が必要です。先ほどの表では「太字」の数式フォント命令は\symbfでしたが、これを使うと（従来の習慣を踏襲するため）ギリシャ小文字が「太字斜体」になってしまいます。そこで代わりに明示的に「太字の立体」を指定する命令である\symbfupを使う必要があります。まとめると、ギリシャ文字に使うべき数式フォント命令は以下のようになります（これ以外の書体はサポートされない¹¹）。

フォントの種類	1文字用命令
立体（セリフ・中字・立体）	\symup
斜体（セリフ・中字・斜体）	\symit
太字立体（セリフ・太字・立体）	\symbfup
太字斜体（セリフ・太字・斜体）	\symbfit

unicode-mathの既定の状態でのギリシャ文字の出力例を示します。

補足：立体と斜体の振り分けの話

先ほど「\symbfではギリシャ小文字だけ斜体になる」という話をしましたが、これを聞いて「なぜ1つの命令が1つの書体に単純に対応していないのか」とモヤモヤした人もいるでしょう。そこで補足として「symbfの仕様がそうなっている理由」について解説します。

そもそも従来のLaTeXでは数式フォント命令を使わない状態（これを “既定状態” と呼ぶことにします）の文字¹²の入力は、文字種によって立体と斜体に “振り分け” られていました。具体的には、ギリシャ大文字だけ立体、それ以外は斜体になります。

この規則はunicode-mathにも踏襲されていて、unicode-mathの用語を使うと次のように言い表せます。

• 既定状態の文字は文字種によって、\symup（セリフ・中字・立体）と\symit（セリフ・中字・斜体）の何れかに振り分けられる。

そしてunicode-mathではこのような「文字種により立体と斜体に振り分ける」入力を既定状態（セリフ・中字）以外にも拡張しています。その1つが\symbf（セリフ・太字）であり、いわば\symbfは既定状態に対する “太字版” に相当するといえます。つまり\symbfの規則は次の通りです。

• \symbfの文字は文字種によって、\symbfup（セリフ・太字・立体）と\symbfit（セリフ・太字・斜体）の何れかに振り分けられる。

まとめると、unicode-mathの “1文字用” の数式フォント命令は​「特定の書体に対応するもの」​と​「立体・斜体を振り分けるもの」​の2種類があります。unicode-mathの既定設定¹³では具体的な振り分けの規則は以下のようになっています。

	ラテン	ギリシャ大	ギリシャ小
“既定状態”の振り分け	\symit	\symup	\symit
\symbfの振り分け	\symbfup	\symbfup	\symbfit

これを見ると、ラテン文字は従来の挙動（既定と\mathbf）と同じになりますが、一方でギリシャ文字の挙動は馴染みがない人が多いでしょう。なので私は「ラテン文字は振り分けを使う、ギリシャ文字は使わない」という方針を推奨したのでした。

ほとんどの人は「数式モードでaと書けば斜体、2と書けば立体になる」ことを期待するはずで、その意味で「立体と斜体の振り分け」は重要な機能です。しかし、unicode-mathの既定の「振り分けの規則」は従来のLaTeXとの互換を重視していて無駄に複雑になっている点もあり、これを不便だと感じる人もいるでしょう。

unicode-mathではオプションで「振り分けの規則」を変更することができます。以下の記事では「常に斜体を優先する」設定について解説しています。

• 重点解説！ unicode-mathをもっと幸せに使う話

既定設定が不便だと感じたら、こちらの設定を試してみるのもいいでしょう。

付録：最後に全書体の話

本編では「従来のLaTeXでサポートされる書体」に対象を限って説明していたが、最後に付録として、unicode-mathでサポートされる1文字用の数式書体全ての一覧を載せておく。

書体	命令	ラテン	ギリシャ	数字
セリフ・中字・立体	\symup	✔	✔	✔
セリフ・中字・斜体	\symit	✔	✔
セリフ・太字・立体	\symbfup	✔	✔	✔
セリフ・太字・斜体	\symbfit	✔	✔
サンセリフ・中字・立体	\symsfup	✔		✔
サンセリフ・中字・斜体	\symsfit	✔
サンセリフ・太字・立体	\symbfsfup	✔	✔	✔
サンセリフ・太字・斜体	\symbfsfit	✔	✔
等幅	\symtt	✔		✔
筆記体・中字	\symscr	✔
筆記体・太字	\symbfscr	✔
黒板太字・立体	\symbb	✔		✔
黒板太字・斜体	\symbbit	※1
ドイツ文字・中字	\symfrak	✔
ドイツ文字・太字	\symbffrak	✔

※ 「ラテン」「ギリシャ」「数字」の欄は「その書体が使えるか」を示す。
※1 一部のラテン文字のみ使用可能。

立体・斜体の振り分けをする命令の一覧。

書体	命令 →	ラテン	ギリシャ大	ギリシャ小
セリフ・中字	既定 →	\symit	\symup	\symit
セリフ・太字	\symbf →	\symbfup	\symbfup	\symbfit
サンセリフ・中字	\symsf →	\symsfup	―	―
サンセリフ・太字	\symbfsf →	\symbfsfup	\symbfsfup	\symbfsfup

まとめ

ここまで読めばもうunicode-mathしぐさはバッチリです！ これからドンドンunicode-mathの便利な機能を習得していきましょう！

1. この記事でいう「フォント」とは「Times」のような具体的な書体種別ではなく「太字」「斜体」などの抽象的な区別を指します。「斜体」にどの具体書体を充てるかといった設定の機構はこの記事では扱いません。 ↩

2. 「数式用のフォント選択命令」を表す正式な用語は「数式英字命令（math alphabet command）」のようです。 ↩

3. テキストのフォントには「ファミリ」「シリーズ」「シェープ」という3つの属性に分けて管理されていて、テキストのフォント選択命令は1つの属性のみを変更する（例えば\textbfならシリーズを「太字」に変える）仕組になっています。これに対して、数式のフォントは（少なくともテキストフォントにあるような）属性をもっていません。従って、数式のフォント選択命令は常に特定の1つの書体を指定する（例えば\mathbfなら「セリフ・太字・立体」に変える）役割をもっています。 ↩

4. 数式では真の斜体（oblique）を用いることはないので、この記事では「斜体」を「イタリック体」と同義として扱うことにします。 ↩

5. 一応、互換性のために\mathcal・\mathbb・\mathfrak命令が\symscr・\symbb・\symfrakの別名として定義されていますが、これらは「名前が “\math…” なのに実態は1文字用命令である」という紛らわしい状況になっているので使用は推奨されません。 ↩

6. なお滅多に使われないと思いますが（一応従来のLaTeXの範囲に含まれるので補足しておくと）、「太字の筆記体」に対する\symbfscr、「太字のドイツ文字」に対する\symbffrakという数式フォント命令も用意されています。 ↩

7. unicode-mathの既定状態では具体書体としてOpenType版の「Latin Modern Math」が使われます。このフォントは従来のComputer Modernの数式フォントの書体を継承するものです。 ↩

8. もちろん「複数文字の斜体の識別子に数字が含まれる」場合にはその数字も斜体になるべきですから、“複数文字用” の\mathitでは数字も斜体になります。 ↩

9. ただし既定の具体書体である「Latin Modern Math」は英字小文字の筆記体の字形をもっていないようで、そのため例出の画像では既定の（斜体の）字形が代替出力されています。英字小文字の筆記体の字形をもつ数式フォントに切り替えるとちゃんとその字形が出力されます。 ↩

10. 数字の既定の書体は\symupと同等になります。先述の通り、数字は決して斜体にはなりません。 ↩

11. これは嘘で、実際には「サンセリフ太字の立体・斜体」もサポートされています。不思議なことにサンセリフのギリシャ文字は太字だけがサポートされていて中字が入っていません。これはUnicodeの数式書体がそのように定められているからなのですが、そもそもUnicodeの規定がなぜこうなっているかが全くの謎です。 ↩

12. unicode-mathでは数字は常に立体になるので、ここでは数字は含めずに英字（ラテン文字）とギリシャ文字だけを「文字」として扱うことにします。 ↩

13. 振り分けの規則は複数のパターンが用意されていて、unicode-mathパッケージに対する設定でパターンを選択できます。 ↩