Cairoを使う：（その9）剪断変形・鏡像反転と変換行列

剪断変形・鏡像反転

剪断変形とは、座標軸を斜交させる変形です。次の図は、前回用いたdraw_shape()関数を用いて剪断変形を施した例です。

これを出力したdraw()関数を次に示します。

void draw(cairo_t *c, int width, int height)
{
  cairo_matrix_t matrix;

  /* background */
  cairo_set_source_rgb( c, 1, 1, 1 );
  cairo_rectangle( c, 0, 0, width, height );
  cairo_fill( c );
  /* transform test */
  cairo_translate( c, width/3, height/3 );
  draw_shape( c, width, height );
  cairo_matrix_init( &matrix, 2, 0.5, 0, 1, 0, 0 );
  cairo_transform( c, &matrix );
  draw_shape( c, width, height );
}

cairo_matrix_t型は、剪断変形を含めた座標変換を行うための行列（定数群）です。少しだけ数学的な背景を説明すると、Cairoで扱っている座標変換とは具体的には次のような計算です。

x'=ax+cy+x_0 \\
y'=bx+dy+y_0

座標$(x,y)$を、6つの定数$a, b, c, d, x_0, y_0$を用いて上式のように別の座標$(x',y')$に変更するわけです。これらの定数をcairo_matrix_t型にセットするのがcairo_matrix_init( matrix, a, b, c, d, x0, y0 )関数です。cairo_transform()関数でmatrixをコンテクストに与えた後に描画関数（例えばcairo_rectangle()やcairo_line_to()）で指定した座標$(x,y)$は、全て上式に従って$(x',y')$に変換されます。

上式の意味を解釈するために、次のように書き直してみます。

\left[\begin{array}{c}
x' \\ y'
\end{array}\right]
=
\left[\begin{array}{c}
a \\ b
\end{array}\right]
x
+\left[\begin{array}{c}
c \\ d
\end{array}\right]
y
+
\left[\begin{array}{c}
x_0 \\ y_0
\end{array}\right]

これを、「新しい座標系$x'$-$y'$では元の座標の$x$の値を$[a,b]$方向に、$y$の値を$[c,d]$方向にそれぞれ延ばした後で$(x_0,y_0)$平行移動する」と解釈します。
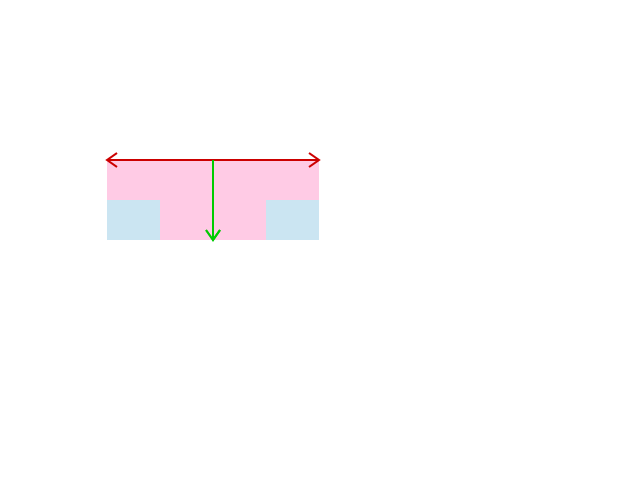
上の描画例では$[a,b]=[2,0.5]$, $[c,d]=[0,1]$, $[x_0,y_0]=[0,0]$としているので、$x$軸を表す赤い矢印が右斜め下に伸び、$y$軸を表す緑の矢印は（長さと方向は）変化していません。

剪断変形の分かりやすい応用の一つは、疑似的な立体描画だろうと思います。次のコードを試してみて下さい。

# include <stdio.h>
# include <X11/Xutil.h>
# include <X11/Xlib.h>
# include <X11/keysym.h>
# include <X11/XKBlib.h>
# include <cairo/cairo.h>
# include <cairo/cairo-xlib.h>

void draw_rect(cairo_t *c, cairo_pattern_t *p, int imgwidth, int imgheight)
{
  cairo_rectangle( c, 0, 0, imgwidth, imgheight );
  cairo_set_source( c, p );
  cairo_fill_preserve( c );
  cairo_set_source_rgb( c, 0, 0, 0 );
  cairo_set_line_width( c, 5 );
  cairo_set_line_join( c, CAIRO_LINE_JOIN_ROUND );
  cairo_stroke( c );
}

void draw_shear_rect(cairo_t *c, cairo_pattern_t *p, int imgwidth, int imgheight, double x0, double y0, double x1, double y1, double x2, double y2)
{
  cairo_matrix_t matrix;

  cairo_save( c );
  cairo_translate( c, x0, y0 );
  cairo_matrix_init( &matrix, (x1-x0)/imgwidth, (y1-y0)/imgheight, (x2-x0)/imgwidth, (y2-y0)/imgheight, 0, 0 );
  cairo_transform( c, &matrix );
  draw_rect( c, p, imgwidth, imgheight );
  cairo_restore( c );
}

void draw(cairo_t *c, int width, int height, cairo_pattern_t *p, int imgwidth, int imgheight)
{
  /* background */
  cairo_set_source_rgb( c, 1, 1, 1 );
  cairo_rectangle( c, 0, 0, width, height );
  cairo_fill( c );
  /* image rectangle */
  draw_shear_rect( c, p, imgwidth, imgheight, 100, 100, 300, 50, 320, 150 );
  draw_shear_rect( c, p, imgwidth, imgheight, 100, 100, 320, 150, 100, 350 );
  draw_shear_rect( c, p, imgwidth, imgheight, 320, 150, 520, 100, 320, 400 );
}

int main(int argc, char** argv)
{
  Display *display;
  XEvent event;
  Window win;
  cairo_surface_t *cs = NULL;
  cairo_surface_t *s;
  cairo_pattern_t *p;
  cairo_t *c = NULL;
  int width = 640, height = 480;
  int imgwidth, imgheight;
  int quit_flag = 0;

  display = XOpenDisplay( NULL );
  win = XCreateSimpleWindow( display, RootWindow( display, DefaultScreen(display) ),
    0, 0, width, height, 0,
    WhitePixel( display, DefaultScreen(display) ),
    BlackPixel( display, DefaultScreen(display) ) );
  XMapWindow( display, win );
  XSelectInput( display, win, ExposureMask | KeyPressMask | KeyReleaseMask );

  s = cairo_image_surface_create_from_png( "splash.png" );
  p = cairo_pattern_create_for_surface ( s );
  imgwidth = cairo_image_surface_get_width( s );
  imgheight = cairo_image_surface_get_height( s );

  while( quit_flag != 1 ){
    XNextEvent( display, &event );
    switch( event.type ){
    case Expose:
    case ConfigureNotify:
      if( event.xexpose.count >= 1 ) break;
      cairo_destroy( c );
      cairo_surface_destroy( cs );
      width = event.xexpose.width;
      height = event.xexpose.height;
      cs = cairo_xlib_surface_create( display, win, DefaultVisual(display,0), width, height );
      c = cairo_create( cs );
      draw( c, width, height, p, imgwidth, imgheight );
      break;
    case KeyPress:
      switch( XkbKeycodeToKeysym( display, event.xkey.keycode, 0, 0 ) ){
      case XK_q: case XK_Q: case XK_Escape: return -1;
      }
      break;
    default: ;
    }
  }
  cairo_destroy( c );
  cairo_surface_destroy( cs );

  cairo_pattern_destroy( p );
  cairo_surface_destroy( s );

  XDestroyWindow( display, win );
  XCloseDisplay( display );
  return 0;
}

ちょっと長くて済みません。draw_rect()は指定されたPNG画像をパターンとして長方形内に描画するだけの関数で、その次のdraw_shear_rect( c, p, imgwidth, imgheight, x0, y0, x1, y1, x2, y2 )で、上記長方形を(x0,y0)から(x1,y1)および(x2,y2)に伸びる二辺にフィットする平行四辺形に剪断変形しています。PNG画像のサイズimgwidth x imgheightは、main()関数の中でcairo_image_surface_get_width()およびcairo_image_surface_get_height()を呼ぶことで取得していることにも注意して下さい。出力は次のようになります。

剪断変形に比べれば鏡像反転は分かりやすいです。例えば$[a,b]=[-1,0]$, $[c,d]=[0,1]$とすると
x軸のみが反転する、つまりy軸に関する鏡像反転になります。前のコードに戻って、行列を与える部分を

  cairo_matrix_init( &matrix,-1, 0, 0, 1, 0, 0 );

としてみましょう。出力は次のようになります。

座標変換の数学的説明

前回から上記までの説明で、Cairoで行える座標変換は全てカバーされます。ここからはもう少し突っ込んだ説明になります。
改めて次の式を考えましょう。

\left[\begin{array}{c}
x' \\ y'
\end{array}\right]
=
\left[\begin{array}{c}
a \\ b
\end{array}\right]
x
+\left[\begin{array}{c}
c \\ d
\end{array}\right]
y
+
\left[\begin{array}{c}
x_0 \\ y_0
\end{array}\right]

$[a,b]=[1,0]$, $[c,d]=[0,1]$ならば、上式は$(x,y)$を$(x_0,y_0)$平行移動するだけの変換です。前回説明したcairo_translate()はまさにこれらの値を与える関数です。
また$b$と$c$がともに0ならば、上式は$(x,y)$を$(x_0,y_0)$平行移動した後に、$x$を$a$倍、$y$を$d$倍する変換、つまり拡大・縮小です。前回説明したcairo_scale()ではこの操作を行っています。
さらに、上の式が次のような特別な値を持っているとしましょう。

\left[\begin{array}{c}
x' \\ y'
\end{array}\right]
=
\left[\begin{array}{c}
\cos\theta \\ \sin\theta
\end{array}\right]
x
+\left[\begin{array}{c}
-\sin\theta \\ \cos\theta
\end{array}\right]
y
+
\left[\begin{array}{c}
x_0 \\ y_0
\end{array}\right]

$[\cos\theta,\sin\theta]$は$x$軸が反時計回りに$\theta$傾いた方向、$[-\sin\theta,\cos\theta]$は$y$軸が反時計回りに$\theta$傾いた方向をそれぞれ表しますので、これは$(x,y)$を$(x_0,y_0)$平行移動した後に反時計回りに$\theta$回転する変換を表しています。cairo_rotate()はこのような変換を行っています。
つまり、前回説明した平行移動、回転、拡大・縮小も全て行列で表現できるということです。そして、これらに当てはまらない$a, b, c, d$が今回説明した剪断変形と鏡像反転の要素を持つことになります。

座標変換行列の取得とリセット

Cairoコンテクスト（正確にはコンテクストと関連付けられたサーフェス）は、内部に座標変換行列を一つ持ちます（同時に逆変換行列も一つ持つのですが、これはあまり気にしなくて構いません）。
cairo_transform()は、与えられたcairo_matrix_t型インスタンスを今の座標変換に合成する関数です。cairo_translate()もcairo_rotate()もcairo_scale()も内部計算としては上述の通り6つの定数を使った変換ですので、cairo_transform()と同様の操作を行っています。
cairo_get_matrix()関数を用いれば、現在の変換行列を取得できます。あまり面白くないコードですが、次を試してみて下さい。

# include <cairo/cairo.h>
# include <stdio.h>

void matrix_print(cairo_t *c)
{
  cairo_matrix_t matrix;

  cairo_get_matrix( c, &matrix );
  printf( "a=%g, c=%g, x0=%g\n",   matrix.xx, matrix.xy, matrix.x0 );
  printf( "b=%g, d=%g, y0=%g\n\n", matrix.yx, matrix.yy, matrix.y0 );
}

void matrix_test(cairo_t *c)
{
  /* initial matrix */
  matrix_print( c );
  /* translate */
  cairo_translate( c, 10, 20 );
  matrix_print( c );
  /* scale */
  cairo_scale( c, 2, 3 );
  matrix_print( c );
  /* translate */
  cairo_translate( c, 10, 20 );
  matrix_print( c );
}

int main(int argc, char** argv)
{
  cairo_surface_t *cs;
  cairo_t *c;
  int width = 640, height = 480;

  cs = cairo_image_surface_create( CAIRO_FORMAT_ARGB32, width, height );
  c = cairo_create( cs );
  matrix_test( c );
  cairo_destroy( c );
  cairo_surface_destroy( cs );
  return 0;
}

これは描画は行わず、自前関数matrix_print()を使って現在の座標変換行列の中身を出力するだけのプログラムです。結果は次のようになります。

a=1, c=0, x0=0
b=0, d=1, y0=0

a=1, c=0, x0=10
b=0, d=1, y0=20

a=2, c=0, x0=10
b=0, d=3, y0=20

a=2, c=0, x0=30
b=0, d=3, y0=80

初期状態での座標変換が「何もしない」つまり$(x,y)$をそのまま出力するものになっていることに注意して下さい。
後は理解通りの値になっています。

上述のような段階的合成プロセスをすっとばして、ダイレクトに行列を指定してしまう関数がcairo_set_matrix()です。例えばmatrix_test()関数の最後に次を追記してみて下さい。

  /* direct set */
  cairo_matrix_init( &matrix, 1, 2, 3, 4, 5, 6 );
  cairo_set_matrix( c, &matrix );
  matrix_print( c );

実行すると、先程と同じ表示に続いて次が出力されるはずです。

a=1, c=3, x0=5
b=2, d=4, y0=6

また、強制的に初期状態の座標変換（つまり「何もしない」変換）に戻すにはcairo_identity_matrix()を呼びます。matrix_test()の最後に次を追記してみて下さい。

  /* identity */
  cairo_identity_matrix( c );
  matrix_print( c );

出力に次が追加されます。

a=1, c=0, x0=0
b=0, d=1, y0=0

前回紹介したcairo_save()とcairo_restore()の組は、座標変換以外の諸々の操作も記憶・復元してしまうので、場合によっては使いにくいかも知れません。代わりにcairo_get_matrix()とcairo_set_matrix()の組を用いれば、座標変換だけを記憶・復元することができます（ただし記憶したい分だけcairo_matrix_t型インスタンスを用意する必要があります）。