Noise2Noise解説とPytorchでの実装
こんにちは!今回はノイズを除去する深層学習モデルについて、特に答えとなる綺麗な画像がない場合でもノイズが除去できる手法であるNoise2Noise(Lehtinen et al., 2018 [1])について勉強したので、Pytorchでの実装を紹介しながら説明したいと思います。
原著論文:Noise2Noise: Learning Image Restoration without Clean Data
最後に参照に記載したようにNoise2Noiseの記事として既にいくつか記事がありますが、自身の勉強のためのアウトプットでもあるのでご容赦頂けると幸いです。
Noise2Noiseとは?
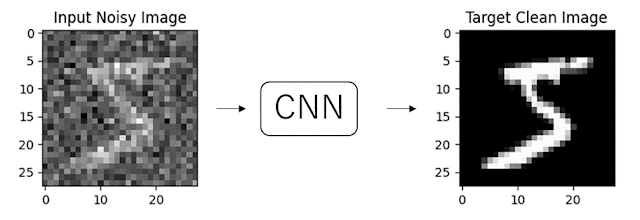
深層学習を用いたノイズ除去モデルの実装を考える際に、最初に思いつくのは学習データとしてノイズ画像とそれに対応するクリーンな画像を用意して、ノイズ画像からクリーンな画像を予測するモデルを作成することだと思います。
CNNを用いたノイズ除去はZhang et al., (2017)[2] 等でその性能の高さが言われています。
しかし現実には、ノイズの含まれるデータは手に入っても、元のクリーンなデータを集めることは難しいことが多いです。 例えば、CTスキャンなどの医療画像は像はしばしばノイズ(機器の誤差や患者の動きによるもの)を含んでいます。しかし、ノイズがない「クリーンな」画像を取得することは、技術的にも倫理的にも困難です。
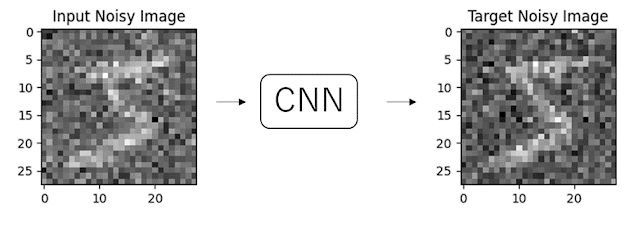
Noise2Noise では、クリーンなデータが利用できない状況でも、ノイズ除去を行うことを可能にします。その手法はとても単純で、異なるノイズが加えられたデータをペアとして、モデルの学習を行うというものです。
上図では、右と左の画像は(分かりにくいですが)含まれるノイズが微妙に異なっており、このようにノイズ同士のペアで学習した場合でも、学習したモデルはクリーンな画像を予測するモデルとなります(下図)。
なぜこのようにノイズ画像のみからの学習で、ノイズが含まれる画像をクリーンな画像にすることが可能になるのでしょうか?
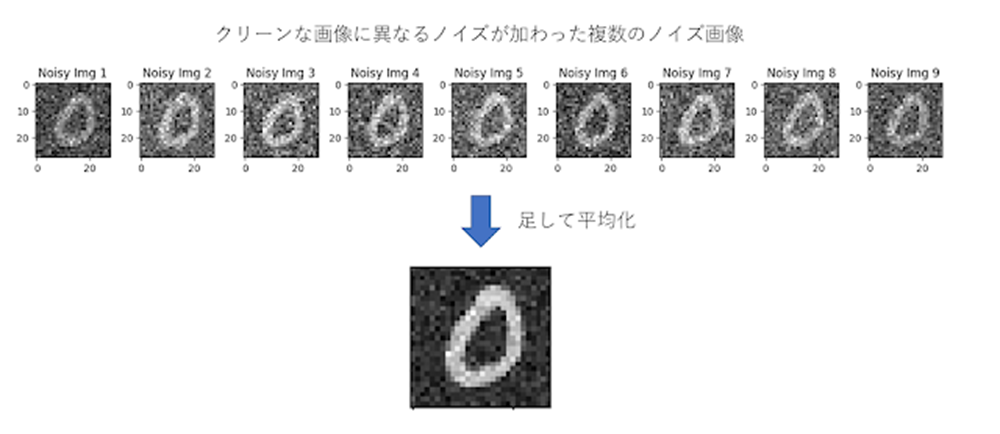
ここで重要なことは、学習に用いるノイズ画像のペアは、その背後に隠れているクリーンな画像は同じもので、それぞれに異なるランダムなノイズが加えられているという点です。
こうした、ノイズ画像が複数ある場合、それぞれ画像を比較すると、正しい信号(MNISTの場合は数字)の部分は同じですが、ノイズ部分は異なります。そのため、それらの画像の足し合わせ平均を取ると正しい信号が浮かび上がり、ノイズは消えていきます。
Noise2Noiseはこのアイデアを活かしたモデルとなっています。
数式による説明
ノイズ画像は元のクリーンなデータ $x$ にノイズ $n$ が加わったものと考えることができます。つまり、ノイズ画像を $y_1$ とすると $y_1 = x + n$ と表すことができます。通常のノイズ除去の問題では、ノイズ画像 $y_1$ から元のクリーンなデータ $x$ を推定することが目標となります。
なお、ここでいうノイズはランダムノイズで、元の画像と相関がないこと、平均が0となるものを仮定しています。
ノイズ除去モデルの学習は、損失関数 $L$ を最小化することによって行われます。損失関数 $L$ は、CNNモデルの出力 $f_\theta(\mathbf{y}_1)$ ともう一つのクリーンデータ $x$ との間の差を測定します。ここで $f_\theta(\mathbf{y}_1)$ の $\theta$ はCNNモデルの重みパラメータを表しており、$\theta$ が変わることで、モデルの出力 $f_\theta(\mathbf{y}_1)$ が変化します。
平均二乗誤差(MSE)を損失関数とした場合、損失関数 $L$ は以下のように定義されます:
$$
L = |f_\theta(\mathbf{y}_1) - \mathbf{x}|_2^2
$$
CNNモデルは学習によりこの損失関数 $L$ が最も小さくなるように重みパラメータ $\theta$ を最適化していきます。この損失関数 $L$ が最小となる場合の $\theta$ は以下のように書くことができます。(ここでは、ノイズ画像からクリーンな画像の変換の際の、最適な重みパラメータを意味するように $\theta_{\mathrm{N} 2 \mathrm{C}}$ とします)
$$
\boldsymbol{\theta}_{\mathrm{N} 2 \mathrm{C}} = \underset{\theta}{\arg \min} \mathbb{E}\left[|f_\theta(\mathbf{y}_1) - \mathbf{x}|_2^2\right]
$$
ここで $\mathbb{E}$ は期待値を表しています。大量のノイズ画像とクリーンな画像を用いて学習をすることで、CNNモデルは重みパラメータを $\theta_{\mathrm{N} 2 \mathrm{C}}$ へと最適化していきます。
次にNoise2Noiseつまりノイズ画像からノイズ画像への変換の場合を考えます。モデルへの入力となるノイズ画像は先ほどと同じ $y_1 = x + n$ です。正解もノイズ画像となるので正解のノイズ画像を $y_2 = x + n'$ とします。ここで $n'$ は $n$ と異なるノイズを加えていることを表しています。この場合CNNモデルが学習によって重みパラメータ $\theta_{\mathrm{N} 2 \mathrm{N}}$ を以下のように最適化します。
$$
\boldsymbol{\theta}_{\mathrm{N} 2 \mathrm{N}} = \underset{\theta}{\arg \min} \mathbb{E}\left[|f_\theta(\mathbf{y}_1) - \mathbf{x} - \mathbf{n'}|_2^2\right]
$$
結論から先に申し上げると、$\theta_{\mathrm{N} 2 \mathrm{N}}$ は $\theta_{\mathrm{N} 2 \mathrm{C}}$ と等しくなります。つまりノイズ画像同士で学習した場合でも、ノイズ画像とクリーンな画像のペアで学習した時と同じようにCNNの重みパラメータは学習されるということです。
本当に等しいのか、確かめてみます。
$$
\begin{eqnarray*}
\boldsymbol{\theta}_{\mathrm{N} 2 \mathrm{~N}} & = &\underset{\theta}{\arg \min }
\mathbb{E}\left[\left|f_\theta\left(\mathbf{y}_1\right)-\mathbf{y}_2\right|_2^2\right] \\ & = &\underset{\theta}{\arg \min } \mathbb{E}\left[\left|f_\theta\left(\mathbf{y}_1\right)-\mathbf{x}-\mathbf{n'}\right|_2^2\right] \\ & = &\underset{\theta}{\arg \min } \mathbb{E}\left[\left|f_\theta\left(\mathbf{y}_1\right)\right|_2^2
+\mathbf{n'}^{\top} \mathbf{n'}
+\mathbf{x}^{\top} \mathbf{x}
-2 \mathbf{x}^{\top} f_\theta\left(\mathbf{y}_1\right)
-2 f_\theta\left(\mathbf{y}_1\right)^{\top} \mathbf{n'}
-2 \mathbf{x}^{\top} \mathbf{n'}\right] \
\end{eqnarray*}
$$
ここで、ノイズはランダムなため元々の画像とは相関がなく独立であるため
$$
\begin{eqnarray*}
\mathbb{E}\left[
\mathbf{x}^{\top} \mathbf{n'}\right] = \mathbb{E}\left[
\mathbf{x}\right] \mathbb{E}\left[\mathbf{n'}\right] \
\end{eqnarray*}
$$
$$
\begin{aligned}
\mathbb{E}\left[
f_\theta\left(\mathbf{y}_1\right)^{\top} \mathbf{n'}\right] = \mathbb{E}\left[
f_\theta\left(\mathbf{y}_1\right)\right] \mathbb{E}\left[\mathbf{n'}\right] \
\end{aligned}
$$
が成り立ちます。
またノイズはランダムでありその平均は0なのでノイズの期待値$\mathbb{E}\left[\mathbf{n'}\right]$ は0になります。
そのため$\mathbb{E}\left[\mathbf{n'}\right]$を含む項は0となり、
$$
\begin{eqnarray*}
\boldsymbol{\theta}_{\mathrm{N} 2 \mathrm{~N}} & = & \underset{\theta}{\arg \min}
\mathbb{E}\left[\left|f_\theta\left(\mathbf{y}_1\right)\right|_2^2-2 \mathbf{x}^{\top} f_\theta\left(\mathbf{y}_1\right)+ \mathbf{x}^{\top} \mathbf{x}\right] \\
& = &\underset{\theta}{\arg \min } \mathbb{E}\left[\left|f_\theta\left(\mathbf{y}_1\right)-\mathbf{x}\right|_2^2\right] \\
& = &\boldsymbol{\theta}_{\mathrm{N} 2 \mathrm{C}}
\end{eqnarray*}
$$
$\theta_{\mathrm{N} 2 \mathrm{C}}$ は $\theta_{\mathrm{N} 2 \mathrm{C}}$ と等しくなり、ノイズ画像同士で学習した場合でも、ノイズ画像とクリーンな画像のペアで学習した時と同じようにCNNの重みパラメータは学習されることが確かめられました。
ただし、$\theta_{\mathrm{N} 2 \mathrm{C}}$ が $\theta_{\mathrm{N} 2 \mathrm{C}}$ と等しくなるには、ノイズは元の画像と相関がなくノイズの平均が0であることが求められているので、こうした条件を満たさないノイズに対してはNoise2Noiseが有効である保証はないということになります。
実装
手書き文字のMNISTに対してノイズ除去を試しました。
Noise2Noiseの前に、ノイズ画像とクリーン画像をペアとした学習(Noise2Clean)を先に実装しています。コラボラトリーを作成しましたので、コード全体に興味ある方は覗いてみてください。
Noise2Clean (ノイズ画像とクリーン画像のペアによる学習)Google Colab
Noise2Noise (ノイズ画像のペアによる学習)Google Colab
Noise2Cleanにおける学習は以下のようなコードとなります。
def train(model, loader, criterion, optimizer):
model.train()
running_loss = 0.0
for images, _ in loader:
images = images.to(device)
noise = torch.randn_like(images)*0.4 #ガウシアンノイズの作成
noisy_images = images+noise #ノイズデータの作成
optimizer.zero_grad()
outputs = model(noisy_images) #モデルの入力はノイズデータ
loss = criterion(outputs, images) #モデルの出力とノイズの無い元の画像の誤差を計算
loss.backward()
optimizer.step()
running_loss += loss.item() * images.size(0)
epoch_loss = running_loss / len(loader.dataset)
return model, optimizer, epoch_loss
元画像(images)にノイズ(noise)を加えノイズ画像(noisy_images)を作成しています。
モデルの学習はノイズ画像を元画像に変換するように行われています。
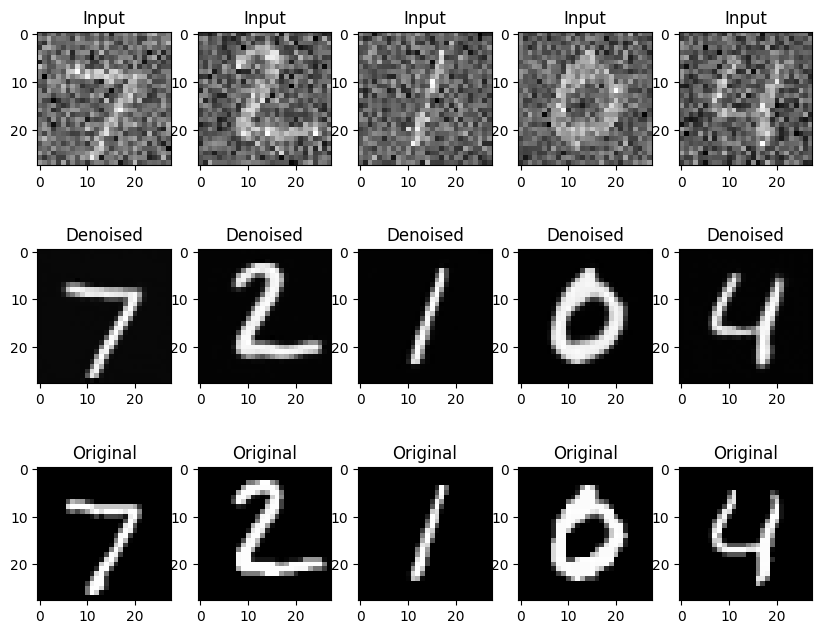
Noise2Cleanの学習の結果は以下のようになります。
上図の一番上の列は入力となるノイズ画像で、真ん中の列が学習したモデルによるノイズ除去の結果、一番下の図がもともとの画像となります。
Noise2Cleanによりノイズ除去がうまくできているかと思います。
次にNoise2Noiseの学習部分のコードになります。
def train(model, loader, criterion, optimizer):
model.train()
running_loss = 0.0
for images, _ in loader:
images = images.to(device)
noise1 = torch.randn_like(images)*0.4
noise2 = torch.randn_like(images)*0.4
noisy_images=images+noise1 #入力となるノイズデータの作成
noisy_images_t=images+noise2 #教師となるノイズデータの作成(変更箇所)。入力データとは異なるノイズが追加されている
optimizer.zero_grad()
outputs = model(noisy_images) #モデルの入力はノイズデータ
loss = criterion(outputs, noisy_images_t) #モデルの出力と教師のノイズデータの誤差を計算(変更箇所)
loss.backward()
optimizer.step()
running_loss += loss.item() * images.size(0)
epoch_loss = running_loss / len(loader.dataset)
return model, optimizer, epoch_loss
Noise2Cleanとほぼ変わりませんが教師画像が先ほどはクリーンな元画像でしたが、今回は教師画像にもノイズ画像(noisy_images_t)が用いられています。
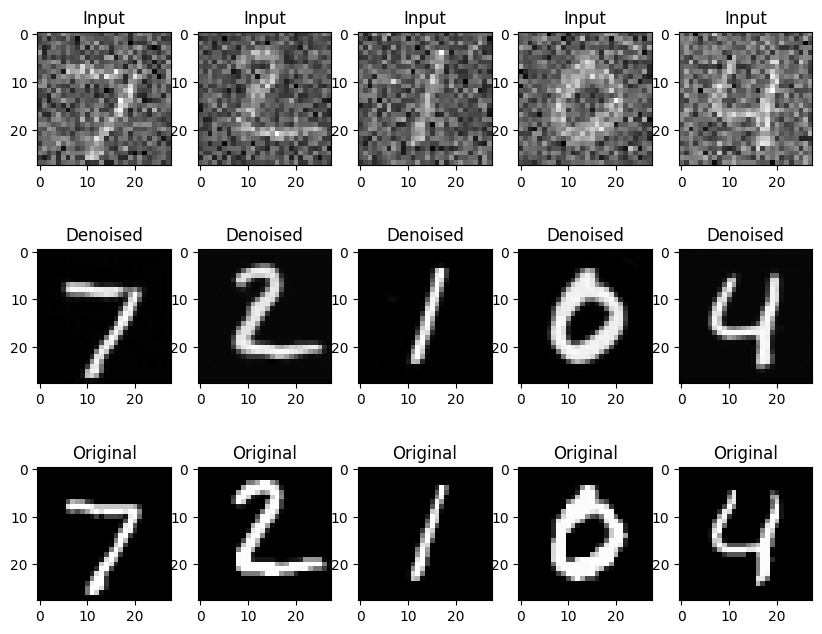
Noise2Noiseの学習の結果は以下のようになります。
学習にクリーンな画像を用いてないにもかかわらず、Noise2Cleanと同じようにノイズ除去ができていることが分かりました。
終わりに
今回、Noise2Noiseという手法を用いてノイズ画像のみを学習に用いて、ノイズ画像から元の綺麗な画像を予測するCNNモデルを作成し、結果として、ノイズ画像のみでもノイズ除去が可能であることがわかりました。今回の学習では、Noise2Noiseの損失関数としてMSEを使用しましたが、ノイズの種類によってはそれ以外の損失関数のほうが有効であることもありますので、今後、試していければと思います。
また、Noise2Noiseはノイズ画像のみを学習データを使用するため、クリーンな画像を用意する必要がありませんが、依然としてペアとなるノイズ画像(ノイズを除くと同じ画像)を用意する必要があり、適用範囲は限られます。今後、ペアとなるノイズ画像がなくても、ノイズ画像だけからノイズ除去を学習する手法を紹介できたらと思います。
参照
[1] Lehtinen, Jaakko, et al. "Noise2Noise: Learning image restoration without clean data." arXiv preprint arXiv:1803.04189 (2018).
[2] Zhang, Kai, et al. "Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising." IEEE transactions on image processing 26.7 (2017): 3142-3155.
Noise2Noise解説
ノイズいっぱいの画像だけで学習しても綺麗な画像が復元できる『noise2noise』をpytorchで実装