📗 この記事の目的
Pythonの代数演算ライブラリSymPyと 数値計算用のライブラリであるSciPyやNumPyとの組み合わせが強力であることを示す例として、二重振り子を数値計算で解くということを試みます。
↓二重振り子
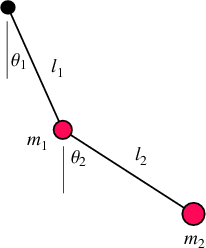
引用元
実は、その単純な見た目からは想像できないほど、二重振り子の極座標での運動方程式は 非常に複雑です。
難しいことで有名な力学の教科書である ランダウ・リフシッツ 力学 でも出てくるぐらい有名な練習問題の一つです。
今回は、Pythonを使ってマシンパワーで、サクッと極座標の運動方程式の導出をしてしまおうというわけです。
注意点
今回の記事は、ゴツイ数式が大量に出てきます。
苦手な方は、最後のGIFアニメーションだけをご覧ください。
あと、**解析力学の知識(特にラグランジアン)**を前提としています。
ただ、知らない方も、今回の記事は、SymPyでの代数演算とSciPyを使った数値計算をPythonという単一の言語でできるのいいね(Python万歳)、というものなので、雰囲気だけでも伝われば幸いです。
「なんかやってんなー」くらいの軽い気持ちで見てください笑
🕰 二重振り子とは?
二重振り子 とは、上記の画像の通り、振り子の先にもう一つ振り子が繋がっているものです。単振り子は非常に単純な運動をしますが、そのさきにもう一つの振り子がついただけの二重振り子は カオスな振る舞い をすることが知られています。
カオス というのは、数学的には細かい定義があるものの、その特徴を大雑把にいうと、
- 初期値の小さなずれが結果的に大きなずれになること(初期値鋭敏性)
- 周期的でないこと
- 非線形であること
の3つです。
特に、初期値鋭敏性があるおかげで、二重振り子は全く予想ができない動きをします。
運動方程式を導出した後は、ついでにこれもシミュレーションしてみましょう。
本記事の流れ
- モデル設定
- 極座標のラグランジアンを導出
- 極座標の運動方程式を導出
- シミュレーション
✏️ モデル設定
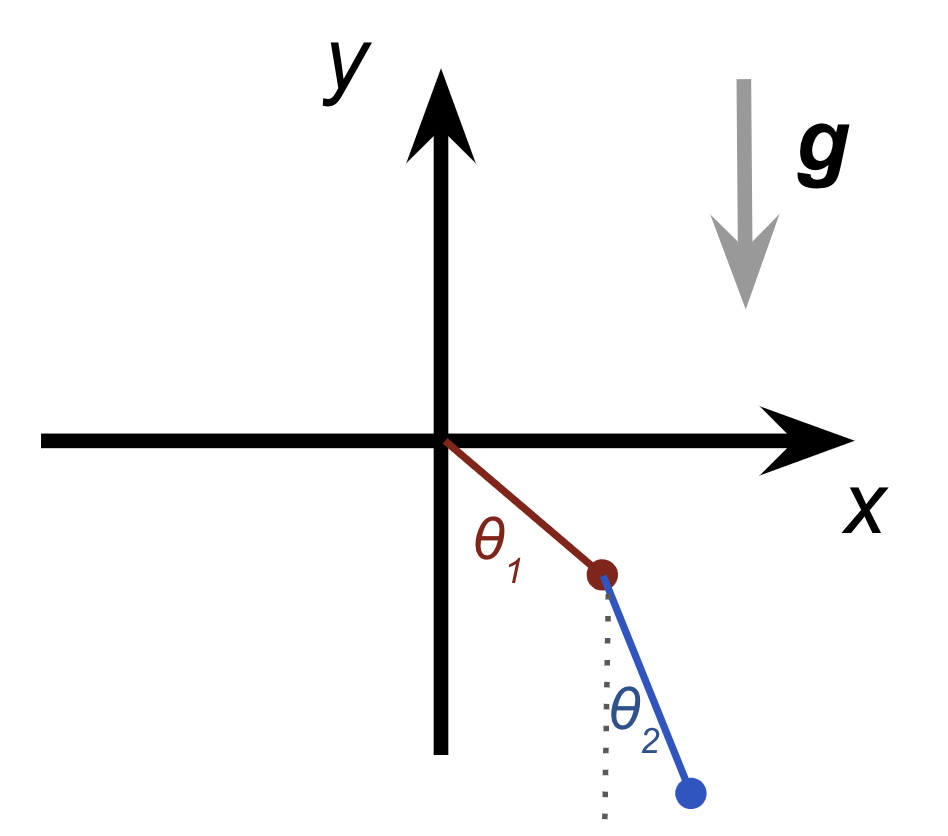
水平にx軸、鉛直上向きにy軸があり、y軸負方向に重力がかかっています。
また、原点から長さ$r_1$の棒の先に1つ目の質点がついていて、そこから長さ$r_2$の棒で2つ目の質点がつながっているとします。
それぞれの棒がy軸とのなす角をそれぞれ$\theta_1, \theta_2$とします。
SymPyをimportします。
import sympy as sy
sy.init_printing()
sy.init_printing の別オプションについては、
SymPyで代数演算してみるを参照してください。
📚 文字変数や関数を定義
# 変数と関数を定義
t = sy.Symbol("t", real=True)
r1, r2, m1, m2, g = sy.symbols(r"r_1 r_2 m_1 m_2 g", positive=True)
# theta1, theta2 = sy.symbols(r"\theta_1 \theta_2", real=True)
theta1 = sy.Function(r"\theta_1")(t)
theta2 = sy.Function(r"\theta_2")(t)
theta1_dot, theta2_dot = sy.symbols(r"\dot{\theta_1} \dot{\theta_2}")
🎈 ラグランジアンの極座標表示を導出
ラグランジアンの最大の特徴は、座標変換不変です。
したがって、デカルト座標でラグランジアンを作った後、それを極座標の変数で表します。
- 質点の位置・速度を極座標で表す
- デカルト座標表示のラグランジアンを座標変換(デカルト座標->極座標)して、ラグランジアンを極座標表示する
質点の位置・速度を極座標で表す
# 質点1の位置と速度
x1 = sy.Matrix([r1 * sy.sin(theta1), - r1 * sy.cos(theta1)])
v1 = x1.diff(t)
x1
$$\left[\begin{matrix}r_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)}, - r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)}\end{matrix}\right]$$
v1
$$\left[\begin{matrix}r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)}, r_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)}\end{matrix}\right]$$
# 質点2の位置と速度
x2 = x1 + sy.Matrix([r2 * sy.sin(theta2), - r2 * sy.cos(theta2)])
v2 = x2.diff(t)
x2
$$\left[\begin{matrix}r_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} + r_{2} \sin{\left(\theta_{2}{\left(t \right)} \right)}, - r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)} - r_{2} \cos{\left(\theta_{2}{\left(t \right)} \right)}\end{matrix}\right]$$
v2
$$\left[\begin{matrix}r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} + r_{2} \cos{\left(\theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{2}{\left(t \right)},
r_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} + r_{2} \sin{\left(\theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{2}{\left(t \right)}\end{matrix}\right]$$
デカルト座標表示のラグランジアンを座標変換(デカルト座標->極座標)して、ラグランジアンを極座標表示する
まずは、運動エネルギーを求めます。
# 運動エネルギー
T1 = (m1 * (v1[0]**2 + v1[1]**2) / 2).simplify()
T2 = (m2 * (v2[0]**2 + v2[1]**2) / 2).simplify()
T1
$$\frac{m_{1} r_{1}^{2} \left(\frac{d}{d t} \theta_{1}{\left(t \right)}\right)^{2}}{2}$$
T2
$$\frac{m_{2} \left(r_{1}^{2} \left(\frac{d}{d t} \theta_{1}{\left(t \right)}\right)^{2} + 2 r_{1} r_{2} \cos{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} \frac{d}{d t} \theta_{2}{\left(t \right)} + r_{2}^{2} \left(\frac{d}{d t} \theta_{2}{\left(t \right)}\right)^{2}\right)}{2}$$
次に、ポテンシャルを求めます。
# ポテンシャル
V1 = m1 * g * x1[1]
V2 = m2 * g * x2[1]
V1
$$- g m_{1} r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)}$$
V2
$$g m_{2} \left(- r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)} - r_{2} \cos{\left(\theta_{2}{\left(t \right)} \right)}\right)$$
運動エネルギーとポテンシャルが求まったので、ラグランジアン $L(\theta_1, \theta_2, \dot{\theta_1}, \dot{\theta_2})$ を得ることができます。
L = T1 + T2 - V1 - V2
L
$$g m_{1} r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)} - g m_{2} \left(- r_{1} \cos{\left(\theta_{1}{\left(t \right)} \right)} - r_{2} \cos{\left(\theta_{2}{\left(t \right)} \right)}\right) + \frac{m_{1} r_{1}^{2} \left(\frac{d}{d t} \theta_{1}{\left(t \right)}\right)^{2}}{2} + \frac{m_{2} \left(r_{1}^{2} \left(\frac{d}{d t} \theta_{1}{\left(t \right)}\right)^{2} + 2 r_{1} r_{2} \cos{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} \frac{d}{d t} \theta_{2}{\left(t \right)} + r_{2}^{2} \left(\frac{d}{d t} \theta_{2}{\left(t \right)}\right)^{2}\right)}{2}$$
だんだん結果は複雑になってきましたが、人間側は相当楽をしています。
🐻 ラグランジアンから極座標の運動方程式を求める
さて、この辺りから本格的に ゴツイ数式 になってきます。
ラグランジアンから運動方程式はそれぞれ、
$$\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta_1}}=\frac{\partial L}{\partial \theta_1}$$
$$\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta_2}}=\frac{\partial L}{\partial \theta_2}$$
となるので、
# 質点1の運動方程式
EOM_1 = sy.Eq(L.diff(theta1.diff(t)).diff(t), L.diff(theta1))
EOM_1
$$m_{1} r_{1}^{2} \frac{d^{2}}{d t^{2}} \theta_{1}{\left(t \right)} + \frac{m_{2} \left(2 r_{1}^{2} \frac{d^{2}}{d t^{2}} \theta_{1}{\left(t \right)} - 2 r_{1} r_{2} \left(\frac{d}{d t} \theta_{1}{\left(t \right)} - \frac{d}{d t} \theta_{2}{\left(t \right)}\right) \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{2}{\left(t \right)} + 2 r_{1} r_{2} \cos{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \theta_{2}{\left(t \right)}\right)}{2} = - g m_{1} r_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} - g m_{2} r_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} - m_{2} r_{1} r_{2} \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} \frac{d}{d t} \theta_{2}{\left(t \right)}$$
# 質点2の運動方程式
EOM_2 = sy.Eq(L.diff(theta2.diff(t)).diff(t), L.diff(theta2))
EOM_2
$$\frac{m_{2} \left(- 2 r_{1} r_{2} \left(\frac{d}{d t} \theta_{1}{\left(t \right)} - \frac{d}{d t} \theta_{2}{\left(t \right)}\right) \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} + 2 r_{1} r_{2} \cos{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \theta_{1}{\left(t \right)} + 2 r_{2}^{2} \frac{d^{2}}{d t^{2}} \theta_{2}{\left(t \right)}\right)}{2} = - g m_{2} r_{2} \sin{\left(\theta_{2}{\left(t \right)} \right)} + m_{2} r_{1} r_{2} \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \frac{d}{d t} \theta_{1}{\left(t \right)} \frac{d}{d t} \theta_{2}{\left(t \right)}$$
運動方程式が求められましたが、数値計算まで見越すと、もう少し単純な式にしたいですね。
$\ddot{\theta_1}, \ddot{\theta_2}$について解くと、時間についての2階連立常微分方程式が得られます。
EOMs = sy.solve([EOM_1, EOM_2], (theta1.diff(t, 2), theta2.diff(t, 2)))
EOMs
$\ddot{\theta}_1$ について解いたものは、
$$\frac{g m_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} + \frac{g m_{2} \sin{\left(\theta_{1}{\left(t \right)} - 2 \theta_{2}{\left(t \right)} \right)}}{2} + \frac{g m_{2} \sin{\left(\theta_{1}{\left(t \right)} \right)}}{2} + \frac{m_{2} r_{1} \sin{\left(2 \theta_{1}{\left(t \right)} - 2 \theta_{2}{\left(t \right)} \right)} \left(\frac{d}{d t} \theta_{1}{\left(t \right)}\right)^{2}}{2} + m_{2} r_{2} \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \left(\frac{d}{d t} \theta_{2}{\left(t \right)}\right)^{2}}{r_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} - m_{2}\right)}$$
$\ddot{\theta}_2$ について解いたものは、
$$\frac{\left(m_{1} + m_{2}\right) \left(g \sin{\left(\theta_{2}{\left(t \right)} \right)} - r_{1} \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \left(\frac{d}{d t} \theta_{1}{\left(t \right)}\right)^{2}\right) - \left(g m_{1} \sin{\left(\theta_{1}{\left(t \right)} \right)} + g m_{2} \sin{\left(\theta_{1}{\left(t \right)} \right)} + m_{2} r_{2} \sin{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} \left(\frac{d}{d t} \theta_{2}{\left(t \right)}\right)^{2}\right) \cos{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)}}{r_{2} \left(- m_{1} + m_{2} \cos^{2}{\left(\theta_{1}{\left(t \right)} - \theta_{2}{\left(t \right)} \right)} - m_{2}\right)}$$
軽く引くぐらいゴツくなりましたが、計算は一瞬で終わります。
さて、2元2階常微分方程式は、変数を増やすことで4元1階連立方程式に帰着できますね。
変数は、 $\theta_1$, $\theta_2$, $\dot{\theta}_1$, $\dot{\theta}_2$ の4つとなります。
# 関数を変数に置き換える
t1, t2 = sy.symbols(r"\theta_1 \theta_2")
diff2dot = [(theta1.diff(t), theta1_dot),
(theta2.diff(t), theta2_dot)]
theta1_ddot = EOMs[theta1.diff(t, 2)].subs(diff2dot).subs([(theta1, t1), (theta2, t2)])
theta2_ddot = EOMs[theta2.diff(t, 2)].subs(diff2dot).subs([(theta1, t1), (theta2, t2)])
これでようやく、運動方程式が導出できました!
💻 シミュレーションしてみよう!
SymPyで延々代数演算してきましたが、いよいよお役御免です。
数値演算をするために、上で求めた数式を numpy.ufunc に変換します。
何やってるかというと、
代数的数式 -> 数値計算用の関数
ですね。
# 運動方程式(の右辺)をNumPyの関数に変換する
args = (t1, t2, theta1_dot, theta2_dot, m1, m2, r1, r2, g)
func1 = sy.lambdify(args, theta1_ddot, "numpy")
func2 = sy.lambdify(args, theta2_ddot, "numpy")
数値計算に必要な運動方程式 func1 func2 が求められたので、サクッと数値計算してみましょう。
ここでは、 scipy.integrate.ode という常微分方程式のソルバを使います。
データ処理のところでPandasを使っています。
# 数値計算
from scipy.integrate import ode
def time_evolve(t, y, params):
theta1, theta2, theta1_dot, theta2_dot = y
return [theta1_dot, theta2_dot,
func1(*y, *params),
func2(*y, *params)]
y0 = [np.pi * 1.01, np.pi * 1.01, 0, 0]
params = {"m1": 1, "m2": 1, "r1": 0.1, "r2": 0.1, "g": 9.8}
solver = ode(time_evolve).set_initial_value(y0, 0).set_f_params(params.values())
dt = 0.01
tmax = 100
results = []
while solver.t < tmax:
y = solver.integrate(solver.t + dt)
results.append([solver.t, *y])
# Pandasでデータを扱いやすくする
import pandas as pd
results = pd.DataFrame(results, columns=["t", "theta1", "theta2", "theta1_dot", "theta2_dot"])
results["x1"] = params["r1"] * np.sin(results.theta1)
results["x2"] = results.x1 + params["r2"] * np.sin(results.theta2)
results["y1"] = -params["r1"] * np.cos(results.theta1)
results["y2"] = results.y1 - params["r2"] * np.cos(results.theta2)
データが得られたので、これをGIFアニメーションで出力してみます。
matplotlib.animation を使えば簡単にGIFを作成できます(imagemagickはインストールが必要)。
import matplotlib.animation as animation
import matplotlib.patches as patches
def gen():
for i, vals in results[["t", "x1", "x2", "y1", "y2"]].iterrows():
yield vals.values
def plot_double_pendulum(data):
t, x1, x2, y1, y2 = data
ax.cla()
R = params["r1"] + params["r2"]
ax.set_xlim(-R, R)
ax.set_ylim(-R, R)
ax.scatter([x1, x2], [y1, y2])
ax.add_patch(patches.Arrow(0, 0, x1, y1, width=0.01))
ax.add_patch(patches.Arrow(x1, y1, (x2-x1), (y2-y1), width=0.01))
ax.set_aspect("equal")
fig, ax = plt.subplots()
ani.save("double_pendulum.gif", writer="imagemagick", dpi=100)
plt.show()
🎥 結果
出力したGIFがこちらです。かなり予想しづらい動きをしていることがわかりますね。
🎉 まとめ
この二重振り子のカオス性を試すところまではやっていません。
例えば、 初期値鋭敏性 を調べるためには、ほんの少しだけ初期値をずらしたものをシミュレートし、その差がだんだんと大きくなる様子を見れれば良さそうです。
興味がある方は、この辺りを自分の目で確かめて欲しいと思います。
参考になれば幸いです!
コードをまとめると
本記事のコードをまとめると以下のように書けます。これだけみると単純ですね。
import sympy as sy
# 変数と関数を定義
t = sy.Symbol("t", real=True)
r1, r2, m1, m2, g = sy.symbols(r"r_1 r_2 m_1 m_2 g", positive=True)
# theta1, theta2 = sy.symbols(r"\theta_1 \theta_2", real=True)
theta1 = sy.Function(r"\theta_1")(t)
theta2 = sy.Function(r"\theta_2")(t)
theta1_dot, theta2_dot = sy.symbols(r"\dot{\theta_1} \dot{\theta_2}")
# 質点1の位置と速度
x1 = sy.Matrix([r1 * sy.sin(theta1), - r1 * sy.cos(theta1)])
v1 = x1.diff(t)
# 質点2の位置と速度
x2 = x1 + sy.Matrix([r2 * sy.sin(theta2), - r2 * sy.cos(theta2)])
v2 = x2.diff(t)
# 運動エネルギー
T1 = (m1 * (v1[0]**2 + v1[1]**2) / 2).simplify()
T2 = (m2 * (v2[0]**2 + v2[1]**2) / 2).simplify()
# ポテンシャル
V1 = m1 * g * x1[1]
V2 = m2 * g * x2[1]
# ラグランジアン
L = T1 + T2 - V1 - V2
# 質点1、2の運動方程式
EOM_1 = sy.Eq(L.diff(theta1.diff(t)).diff(t), L.diff(theta1))
EOM_2 = sy.Eq(L.diff(theta2.diff(t)).diff(t), L.diff(theta2))
# 加速度について解く
EOMs = sy.solve([EOM_1, EOM_2], (theta1.diff(t, 2), theta2.diff(t, 2)))
# 関数を変数に変換
t1, t2 = sy.symbols(r"\theta_1 \theta_2")
diff2dot = [(theta1.diff(t), theta1_dot),
(theta2.diff(t), theta2_dot)]
theta1_ddot = EOMs[theta1.diff(t, 2)].subs(diff2dot).subs([(theta1, t1), (theta2, t2)])
theta2_ddot = EOMs[theta2.diff(t, 2)].subs(diff2dot).subs([(theta1, t1), (theta2, t2)])
# NumPy関数化
args = (t1, t2, theta1_dot, theta2_dot, m1, m2, r1, r2, g)
func1 = sy.lambdify(args, theta1_ddot, "numpy")
func2 = sy.lambdify(args, theta2_ddot, "numpy")
# 数値計算
from scipy.integrate import ode
def time_evolve(t, y, params):
theta1, theta2, theta1_dot, theta2_dot = y
return [theta1_dot, theta2_dot,
func1(*y, *params),
func2(*y, *params)]
# 初期値
y0 = [np.pi * 1.01, np.pi * 1.01, 0, 0]
params = {"m1": 1, "m2": 1, "r1": 0.1, "r2": 0.1, "g": 9.8}
solver = ode(time_evolve).set_initial_value(y0, 0).set_f_params(params.values())
dt = 0.1
tmax = 50
results = []
# 微分方程式を解く
while solver.t < tmax:
y = solver.integrate(solver.t + dt)
results.append([solver.t, *y])
import pandas as pd
results = pd.DataFrame(results, columns=["t", "theta1", "theta2", "theta1_dot", "theta2_dot"])
results["x1"] = params["r1"] * np.sin(results.theta1)
results["x2"] = results.x1 + params["r2"] * np.sin(results.theta2)
results["y1"] = -params["r1"] * np.cos(results.theta1)
results["y2"] = results.y1 - params["r2"] * np.cos(results.theta2)