SymPyとは
代数演算のライブラリです。
Symbolicな演算(文字を数値としてではなくそのまま計算する演算)を可能にします。
SymPyでできること
- 文字変数定義
- 正負
- 実数、複素数
- 展開
- 因数分解
- 極限
- 微分
- 積分
- 方程式を解く
- 行列演算
前準備
ModuleNotFoundError が出る場合は、 pip install sympy してください。
import sympy as sy
# Jupyter Notebook上で、レンダリングされた結果を表示する
sy.init_printing()
出力結果の例:
$$x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}$$
sy.init_printing の設定次第で、様々な形式で演算結果を表示することができます
参考資料
レンダリングせず、latexコードを出力する場合
# 第一引数: レンダリングしない
# str_printer: 出力結果をsy.latexでラップして、latex出力に変換する
sy.init_printing(False, str_printer=lambda x: sy.latex(x))
出力結果の例: x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}
このように設定すると、Jupyter Notebookの出力が全てlatexコードに変換されます。
論文やレポートなどに貼り付ける場合、最初はレンダリング結果をみながらコードを修正し、最後はlatex出力するのが便利そうですね。
ちなみに、 sy.latex 関数は、数式をlatex出力する関数です。
レンダリングをしたくない場合
sy.init_printing(False)
出力結果の例: x3 + 3*x2y + 3x*y2 + y3
これは、Pythonの文法で出力したいときに使います。これをこのままコピペしたらSymPyで使えます。
基本的な使い方
シンボルの定義
# シンボルを定義
a = sy.Symbol("a")
a
$$a$$
# 複数のシンボルを同時に定義
x, y = sy.symbols("x y")
# LaTexの記法を使える(raw文字列にしないとエスケープ文字と認識する)
theta, gamma = sy.symbols(r"\theta \gamma")
theta, gamma
$$\left( \theta, \ \gamma\right)$$
# 正の実数として定義
r = sy.Symbol("r", positive=True)
# 実数として定義
q = sy.Symbol("q", real=True)
文字の情報を与えないと非常に一般的な複素数として計算することがあるので、なるべく情報を与えるようにしましょう。
基本演算
a**2 + x - theta
$$- \theta + a^{2} + x$$
a**2 / a
$$a$$
(x + y)**3
$$\left(x + y\right)^{3}$$
式の展開など
f = (x + y)**3
f.expand()
$$x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}$$
# x^2の係数
f.expand().coeff(x, n=2)
$$3 y$$
微分や極限
f = sy.sin(x)/x
f.limit(x, 0)
$$1$$
# xで偏微分
f = 3 * x**2 * y + x * y**2
f.diff(x)
$$6 x y + y^{2}$$
代入(シンボルも代入できる)
# y に a**2 を代入
f.subs([(y, a**2)])
$$a^{4} x + 3 a^{2} x^{2}$$
NumPyのufuncに変換
シンボリックな表現をNumPyのufuncに変換できます。
これは結構便利です。
シンボリックな計算をしたあと、数値計算を簡単にすることができます。
x, a, b, c = sy.symbols("x a b c")
f = a * x**2 + b * x + c
f
$$a x^{2} + b x + c$$
# 4引数を持つ関数を定義
args = (x, a, b, c)
func = sy.lambdify(args, f, "numpy")
func は、4変数関数です。
ただし、 $a$, $b$, $c$ を固定すれば二次関数となりますね。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
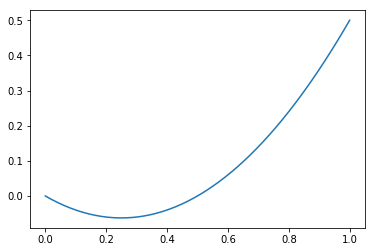
# 実際に数値を代入(ufuncとして振る舞い、ベクトル演算が可能)
xx = np.linspace(0, 1)
plt.plot(xx, func(xx, 1, -0.5, 0))
plt.show()
方程式を解く
eq = sy.Eq(2*x + 5*y, -1)
$$2 x + 5 y = -1$$
sy.solve(eq, x)
$$- \frac{5 y}{2} - \frac{1}{2}$$
まとめ
Jupyter Notebookでの出力方法と、基本的な使い方を紹介しました。
SymPyを使えば、代数演算をマシンパワーを使ってガンガン計算できるようになります。
今までケアレスミスに怯えながら計算していた複雑な計算も、SymPyで検算することができるようになったり、人間では到底できない計算もできるため、いろんな可能性が広がりますね。
行列演算などは、他にも記事を書いてみたいと思います。