Sympy+Jupyterで最強の電卓環境を作る

Sympy + Jupyterで最強の電卓環境を作ってみましょう。

Sympyとは？

SympyはPythonで書かれた代数計算ライブラリで、MathematicaやMaximaみたいなものと思ってください。
Pythonで数式を書けるのでプログラマにとってはこちらの方が使いやすいです、下記のページは素晴らしいSympy入門です、Sympyを知らない方はご一読ください。

3.2. Sympy : Python での代数計算

JupyterからSympyを使う

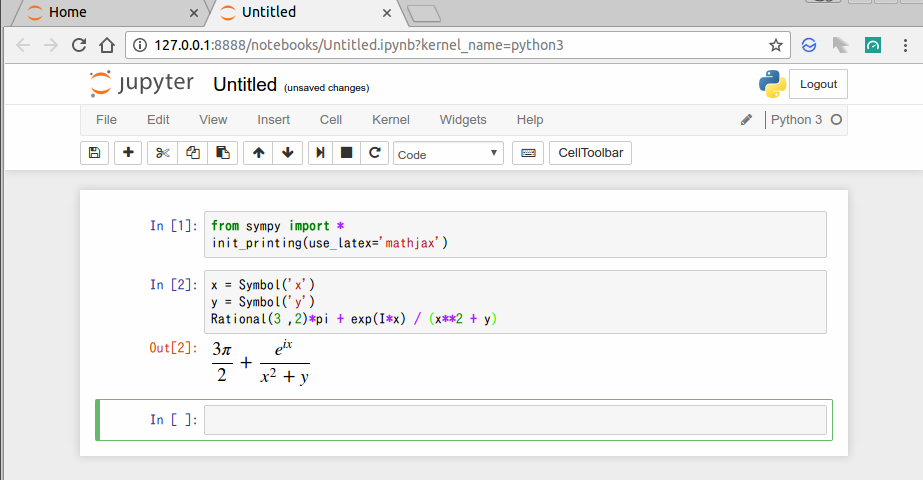
特に特別な事をする必要はないのですが、Jupyterの最初のセルに数式とグラフを表示するために'おまじない'を打ちます。

from sympy import *
init_printing()

次に数式を打ってみましょう。

x = Symbol('x')
y = Symbol('y')
Rational(3 ,2)*pi + exp(I*x) / (x**2 + y)

$$\frac{3 \pi}{2} + \frac{e{i x}}{x{2} + y}$$

数式が出れば成功です。

init_session()について

@void99_ さんからの情報でinit_printingよりも高機能なinit_sessionというものがあるそうです。

from sympy import *
init_session()

よく使う変数、関数があらかじめ定義されます、便利ですね。

IPython console for SymPy 1.0 (Python 3.5.2-64-bit) (ground types: python)

These commands were executed:
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

Documentation can be found at http://docs.sympy.org/1.0/

シンボルの設定

数式のシンボルは`Symbol'で設定できます。

x = Symbol('x')
y = Symbol('y')

複数のシンボルはsymbolsを使えば、一気に設定も可能です。

x, y = symbols("x y")

他にもsympy.abcモジュールを使って設定も可能です。

from sympy.abc import x, y

数式の簡素化

電卓として扱う場合に一番便利な機能は数式の簡素化でしょう、数式をこねくりまわしているとすごく長い数式ができてしまうのですが、Sympyを使えば一発です。

例えば以下の数式があったとしましょう。
この数式は、たしか私がベジェ曲線の数式か何かこねくりまわして出た数式です。

(A-B)*C + B**2 + (-B-A)*C + B**2

Sympyで書くと以下のようになります。

from sympy.abc import A, B, C
f = (A-B)*C + B**2 + (-B-A)*C + B**2

2 B^{2} + C \left(- A - B\right) + C \left(A - B\right)

Sympyに式を代入すると、見やすいように項を並び替えてくれます。
さらに数式の簡素化したい場合はsimpflyを使います。

simplify(f)

2 B \left(B - C\right)

Aが消えて、ものすごく簡素になりましたね。
Maximaでよく使うratsimpも使えます。

ratsimp(f)

2 B^{2} - 2 B C

式の簡素化には色々な種類があります、詳細は以下を参照してください。

方程式を解く

from sympy.abc import A, B, C, D

(A-B)*D + C**2 + (-B-A)*C+B**2

B^{2} + C^{2} + C \left(- A - B\right) + D \left(A - B\right)

上の数式でAについて解きたい場合、solveを使います。

solve((A-B)*D + C**2 + (-B-A)*C+B**2, A)

\left [ \frac{1}{C - D} \left(B^{2} - B C - B D + C^{2}\right)\right ]

式の変数に値を代入する

subsで式の変数に値を代入できます。

f = (A-B)*D + C**2 + (-B-A)*C+B**2

# A,B,Cに値を代入する
f.subs([(A, 10), (B, 20), (C, 30)])

- 10 D + 400

subsの引数は辞書を渡すこともできます。

f.subs({A: 10, B: 20, C: 30})

- 10 D + 400

代入したい変数が1しかない場合は、第1引数に変数、第2引数に値を指定可能です。

f.subs(A, 10)

B^{2} + C^{2} + C \left(- B - 10\right) + D \left(- B + 10\right)

微分/偏微分

微分/偏微分はdiffを使います。

diff(x**2 + 3*x + 100)

2 x + 3

偏微分の場合は第2引数を指定します。

diff(3*x**2 + 3*x*y + y**2, x)

6 x + 3 y

因数分解/素因数分解

因数分解はfactorを使います。

factor(x**2-x-6)

\left(x - 3\right) \left(x + 2\right)

素因数分解はfactorintを使います。

factorint(3417)
>>> {3:1,17:1,67:1}

辞書が返ってます、3^1 * 17^1 * 67^1 = 3417という事になります。

行列/ベクトル

Matrixクラスを使います。

Matrix([[1, 0], [0, 1]])

\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]

ベクトルはあるにはあるんですが、使いにくいので1列の行列として扱います。

θ = Symbol("θ")

P = Matrix([2*cos(θ), 2*sin(θ)])

\left[\begin{matrix}2 \cos{\left (θ \right )}\\2 \sin{\left (θ \right )}\end{matrix}\right]

ベクトルの演算をする場合はtranspose関数で転置させます。

transpose(P) * P

\left[\begin{matrix}4 \sin^{2}{\left (θ \right )} + 4 \cos^{2}{\left (θ \right )}\end{matrix}\right]

数式をLatexでコピペする

JupyterとSympyを使えば、出力された数式をQiitaに簡単にコピペできます。
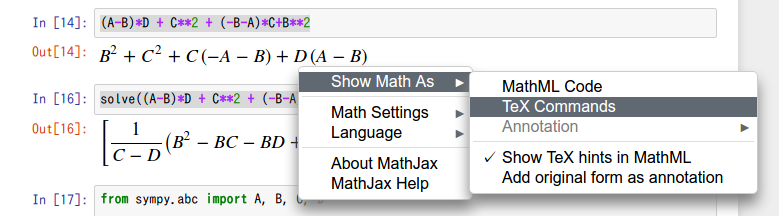
数式を右クリックし「Show Math As」→「Tex Commands」を選択します。

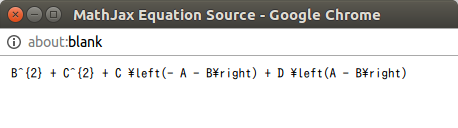
こんなポップアップが出てくるので、数式をコピペします。

このLatexはQiitaにそのまま貼り付け可能なので便利です。

AAで数式を出力する

pprintを使えば、アスキーアート？で数式も出力できます。

pprint(Integral(sqrt(1/x), x), use_unicode=True)
"""
⌠           
⎮     ___   
⎮    ╱ 1    
⎮   ╱  ─  dx
⎮ ╲╱   x    
⌡  
"""

ソースコードに数式を貼り付けるときに便利・・・なんでしょうか。

グラフを書く

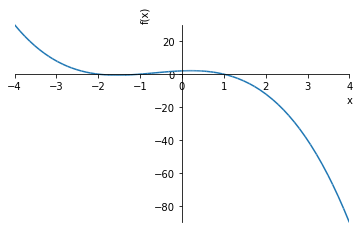
sympy.plotting.plotでグラフを描くことができます。
Sympyの数式をそのまま引数に渡せるので便利です。

from sympy.plotting import plot

y = -(x+2)*(x+1)*(x-1)

# xが-4から4までのグラフを描く
plot(y, (x, -4, 4))

.ipynbのテンプレートで素早く開始する

Jupyter + Sympyはすごく便利なのですが、１セル目におまじないを毎回打ち込まなくてはなりません。
これって意外と面倒なんですよね。

私の記事でPythonでJupyterノートブック「.ipynb」を生成するがあります。
これを使って.最初から色々入力済みのipynbを生成するスクリプトを書いてみましょう。

JupyterとPyCharmの連携

PyCharmはPythonの統合開発環境(IDE)です、非常に強力な補完機能を持っており最強のPython開発環境です。
実はPyCharmはJupyterと連携が可能で、Jupyterの表現力＋PyCharmの強力な補完機能はかなり快適です。

ただし、数式を扱う場合はPyCharmのJupyter出力は貧弱ですので、ブラウザ版のJupyterを使った方がよいでしょう。
ですので、PyCharmのJupyterは使いません、かわりにExtranal Toolsを使います。

.ipynb生成スクリプトを作る

どこか参照しやすい場所に以下のスクリプトを作成します。

#!/usr/bin/env python3
# coding:utf-8
import sys
import os
import nbformat

output_dir = sys.argv[1]
output_file = input("input ipynb name:")

nb = nbformat.v4.new_notebook()

title = "# タイトル"

code = """
%matplotlib inline
from sympy import *
init_session()
"""

nb["cells"] = [
    nbformat.v4.new_markdown_cell(title),
    nbformat.v4.new_code_cell(code)
]

if not output_file.endswith(".ipynb"):
    output_file += ".ipynb"

with open(os.path.join(output_dir, output_file), "w") as f:
    nbformat.write(nb, f)

print("ok.")

PyCharmのExternal Toolとして登録する

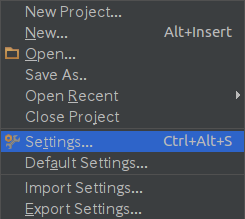
PyCharmの「File(F)」メニューを開き、「Settings...」を選択します。

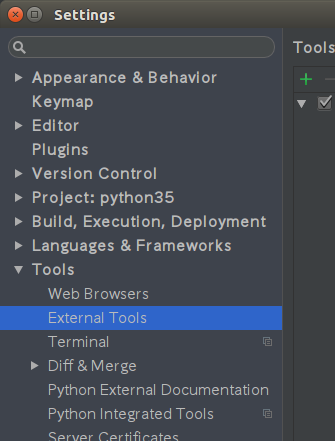
設定ダイアログの「Tools」→「External Tools」を選択して、「＋」ボタンを押します。

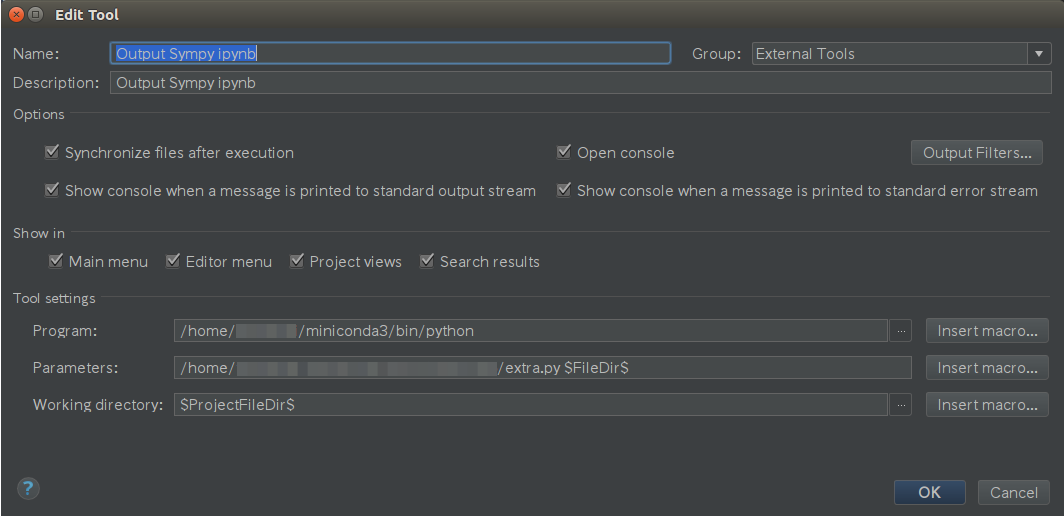
設定ダイアログが出るので、以下の項目を追加します。

項目	入力
Name	適当な名前を入れてください
Description	適当な説明をいれてください
Program	JupyterがインストールされているPythonパス
Parameters	先ほどのスクリプトパス \$FileDir\$

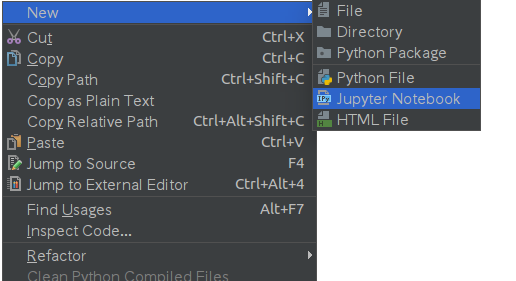
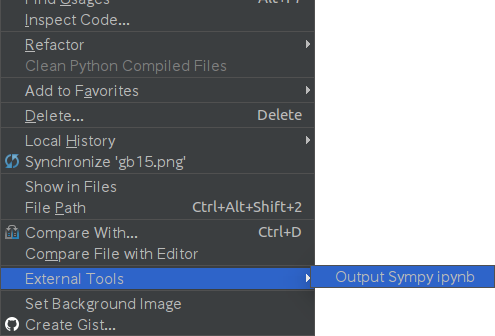
PyCharmの右クリックメニューから.ipynbが生成可能に！

PyCharmの右クリックメニューから「External Toos」→「登録したツール名」を選択します。

コンソールにファイル名を入力すると、最初から色々入力済みの.ipynbファイルが生成されます。

もっと便利な使い方がありましたら、是非とも投稿してください。

あとがき

Sympyよりも.ipynbの出力の方が説明長かったですが、Sympyは非常に便利です。

ゲームプログラマや数式を使う人たちには凄い役に立ちます。
数学が苦手な人にこそ是非とも使ってほしいライブラリです。