numpy で高速に区間列どうしの要素を対応付ける

やりたいこと

一次元の区間(s,t)の集合が2つ(s1 と s2)存在する。
s1中のある要素s1_iが、s2中のどの要素s2_jに対応するかを表現する組合せF (F: s1 -> s2)を作りたい。

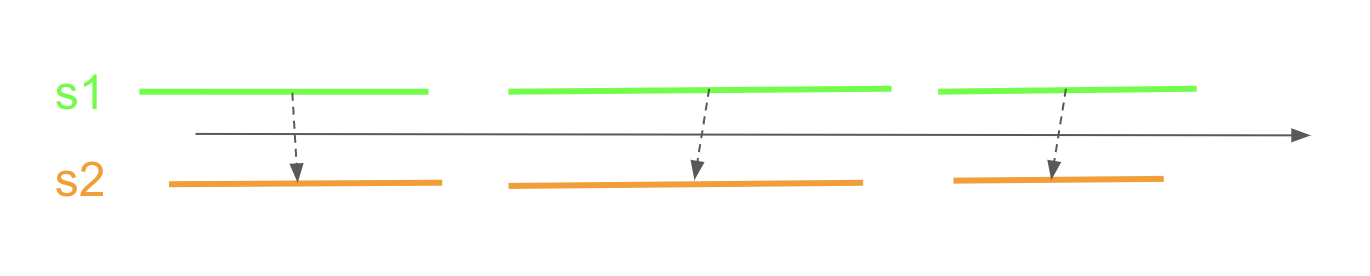
詳細な条件

1. s1 と s2は、それぞれ $10^3$ 個程度の要素を持つ
2. 対応付けは1分以内に完了したい

方針

• 全てのs1_iとs2_jで Intersection over Union (IoU)を計算
  • IoUを一言でいうと、2つの要素における重なりの比率
  • 参照: 【精度指標】IoUとは
    
• s1_iごとに、IoUが最大値となるs2_jを取得する

実装

import numpy as np


def alignment_sequence(s1: np.ndarray, s2: np.ndarray) -> np.ndarray:
    assert s1.shape[1] == 2, f"Expected shape (n, 2), got {s1.shape}"
    assert s2.shape[1] == 2, f"Expected shape (m, 2), got {s2.shape}"

    # strat1, end1: (n, 1)
    start1, end1 = np.expand_dims(s1[:, 0], axis=1), np.expand_dims(s1[:, 1], axis=1)

    # strat2, end2: (1, m)
    start2, end2 = np.expand_dims(s2[:, 0], axis=0), np.expand_dims(s2[:, 1], axis=0)

    # union, intersection, iou_matrix: (n, m)
    union = np.maximum(end1, end2) - np.minimum(start1, start2)
    intersection = np.maximum(np.minimum(end1, end2) - np.maximum(start1, start2), 0)
    iou_matrix = intersection / union
    
    # 最もIoUが高いものを選択
    best_matches = iou_matrix.argmax(axis=1)

    return {
        s1_i: s2_j for s1_i, s2_j in enumerate(best_matches)
    }

ちょっと解説

2つの区間の IoU の求め方

• Intersection (共通部分): "start1とstart2の大きい方" から "end1とend2の小さい方" までの区間
• Union (和集合): "start1とstart2の小さい方" から "end1とend2の大きい方" までの区間
• IoUは、Intersection を Union で除したもの
  

union, intersection, iou_matrix の計算過程

• end1 の形状は (n, 1) で、end2 の形状は (1, m) なので、np.maximum中でブロードキャストされて n x mの全ての要素同士が比較される

np.maximum(end1, end2) # union - end
np.minimum(start1, start2) # union - start
np.minimum(end1, end2) # intersection - end
np.maximum(start1, start2) # intersection - start

使い方

s1 と s2の長さが同じとき

s1 = np.array([[1, 2], [2, 5], [6, 10]])
s2 = np.array([[0, 3], [3, 7], [7, 12]])
alignment = alignment_sequence(s1, s2)
print(alignment)

次の結果が得られる

{0: 0, 1: 1, 2: 2}

s1 と s2の長さが違うのとき

s1 = np.array([[1, 3.2], [3.4, 5.8], [6, 8], [8.1, 10]])  # 4つのセグメント
s2 = np.array([[0, 3], [3.1, 6.1], [6.5, 10]])  # 3つのセグメント
alignment = alignment_sequence(s1, s2)
print(alignment)

次の結果が得られる

{0: 0, 1: 1, 2: 2, 3: 2}

スピードの検証

TODO