IoUとは
Intersection over Union; IoU
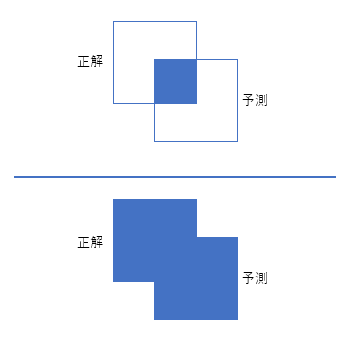
2つの領域がどれくらい重なっているかをあらわす指標。
物体検出やセグメンテーションのタスクで、正解の領域と予測の領域がどれくらい重なっているかをあらわす精度指標として使える。
A:正解領域
B:予測領域
$$
IoU = \frac{A \cap B}{A \cup B}
$$
$\frac{重なっている領域の面積}{2つの領域全体の面積}$となる
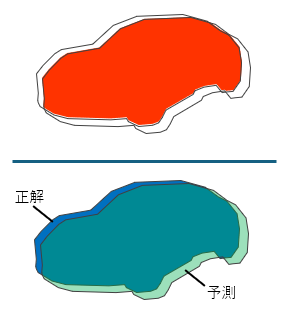
バウンディングボックス
セグメンテーション
物体検出のバウンディングボックス
物体検出のバウンディングについてみてみる
算出
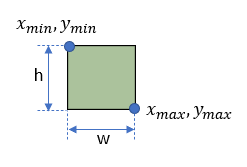
各矩形領域について
- $x_{min}$: 領域左上のx座標
- $y_{min}$: 領域左上のy座標
- $x_{max}$: 領域右下のx座標
- $y_{max}$: 領域右下のy座標
- w: 領域の幅
- h: 領域の高さ
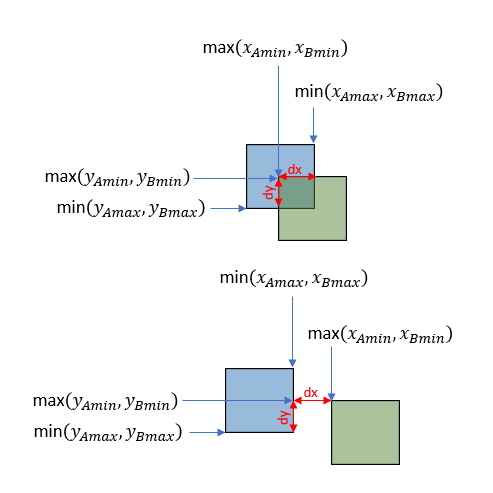
$$dx = min(x_{Amax}, x_{Bmax}) - max(x_{Amin}, x_{Bmin})$$
$$dy = min(y_{Amax}, y_{Bmax}) - max(y_{Amin}, y_{Bmin})$$
$$IoU = \frac{A \cap B}{A \cup B} = \frac{dxdy}{w_Ah_A + w_Bh_B-dxdy}
$$
ただし $ dx \leqq 0 $ または $dy \leqq 0$の場合、$A \cap B$ は0となる。
IoUの値はどんな感じになるか
- 完全一致すると1.0。
- 全く重ならないと0.0。
- 大きめに予測しても、小さめに予測しても、分母となる$A \cup B $が大きくなるので、IoUの値は小さくなる。
- 少しずれても大きくIoUの値が下がる。
完全に一致
| $A\cap B$ | 10,000 |
| $A\cup B$ | 10,000 |
| IoU | 1.0 |
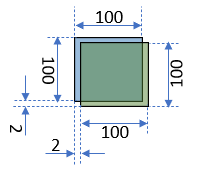
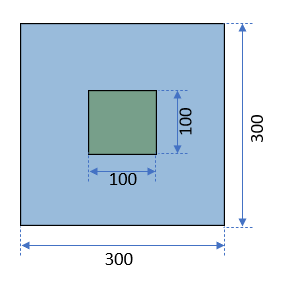
ほぼ一致
| $A\cap B$ | 9,604 |
| $A\cup B$ | 10,397 |
| IoU | 0.924 |
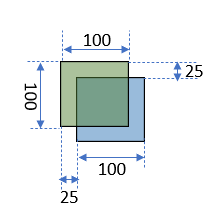
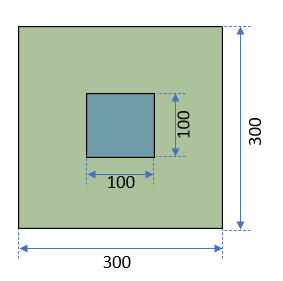
一部一致
この例だと $A\cap B : A\cup B = 9:23 $となっている
| $A\cap B$ | 5,625 |
| $A\cup B$ | 14,375 |
| IoU | 0.391 |
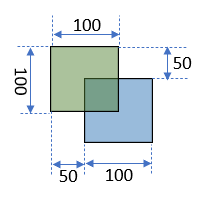
この例だと $A\cap B : A\cup B = 1:7 $となっている
| $A\cap B$ | 2,500 |
| $A\cup B$ | 17,500 |
| IoU | 0.143 |
全く重なっていない
| $A\cap B$ | 0 |
| $A\cup B$ | 20,000 |
| IoU | 0.0 |
すごく大きく予測
| $A\cap B$ | 10,000 |
| $A\cup B$ | 90,000 |
| IoU | 0.111 |
すごく小さく予測
| $A\cap B$ | 10,000 |
| $A\cup B$ | 90,000 |
| IoU | 0.111 |
Pythonサンプル
def calc_iou(a, b):
"""
IoUを算出する。
Args:
a (list[int, int, int, int]) : 矩形Aの情報 [左上のX座標, 左上のY座標, 幅, 高さ]
b (list[int, int, int, int]) : 矩形Bの情報 [左上のX座標, 左上のY座標, 幅, 高さ]
Returns:
float : 算出したIoU
"""
x_a_min, y_a_min = a[:2]
x_a_max = x_a_min + a[2]
y_a_max = y_a_min + a[3]
x_b_min, y_b_min = b[:2]
x_b_max = x_b_min + b[2]
y_b_max = y_b_min + b[3]
dx = min(x_a_max, x_b_max) - max(x_a_min, x_b_min)
dy = min(y_a_max, y_b_max) - max(y_a_min, y_b_min)
if dx < 0 or dy < 0:
intersection = 0
else:
intersection = dx * dy
union = (a[2] * a[3]) + (b[2] * b[3]) - intersection
#print(f"dx: {dx}, dy: {dy}, intersection: {intersection}, union: {union}")
return intersection / union