はじめに

ソーシャルゲームのガチャシステムにおいて、カードの出現確率を表示とは異なる実装にしていたため炎上するといった事件がたびたび発生している。これまでにいくつかの公平なガチャシステムを考えてきたが、今回は従来の公平なガチャシステムに比べてより公平なガチャシステムを考えたので、ここで述べることにする。
この記事を読んで分からないことがある場合や、改良点を思い付いた場合は気軽にコメントして欲しい。

続編を書きました

発表スライド

この記事に関する発表を行った。スライドは次に置かれている。

このスライドのソースコードは次のリポジトリにある。

ソーシャルゲームに実装されたガチャシステム

現在多くのゲームに実装されているガチャシステムは、サーバーサイドで確率の計算が行われる。ユーザーに配布されるゲームはリバースエンジニアリングの手法によって解析される恐れがあるため、クライアントサイドで確率の計算をしてしまうとレアリティの高いカードを不正に入手される可能性があるためである。しかし、サーバーサイドで確率の計算を行なってしまうと、もはやユーザーは確率を知る手段が運営のWebサイトのみになってしまう。すると、運営の実装ミスや恣意的な操作によって確率が間違っていたとしても、ユーザーはそれに気がつくことができずこれは公平ではない。

公平なガチャシステム

公平なガチャシステムとは、次を満たすガチャシステムである。

ユーザーにとっても運営にとってもガチャによるカードの出現確率が明らかである
悪意を持つユーザーや悪意を持つ運営による同意のない確率操作ができない

この記事では、このような定義を持つ公平なガチャシステムについて考える。

既存の公平なガチャシステムとその課題

新しいガチャシステムの説明の前に、従来のガチャシステムを紹介してその問題点を明らかにする。公平なガチャシステムの議論によっていくつかの実現方法があるが、ここでは代表的な二つを取り上げる。

ハッシュ値を用いた公平なガチャシステム

ハッシュ値を用いたガチャシステムにはいくつかのバリエーションがあるが、ここでは最も簡単なものを紹介する。

プロトコル

運営はカード$K_1, K_2, \dots, K_N$とそれに対応するビット列を次のように公開する

ビット列カード

$0000 \dots 1001$ $K_1$

$0010 \dots 0010$ $K_2$

$1110 \dots 0111$ $K_3$

$1011 \dots 1011$ $K_3$

$\vdots$ $\vdots$

$1111 \dots 0100$ $K_N$

また、あるカード$K_i$から対応するビット列を取得するマップ関数を$M$とする
ユーザーのアプリケーションはサーバーへガチャを引くリクエストを送信する
サーバーはソルト$A$とデータ$C$を生成し、データベースにソルト$A$とデータ$C$を保存する
サーバーはアプリケーションにソルト$A$とデータ$C$を送信する
アプリケーションは次を満たす$K_i$が存在するデータ$B$を計算する
```
M(K_i) = C\; \&\; \text{Hash}(A \mid\mid B)
```
アプリケーションはソルト$A$とデータ$B$とカード$K_i$をサーバーへ送信する
サーバーはデータベースからソルト$A$とデータ$C$を取得する

ビット列	カード
$0000 \dots 1001$	$K_1$
$0010 \dots 0010$	$K_2$
$1110 \dots 0111$	$K_3$
$1011 \dots 1011$	$K_3$
$\vdots$	$\vdots$
$1111 \dots 0100$	$K_N$

サーバーは次を検証する

M(K_i) = C\; \&\; \text{Hash}(A \mid\mid B)

サーバーは検証に成功した場合、アプリケーションに成功を送信しカードを付与する

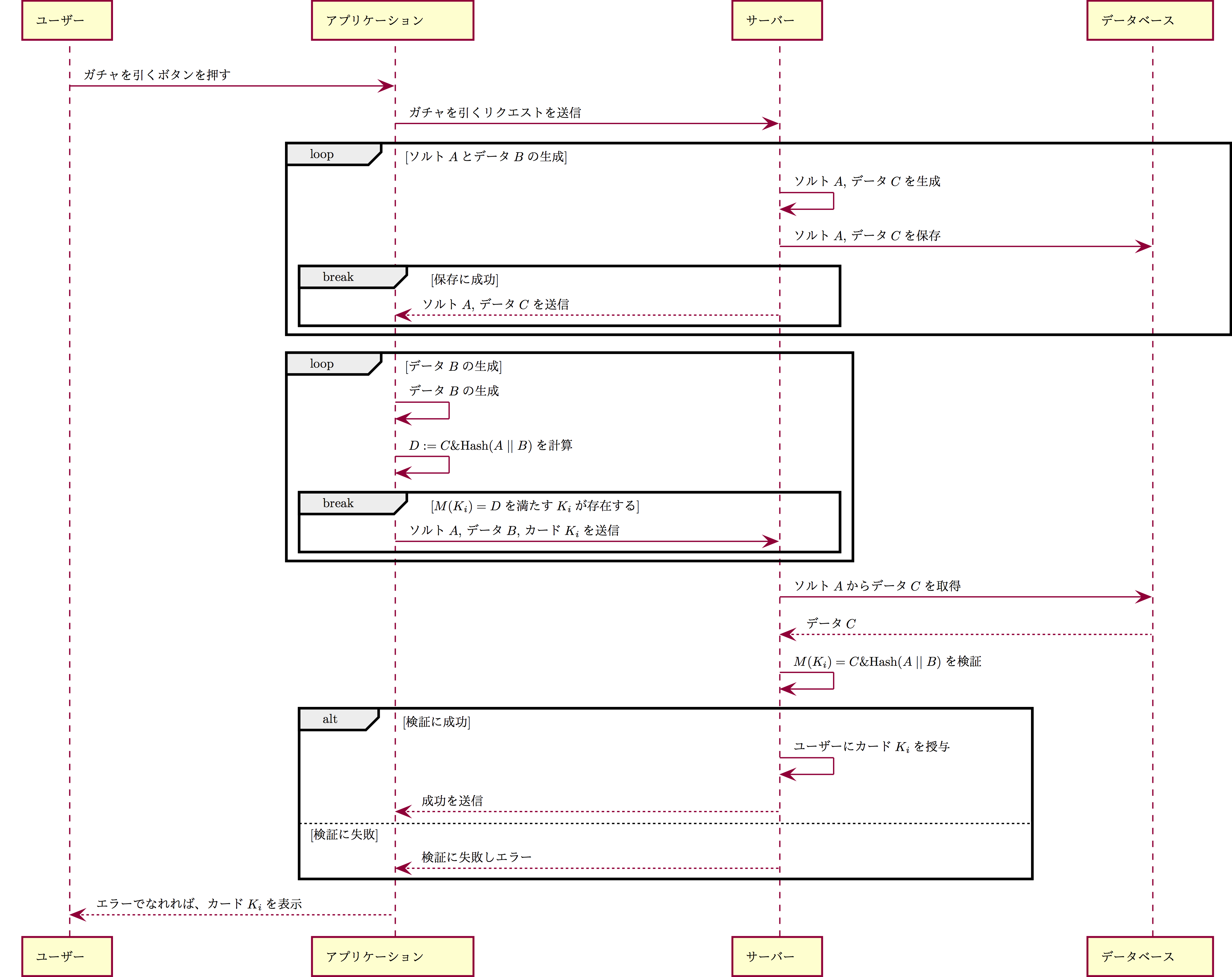
シーケンス図

ハッシュ値を用いたガチャシステムの課題

このガチャシステムは、ハッシュ値が衝突する確率を元にゲームの公平性を担保しているので、ハッシュ値を求める速度が高いほど時間あたりに回せるガチャの数が高くなる。よって、業者などが専用ハードウェアを用いた場合にやや公平とは言えなくなると考えられる。

暗号化を用いた公平なガチャシステム

malaさんが考案したこのガチャシステムは、暗号化によって公平性を保証しようとするものである。なお、malaさんが考えたガチャシステムの全文はGistにアップロードされている。

プロトコル

運営は、$N$種類のカード$K_1 \dots K_N$に番号を割り当てる

カード番号

$K_1$ $1$

$K_2$ $2$

$\vdots$ $\vdots$

$K_N$ $N$
運営は割り当てた番号をシャッフルし、シャッフルした結果をユーザーへ公開する
運営はキーと呼ばれる数値を用意する（ただし、キーは$N$より小さい）
運営はキーを対称鍵暗号で暗号化してユーザーへ送信する
ユーザーは暗号化されたキーを受けとり、(2)でシャッフルされた番号の中から一枚を選択する
運営はキーを暗号化する際に用いた対称鍵をユーザーに公開する
ユーザーは暗号化されたキーを復号し、選択した番号にその数を足して$N$で割った剰余を求める
ユーザーは(7)で求めた剰余に対応するカードを得る

カード	番号
$K_1$	$1$
$K_2$	$2$
$\vdots$	$\vdots$
$K_N$	$N$

暗号化を用いた公平なガチャシステムの課題

サーバーは、キーを暗号化する際に用いた秘密鍵と関係のないデータをさも対称鍵であるかのように偽って、ユーザーへ公表する可能性があるため、このガチャはサーバー（運営）にとって有利なものである。従って、このガチャシステムはこのままでは公平なガチャシステムとは言えない。

コミットメント

新しいガチャシステムを説明する前に、まずはコミットメントについて解説する。
コミットメントを用いることで、ユーザーは値を秘密裏にコミットすることができる。また、ユーザーは後にコミットされた値を明らかにすることが可能である。そして、一度コミットした値を後から変更することは不可能であることが保証されている。
コミットメントは、電話で会話している二人がコイントスで賭けを行うことができるか、という問題を解くための手段と考えると分かりやすい。$A$が裏か表かを宣言して、$B$がコイントスを行って結果を宣言し、$A$の宣言と結果が等しければ$A$の勝ち、そうでなければ$B$の勝ちというゲームである。これを電話で行う場合次のような悪意ある行為が考えられる。

$A$の宣言を聞いた$B$が実際にはコイントスを行なわず、恣意的な結果を主張する

つまりこのゲームは$B$にとって極めて有利だが、コミットメントを用いることで$A$の宣言を秘密にしたまま$B$にコミットできる。そして、$B$がコイントスをして結果を宣言してから、$A$はコミットした値を公開する。この時、一度コミットした値を後から変更することは不可能であるうえ、$B$はコミットされた値から$A$の宣言を知ることはできない。ゆえにコミットメントを用いれば、このコイントスゲームを公平できる。それでは、コミットメントの具体的な方法を説明する。

離散対数に基づくコミットメント

コミットメントには色々な実現方法があるが、ここでは離散対数に基づく方法を紹介する。
ここに二人の人間アリスとボブがいるとする。アリスは文書$m \in \{0, 1, \dots, q - 1\}$をコミットする方法を紹介する。次のようなプロトコルとなる。

ボブは次を満たす素数$p, q$と$\mathbb{Z}_p^{*}$¹から、集合の元の数が$q$となるような部分群$G$から生成元$g$と生成元$v \ne 1$をランダムに選び、$p, q, g, v$を$A$へ送信する
```
p := 2q + 1
```
アリスは次を検証する
- $p, q$が共に素数であり、$p = 2q + 1$であること
- $g, v$が$q$個の元を持つ集合の生成元であること
アリスは乱数$r \in \{0, 1, \dots, q - 1\}$を選ぶ
アリスはボブに$c := g^r v^m$を送信する
公開の際、アリスはボブに$r$と$m$を送信する
ボブは$c = g^r v^m$を検証する

このようにすることで、アリスがコミット後にコミットした値を反故にすることを防げる。

アリスがコミットを反故にできるとすると、アリスが$g^r v^m$をボブに送信しているので、$g^r v^m = g^{r'} v^{m'}$となる$r'$と$m'$を見つけられるということである。しかし、これを仮定した場合、次のような式が成り立ってしまう。

g^r v^m    = g^{r'} v^{m'} \\
v^{m - m'} = g^{r' - r} \\
\log_g(v^{m - m'}) = r' - r \\
\log_g(v) = (r' - r) / (m - m')

つまり$\log_g(v)$を求めており、元$g$と$v$の離散対数問題を解くことは不可能であるということに矛盾する。従って、アリスはコミットを反故にすることはできない。

コミットメントを用いた公平なガチャシステムのプロトコル

ここではmalaさんのガチャを改良して、暗号化ではなくコミットメントを用いたガチャシステムを提案する。この記事で提案する公平なガチャシステムのプロトコルは次のようになる。

運営は、$N$種類のカード$K_1 \dots K_N$に番号を割り当てる

カード番号

$K_1$ $1$

$K_2$ $2$

$\vdots$ $\vdots$

$K_N$ $N$
運営は割り当てた番号をユーザーへ公開する
運営はキーと呼ばれる数値$m$を用意する（ただし、キーは$N$より小さい）
運営はキーのコミットメント$c := g^r v^m$を計算し、$c$をユーザーへ送信する（$g$や$v$、$r$の決め方は離散対数によるコミットメントに基づく）
ユーザーはコミットメント$c$を受けとり、(1)の番号の中から一枚$x$を選択し、$x$を運営へ送信する
運営は$m$と$r$を公開する
ユーザーは$c = g^r v^m$を検証する
ユーザーは選択した番号$x$にキー$m$を足して$N$で割った余り$k$を求める
```
k := (x + m) \bmod N
```
ユーザーは(7)で求めた余り$k$に対応するカードを得る

カード	番号
$K_1$	$1$
$K_2$	$2$
$\vdots$	$\vdots$
$K_N$	$N$

このように対称鍵暗号の代りにコミットメントを用いることで、malaさんのガチャの弱点であった運営の不正を防止できると考えられる。

まとめ

この記事ではより公平なガチャシステムを目指して、コミットメントを用いることでハッシュ値や対称鍵暗号を用いた方法で発生していた微妙な不公平を排除し、より公平なガチャシステムを構築することができた。

参考文献

$\mathbb{Z}_p^{*}$は何らかの$y$が存在して$x = y \bmod p$かつ$xz \equiv 1 \pmod{p}$を満たす逆元$z$が存在する$x$の集合を表す。 ↩