続編
よりよいガチャシステムに関する記事を書きました。
はじめに
前回の記事で説明したハッシュ値の衝突に基づくガチャシステムは、データベースなどといったストレージが必要になる。ユーザーがガチャを引こうとするたびに、アプリケーションがストレージにアクセスするため、悪意のあるユーザーがDoS攻撃などを行う可能性もある。このような場合はCAPTCHAを設置して機械による攻撃を防止するなどが容易に考えられるが、今回はユーザーの識別という作業を暗号技術で代替することによって、そもそも前回の記事に登場したデータ$A$や$B$を保存するストレージを排除したプロトコルを提案する。もしこの記事を読んで分からないことや改良方法を思いついた場合は、気軽にコメントして教えて欲しい。
\def\concat#1#2{#1 \, || \, #2}
記号の意味
この記事では次のような記号を、次のような意味で利用する。
| 記号 | 意味 |
|---|---|
| $Sign_A(B)$ | 秘密鍵$A$で$B$に署名 |
| $Extract_A(B)$ | 公開鍵$A$で署名されたデータ$B$を展開 |
| $Hash(A)$ | $A$のハッシュ値を計算 |
| $A := B $ | 変数$A$に$B$を代入 |
| $\concat{A}{B} $ | $A$と$B$を結合 |
| $A , \& , B$ | $A$と$B$の論理積 |
| $A = B$ | $A$と$B$が等しい |
| $A \ne B$ | $A$と$B$が等しくない |
| $A \stackrel{?}{=} B$ | $A$と$B$が等しいかどうかを検証 |
対応する秘密鍵$d$と公開鍵$e$があるとき、任意のデータ$A$について次のことが成り立つ。
Extract_e(Sign_d(A)) = A
これは、秘密鍵で署名したものを対応する公開鍵で展開した結果が元のデータに等しいことを意味している。また、次の式も成り立つ。
Sign_d(Extract_e(A)) \ne A
RSA署名などでは$Sign_d(Extract_e(A)) = A$が成り立つが、今回用いる電子署名はこのように、公開鍵を使って暗号化してから秘密鍵で復号することはできない署名アルゴリズムを用いる。
プロトコル
セットアップ
-
運営はカードとそれに対応するマスクを公開する。このマスクは$n$ビットで構成されていて、カードの種類と一対一に対応している。このマスクはSSRなど希少なカードほど1のビットが多く、Nなどありがちなカードほど0が多くなるようにしておく。カードを$K_1, K_2, \dots, K_i$とすると、マスクは次のようになる。
マスク 対応するカード $0000 \dots 1001$ $K_1$ $0010 \dots 0010$ $K_2$ $1110 \dots 0111$ $K_3$ $1011 \dots 1011$ $K_3$ $\vdots$ $\vdots$ $1111 \dots 0100$ $K_i$ このように、マスクとカードは一対一に対応している必要はなく、複数のマスクが同じカードに対応していてもよい。ただし、同じマスクが複数のカードに対応してはならない
-
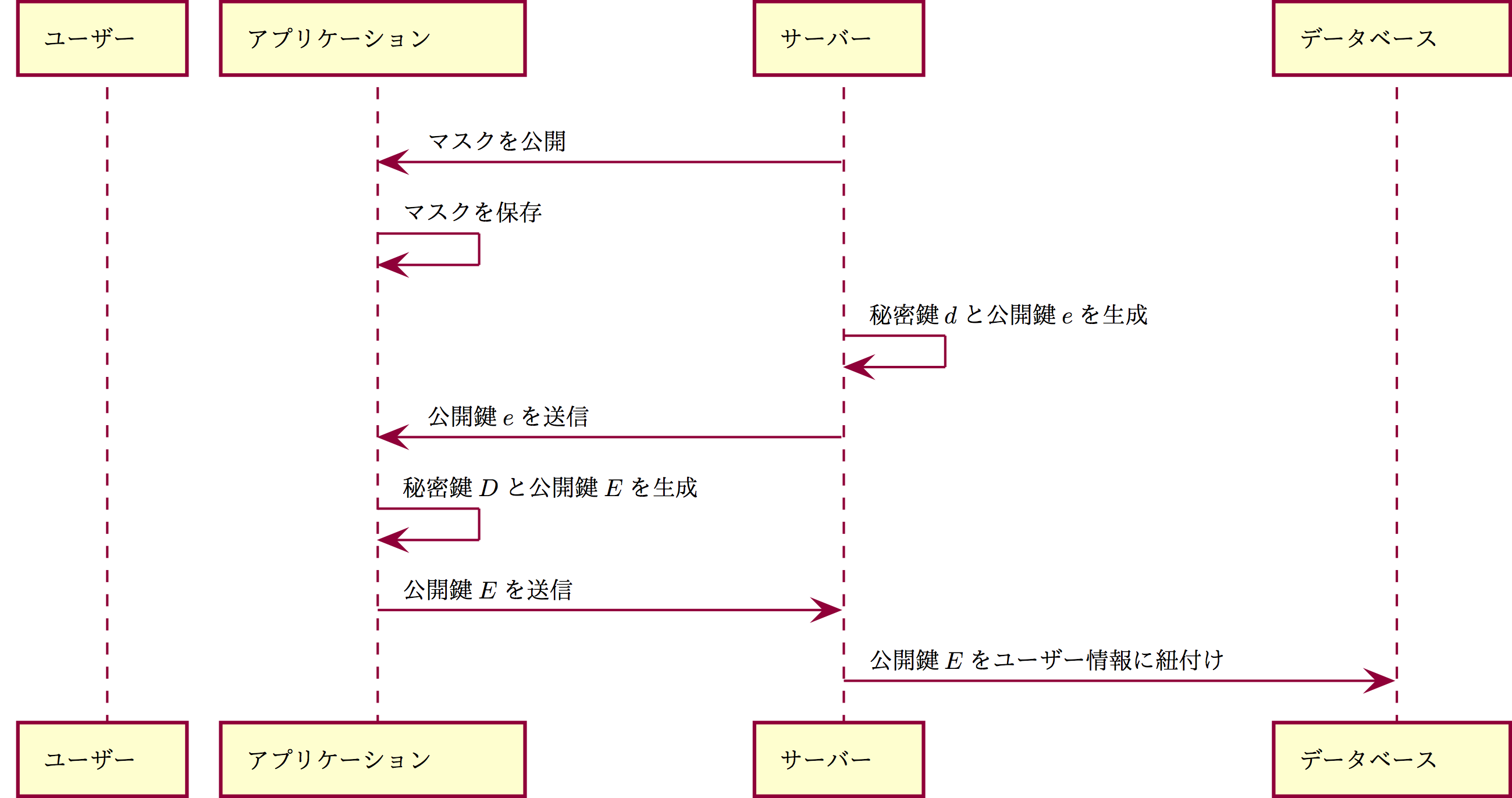
運営は署名の秘密鍵$d$と公開鍵$e$を用意し、公開鍵$e$を公開する
-
ユーザーにインストールされたガチャアプリケーションは、インストール時に署名の秘密鍵$D$と公開鍵$E$を生成し、公開鍵$E$を運営のサーバーへ送信する
-
運営のサーバーは、ユーザー情報と公開鍵$E$を関連付ける
またこのガチャではSSHのようにアプリケーションの秘密鍵$D$と公開鍵$E$を用いてユーザーの認証を行う。
シーケンス図
ガチャ
-
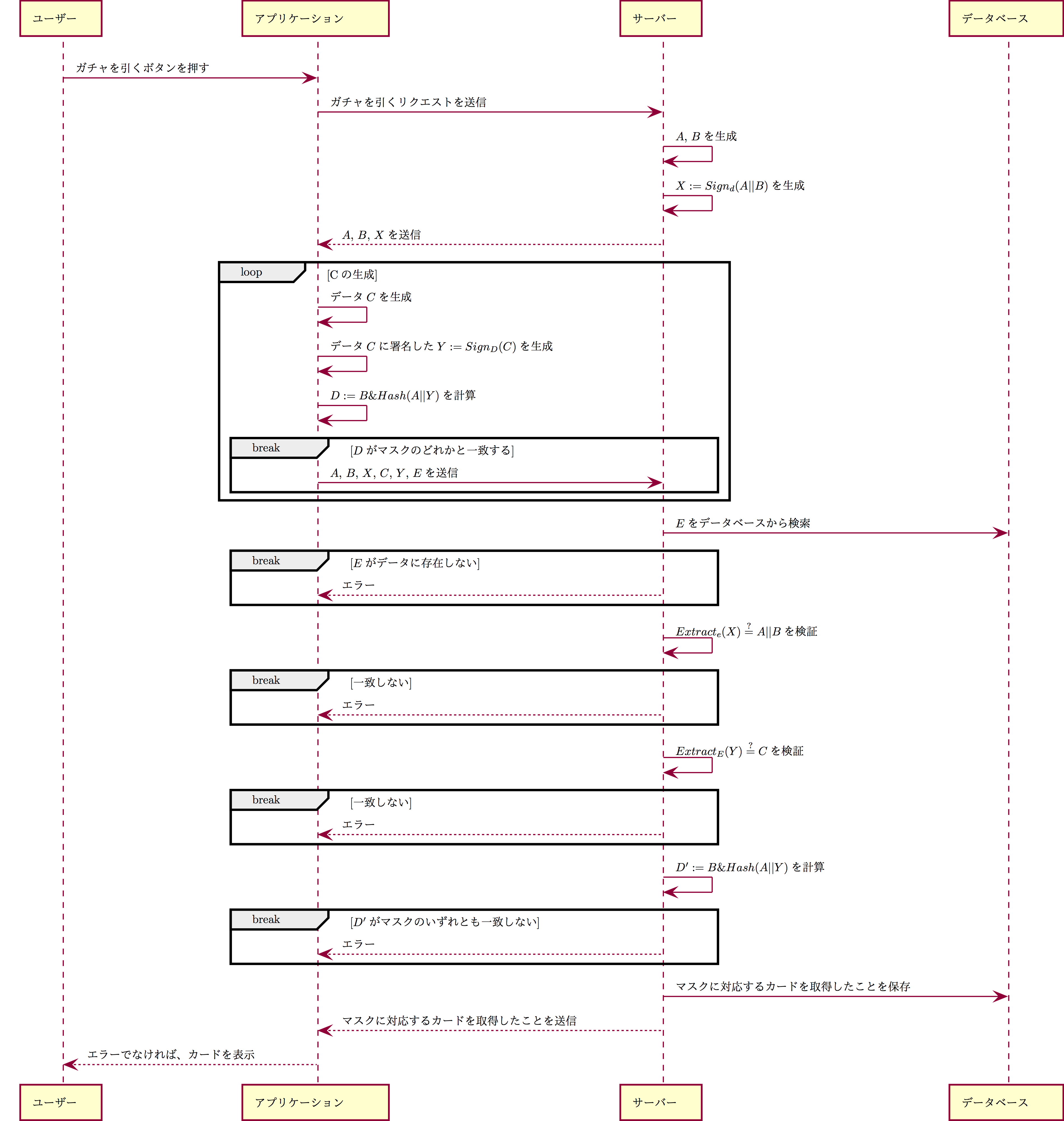
ユーザーがガチャを引こうとすると、アプリケーションがサーバーへそのことを通知する
-
サーバーは次のデータをアプリケーションへ送信する
-
無作為なデータ$A$
-
$n$ビットのデータ$B$
-
$A$と$B$を結合したデータにサーバーが鍵$d$で署名したデータ$X$
X := Sign_d(\concat{A}{B})
-
-
アプリケーションはデータ$C$をランダムに生成し、それに署名する
Y := Sign_D(C) -
アプリケーションはデータ$A$と$Y$を結合したデータのハッシュ値を計算し、$B$との論理積を計算しそれを$D$とする
D := B\, \& \, Hash(\concat{A}{Y}) -
アプリケーションは$D$と等しいマスクがあるかどうかによって、次の二つに分岐する
- もし$D$に等しいマスクがある場合は、次のデータをサーバーへ送信する
- データ$A$
- データ$B$
- データ$C$
- $A$と$B$を結合したデータにサーバーが秘密鍵$d$で署名した$X$
- データ$C$をアプリケーションが秘密鍵$D$で署名した$Y$
- アプリケーションの公開鍵$E$
- もし$D$に等しいマスクが一つもない場合は(3)からやりなおす
- もし$D$に等しいマスクがある場合は、次のデータをサーバーへ送信する
-
サーバーは次のことを検証する
-
$X$の署名を展開した結果と送信されたデータ$A$と$B$を結合した結果が一致するか
Extract_e(X) \stackrel{?}{=} \concat{A}{B} -
$Y$の署名を展開した結果と送信されたデータ$C$が一致するか
Extract_E(Y) \stackrel{?}{=} C
-
-
サーバーは送信された$Y$からアプリケーションと同様に$D'$を計算する
D' := B\, \&\, Hash(\concat{A}{Y}) -
サーバーは$D'$に等しいマスクに対応するカードを公開鍵$E$に対応するユーザーに与える
- もし$D'$に等しいマスクが一つもない場合はエラーを返す
シーケンス図
プロトコルの説明
サーバーはA, Bを結合した値に署名する必要はあるのか
この署名によって、データ$A$と$B$が確実にサーバーが用意したものであることを保証する。もし署名がない場合は悪意あるユーザーが、データ$A$を作った後で適当なデータ$C$を作り、狙ったマスクになるような$B$を作れてしまう。そこで公平性を保つために、悪意のあるユーザーにとって都合がいい$A$や$B$を生成されることを防ぐために$\concat{A}{B}$に署名する。
アプリケーションがデータCに署名する必要はあるのか
業者などが介入した場合、高性能なPCや専用ハードウェアを用いて$C$を高速に計算して、オークションなどで売買する可能性がある。それを防止するために、$C$を計算するたびにユーザーの秘密鍵$D$が必要となるように設計した。
業者が秘密鍵DとデータCの両方を売買する可能性はないのか
この可能性はある。ただし、このシステムがSSHと同じように秘密鍵と公開鍵によってユーザーを認証しているので、秘密鍵$D$と$C$を仮に売買によって入手したとしても、その$C$は秘密鍵$D$が対応するユーザーにしか使えない。従って、複数の業者からデータ$C$を購入しても同じユーザーで使うことはできない。あるユーザーが業者に計算してもらうと思うと、アカウントごと業者から買う必要があり、これはゲームバランスを崩すほど効率的な操作にはなり得ないという考えから、この方法に対しては対策していない。
ユーザーが業者に秘密鍵を教えてCなどを計算してもらう可能性はないのか
この可能性はあるが、ユーザーは業者などに自分のアカウントの秘密鍵を教えなければならない。また、このシステムは前提として秘密鍵を使ってSSHのようにログインするため、秘密鍵を教えた場合、アカウントにおける全ての操作を行えることになる。つまり業者とユーザーの間には、アカウントの全ての操作を許すような信頼関係が築かれていなければならない。このような信頼関係を業者との間に築くことは不可能であると考えているので、ユーザーが秘密鍵を業者に教えて計算してもらうというこの方法については特に対策していない。
ユーザーが一つのAを使ってDをひたすら計算し続ける可能性はないのか
このプロトコルをそのまま使うとそうなってしまうが、次のようにすれば回避できる。
- サーバーはデータ$A$の中に有効期限を示す時刻情報を入れる
- ユーザーから送信された$A$の中にある有効期限を検証し、過ぎていればエラーとする
もしユーザーがこの有効期限を偽造した、つまりは$A$を偽造したとしても、サーバーによって署名された$Sign_d(\concat{A}{B})$を偽造することはできない。従って、この方法を使うことで、データ$A$に有効期限を持たせることができ、結果としてユーザーが同じ$A$についてひたすら$D$を計算するという行為をある程度防止することができる1。
課金はどうするのか
通常のガチャには課金すると、無課金のガチャに比べてレアリティの高いカードが出現しやすくなる。このシステムでも次のようにすることで課金によるレアリティのコントロールを実装できる。
- 運営は課金した場合の課金マスクを公開する(課金金額により、いくつか用意する)
- ユーザーは課金すると、課金用の公開鍵を登録することができる
- アプリケーションは課金ガチャの場合は、課金マスクを用いて$D$を計算する
- サーバーは送信された公開鍵から課金情報を取得し、対応する課金マスクを用いて$D$を計算する
マスクのデータサイズが巨大になって、コンピュータのメモリに乗り切らなくなるのではないか
マスクは話を簡単にするため、カードとの1対多のテーブルとしたが、例えば「どの位置でもよいので、$1$の数が10個あるものは$K$」のような集合を記述してもよい。また、このシステムでは$C$を何度も計算することを前提としているので、マスクにヒットしない$D$が計算されることもある程度許容している。これらのことから、マスクのデータサイズを小さくすることが可能であると思われる。
ユーザーの間でハッシュ値や署名の計算能力に差が出るので、不公平ではないか
この指摘はもっともだが、このガチャシステムは運営とユーザーの間でカードの出現確率を秘密にできないという点が公平であるとしている。つまり、ユーザーと運営の間を透明にしているのであって、ユーザーとユーザーの間は平等に競争ができるという点で不公平かもしれない。一般的なガチャは、運営のサーバー内で確率の計算などが行われるため、ユーザーはサーバー内で起きている確率の計算が公表されている数値と同じなのかどうかを判断することはできない。一方で従来のガチャはユーザーが何をしてもサーバー内で起きている確率の計算に影響を与えないので、ユーザーとユーザーの間で競争することはできない。従ってユーザーとユーザーの間では競争ができないから公平であるとも言えるかもしれない。まとめると次のようになる。
- 従来のガチャ
- 運営とユーザーの間は不公平(不透明)だが、ユーザーとユーザーの間は公平(競争がない)
- 今回のガチャ
- 運営とユーザーの間は公平(透明)だが、ユーザーとユーザーの間は不公平(競争がある)