元論文
- Distributional Smoothing with Virtual Adversarial Training
- Virtual Adversarial Training: a Regularization Method for Supervised and Semi-supervised Learning
手法
Virtual Adversarial Trainingは各学習データ周辺における事後確率の分布を滑らかにすることでネットワークの汎化性能を向上させる手法です。
Virtual Adversarial TrainingはAdversarial Trainingから派生した手法で、学習データの正解ラベルから計算した損失の代わりに事後確率同士の距離から計算した損失を用いることでラベルなしのデータも学習に活用する事ができます。
損失
各学習データ周辺における事後確率の分布を滑らかにするために、データ$x$の事後確率$p(y|x)$と$x$に微小な摂動$r$を加えた$x+r$の事後確率$p(y|x+r)$を近づけるような損失を考えます。すなわち、距離関数$D$を用いて$D[p(y|x),p(y|x+r)]$を損失に加えて最小化します。$D$はKLダイバージェンスや二乗誤差などを用います。
全てのデータ点について、あらゆる方向に摂動させた点との事後確率の距離を小さくすればよいわけですが、入力データ空間が高次元の場合は現実的ではありません。そこで、$D[p(y|x),p(y|x+r)]$を最大にする$r_{vadv}$のみを用います。すなわち、入力データに対してネットワークが最も間違えやすい方向に摂動を加え、間違いが起きないようにネットワークの重みを更新します。そのような$p(y|x)$と$p(y|x+r_{vadv})$との距離$LDS$と定義します。
$$
\begin{eqnarray}
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
LDS(x) &\equiv& D[p(y|x),p(y|x+r_{vadv})] \
r_{vadv} &\equiv& \argmax_{r; ||r||_2 \leqq \epsilon} D[p(y|x),p(y|x+r)]
\end{eqnarray}
$$
$LDS(x)$はラベルありデータだけでなく、ラベルなしデータについても計算できることがポイントです。最終的な損失は下記のようになります。
$$
l(D_l) + \alpha \frac{1}{N_l+N_{ul}} \sum_{x \in D_l,D_{ul}}LDS(x)
$$
ここで、$D_l$,$D_{ul}$はそれぞれラベルありデータ、ラベルなしデータの集合です。$\epsilon$,$\alpha$はハイパパラメータ、$l(D_l)$はクロスエントロピーなど通常の教師あり学習で用いる損失です。
摂動の求め方
元論文では$r_{vadv}$の効率的な計算方法も紹介されています。
以下簡単のため$D[p(y|x),p(y|x+r)]$を$D(r,x)$と書きます。$||r||_2 \leqq \epsilon$
のもと$D(r,x)$を最大にする$r$を求めます。
$r=0$周りのテイラー展開を用いて$D(r,x)$を以下のように展開します。ここで、$D(r,x)$は$r$に関して二階微分可能であることを仮定しています。
$$
D(r,x) \approx D(0,x) + r^{\mathrm{T}} \left. \nabla_r D(r,x) \right|_{r=0} + \frac{1}{2} r^{\mathrm{T}} H(x) r
$$
ただし$H(x)$は以下で定義されるヘッシアンです。
$$
H(x) \equiv \left. \nabla \nabla_r D(r,x) \right|_{r=0}
$$
$D$は2つの事後確率の距離を表すので、$r=0$のときは2つの事後確率は等しくなり距離は0となります。
$$
D(0,x) = D[p(y|x),p(y|x)] = 0
$$
また距離は正の値を取るため$r=0$において最小値を取ることになります。すなわち$r=0$における勾配も0になります。
$$
r^{\mathrm{T}} \left. \nabla_r D(r,x) \right|_{r=0}=0
$$
よって$D(r,x)$は以下のように近似できます。
$$
D(r,x) \approx \frac{1}{2} r^{\mathrm{T}} H(x) r
$$
これはいわゆる二次形式であり、$r^{\mathrm{T}} H(x) r$を最大化する$r$は$H(x)$の最大固有値に対応する固有ベクトルとなりす。
最大固有値に対応する固有ベクトルはべき乗法を用いると簡単に求まります。今回はノルム1のランダムなベクトル$d^0$を初期値として
- $d^{k+1} \gets H(x)d^k$
- $d^{k+1} \gets d^{k+1} / ||d^{k+1}||$
を繰り返すことによって求めることができます。元論文ではこの反復回数をハイパパラメータ$Ip$としています。
上記のべき乗法の計算には$H(x)$が必要ですが直接計算するのは困難です。そこで差分法を用いて$H(x)d$を以下のように近似します。
$$
\begin{eqnarray}
H(x)d &\approx& \frac{\left. \nabla_r D(r,x) \right|_{r=\xi d} - \left. \nabla_r D(r,x) \right|_{r=0} }{\xi} \
&=& \frac{\left. \nabla_r D(r,x) \right|_{r=\xi d} }{\xi}
\end{eqnarray}
$$
ここで、再び$\left. \nabla_r D(r,x) \right|_{r=0}=0$を用いました。$\xi$はハイパパラメータです。右辺の係数$1/\xi$はノルム1に正規化するときに消えるのでべき乗法の計算のときは無視できます。このように直接ヘッセ行列を求めない手法はHessian Freeと呼ばれているようです。
べき乗法によって求まった$d$は$||d||_2=1$なので条件$||r||_2 \leqq \epsilon$に合うよう係数$\epsilon$をかけた$\epsilon d$を$r_{vadv}$とします。ここで$\epsilon$が大きいと近似の精度が悪くなる点には注意が必要です。
ハイパパラメータ
VATを用いた学習には4つのハイパパラメータ$\epsilon$, $\alpha$, $\xi$, $Ip$が存在します。
べき乗法の反復回数$Ip$については、元論文の実験で$Ip=1$で十分であることが確認されています。
損失関数のバランス係数$\alpha$については、筆者はすべての実験を$\alpha=1$で行ったと述べています。これは$\epsilon$が以下のようにバランス係数の役割も兼ねることができるためと考えられています。
$$
\begin{eqnarray}
LDS(x) &\approx& \frac{1}{2} r_{vadv}^{\mathrm{T}} H(x) r_{vadv}\
&=& \frac{1}{2} (\epsilon d)^{\mathrm{T}} H(x) (\epsilon d)\
&=& \frac{1}{2} \epsilon^2 \lambda_1(x)
\end{eqnarray}
$$
$\lambda_1(x)$は$H(x)$の最大固有値です。
$\epsilon$は学習用データとは別に用意したvalidationデータを用いて決定します。
差分法で$H(x)d$を求めるときの係数$\xi$については詳しく記述されていませんでした。
実験
学習時の挙動
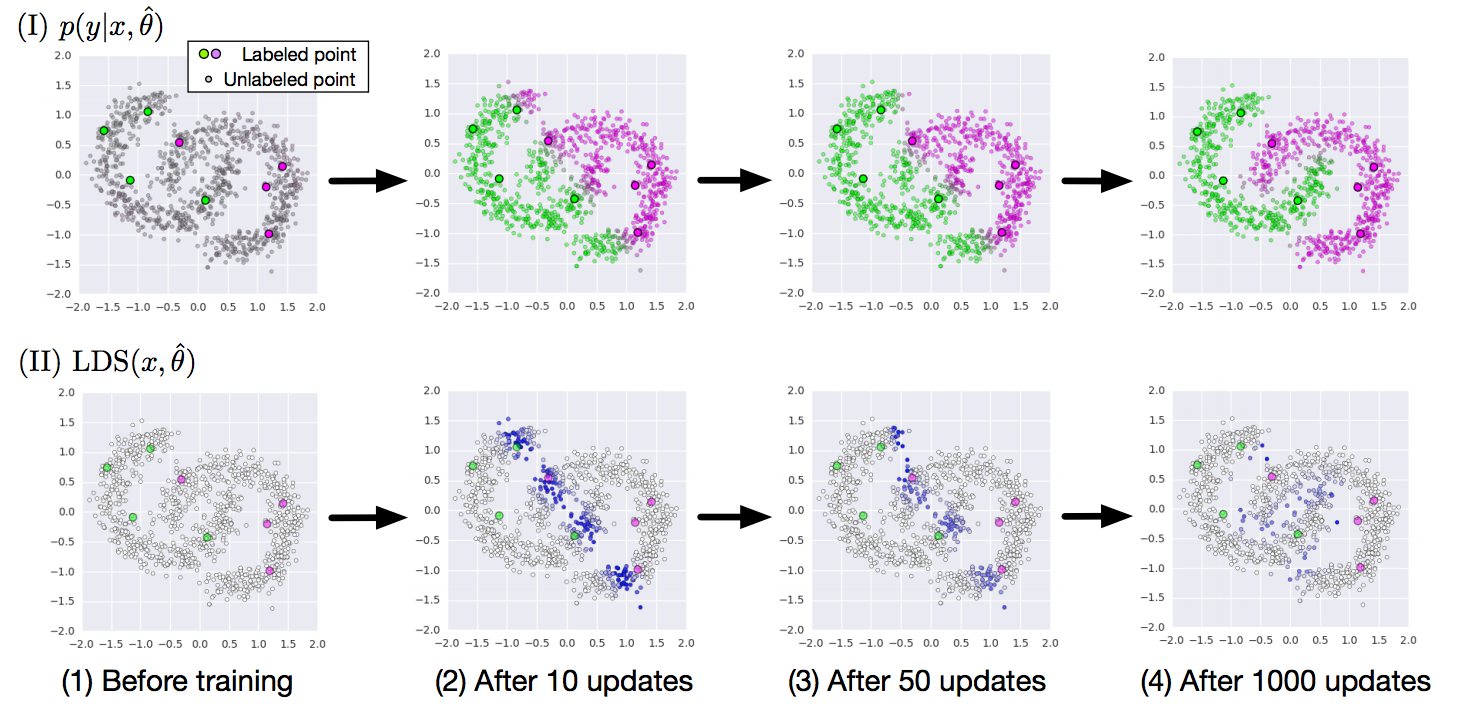 ([元論文](https://arxiv.org/abs/1704.03976)から転載)
上の図は二次元空間上の点の2クラス分類問題における学習の経過を示しています。
(I)では学習が進むに連れ灰色で示されたラベルなしデータが近いクラスタに分類されていく様子が、(II)では識別境界付近のデータ、すなわち誤識別の起こりやすいデータで$LDS(x)$が大きくなっていることがわかります。
([元論文](https://arxiv.org/abs/1704.03976)から転載)
上の図は二次元空間上の点の2クラス分類問題における学習の経過を示しています。
(I)では学習が進むに連れ灰色で示されたラベルなしデータが近いクラスタに分類されていく様子が、(II)では識別境界付近のデータ、すなわち誤識別の起こりやすいデータで$LDS(x)$が大きくなっていることがわかります。
実験結果
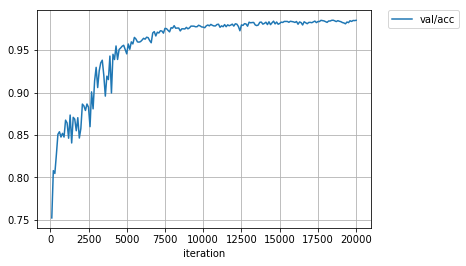
MNISTでラベルありデータ数を100、ラベルなしデータ数を59,900として半教師あり実験を行いました。半教師あり学習の論文ではよくある問題設定です。ちなみにデータ数100で教師あり学習すると認識率は70%程度です。
誤認識率(認識率)はおよそ1.6%(98.4%)前後に落ち着きました。論文の1.36%(98.64%)と比べて悪くない値だと思います。
下図は入力画像(左)に摂動を加えた画像Virtual Adversarial Example(右)の例です。違いをわかりやすくするため摂動をノルム10になるよう増幅しています。上から5が3に、9が5に、7が9に、3が5に見えます。
