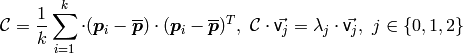PCL(Point Cloud Library)の公式チュートリアルをもとに点群(point clouds)における法線(normals)推定についてまとめたいと思います。
#法線推定はなぜ必要?
メッシュが張られていない点群データに対しては、局所部分(n近傍)での法線方向を、近似的にメッシュを推定していくことでその垂線として法線方向も推定していく必要があります。
CGでは、光源からの光の反射を正しく表したり、その他の視覚効果を作成するうえで貴重な情報となります。

#法線推定手法
法線推定には2パターン方法があります。
・Point cloudに対して先にメッシュ化を行い、できあがったメッシュの各面における垂直方向をサーフェス法線とする
・メッシュ化は行わず、Point Cloudの幾何構造から直接サーフェス法線を推定する
メッシュ化の方法によっては、法線が求められてないとできないものもあるため、点群から直接法線を推定するほうが多いかと思います。
###理論
法線推定手法にはいくつかあるみたいですが、最も単純な**「最小二乗法 (least-squares)により、局所的な点群(k近傍)に対して平面を当てはめることで、その平面をサーフェスとみなし、サーフェスの垂直方向を法線とする」**という手法を用います。
最小二乗法は以下のように定式化されます。
このCは、ある注目点の近傍における、点と中央点の距離が要素である共分散行列です。この共分散行列を主成分分析(PCA)で解いて固有ベクトル(主成分方向)を出すことで、第一主成分と第2主成分が「一番点が多い方向と2番目に点が多い方向=平面のx、y方向」とみなすことができるので、その平面の垂線が法線であると推定できます。
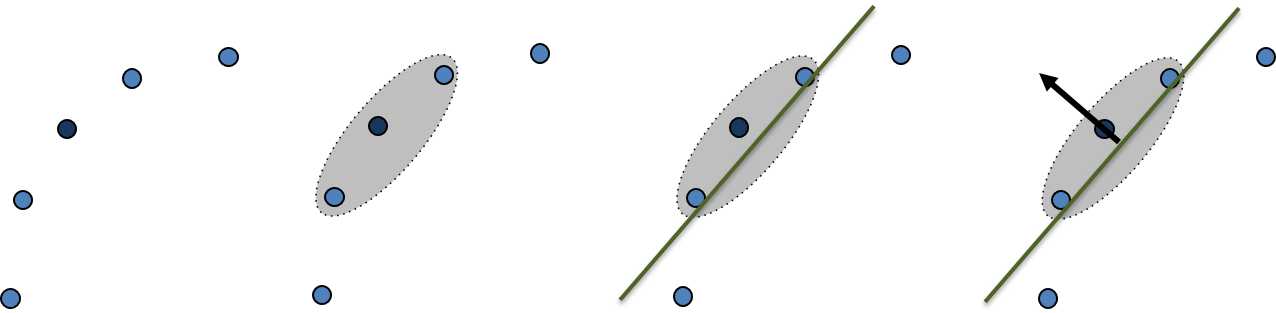
ただ、この方法だと平面方向をSVDで出しただけなので、どっちが表か裏かは毎回適当になり、PCAにより出してきた法線方向には正負のあいまい性が残ります。
PCLでこの問題を解決するには、ビューポイント(カメラ視点方向)に対して各法線が統一した方向になるように、カメラの方向と反対の裏側に向いている法線だけを表裏の反転(flip)を行います。
あるいは、spanning tree を用いて大域的な方向を求めることもできます。
###スケールの選択
既に述べられたように、サーフェス法線の推定は、注目点の近くの範囲に含まれていると推定した点だけについて行われます。この推定する近傍点の範囲をK最近傍(k-nearest neighborhood)といいますが、法線推定ではこの推定する近傍のスケールが、どの程度の値が最も良いのかを決める必要があります。
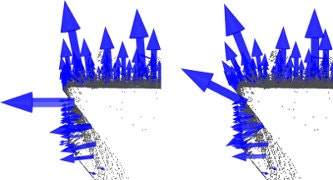
左が小さいスケール、右が大きいスケールのもので、矢印のあるほうが法線を、ヒートマップの方が曲率(curvature)を示しています。**小さいスケールの方が当然細かい局所的な法線を推定することになり計算コストもかかります。大きいスケールだと全体的な大きな法線はとらえるものの、エッジやノイズに敏感となります。**それぞれ、アプリケーションしだいで大きさを決めることになる、と結論づけられています。
具体的な値については述べられていませんが、半径r(radius)を用いる場合と一番近い順にk点用いる場合があります(MeshLabなんかでは後者を用いてた気がします)。