ｋ近傍法の原理とpythonでの実装

内容

・ｋ近傍法とは

・pythonでの実装

目標

・正しさより、イメージしやすさ重視での理論の説明

・可視化するために二次元データで実装

ｋ近傍法とは

ざっくりいうと・・・

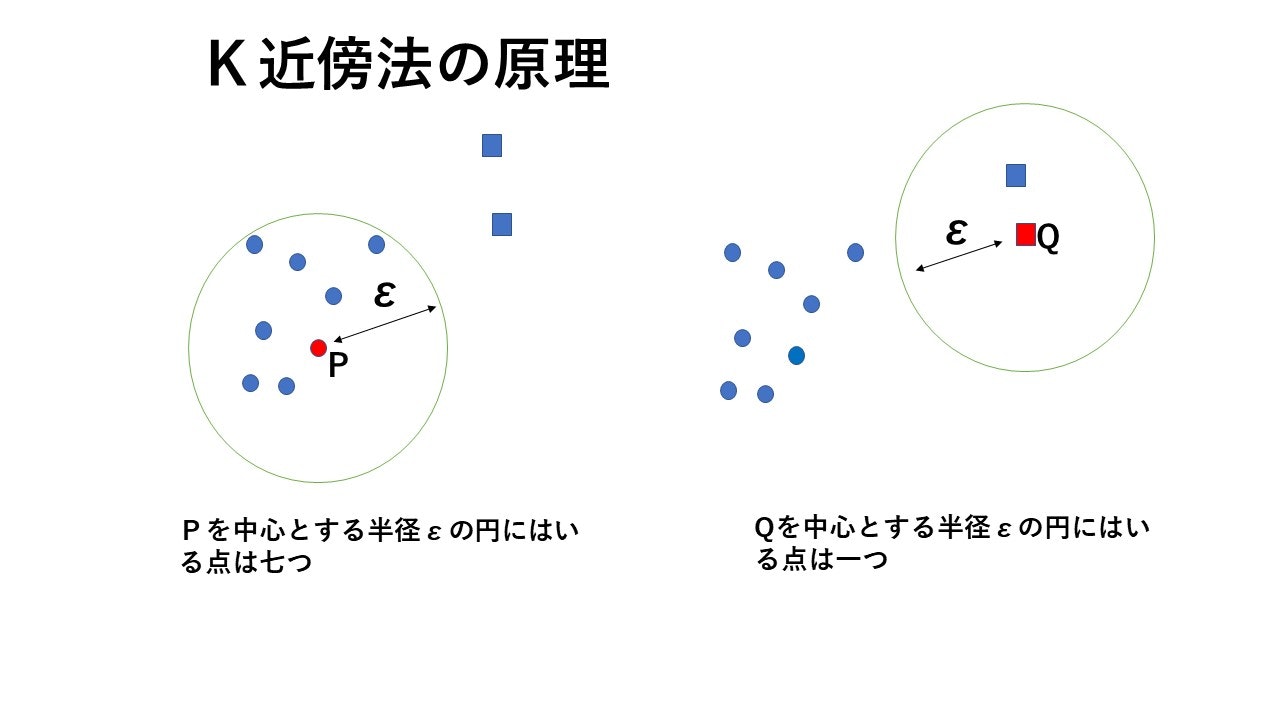
データの集まりのうち、異常度を調べたいデータをｐとする。

ｐを中心とする円を考える。円を少しずつ大きくしていき、円に含まれる点の数がｋ個になったらその時の半径をεとする。

これがｋ近傍法の基本的な考え方。

ｐが正常なデータの集まりから離れているとき、ｋは小さくなり、ｐの周りに正常なデータが多く存在するとき、ｋは大きくなる。

ｋを決めてデータを含むｐを中心とする円の半径の最小値εの大きさで異常度を判定してもよい←今回はこれ

局所外れ値や、多クラスなどの機械学習に使われるｋ近傍法の応用的な理論はもう少し複雑ですが、とりあえず簡単な理論で実装しましょう。

pythonでの実装

環境

・python3.6

・windows10

データの生成

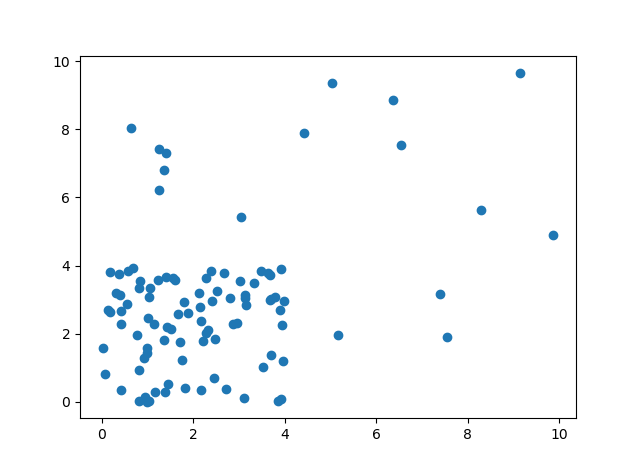
numpy　の乱数で二次元データを作成

このまとまりから外れているデータを識別したい。

先ほどの原理をそのままコードにする。

knn.py

class KNN2d:

    def knn2d(self, x, y, k):
        num = x.shape[0]
        ipsilon_list = []
        for j in range(num):
            l_list = [] #k番目のデータに対するその他のデータの距離
            for i in range(num):
                xl = x[i] - x[j]
                yl = y[i] - y[j]
                l2 = (xl) ** 2 + (yl) ** 2
                l = l2 ** 0.5
                l_list.append(l)
            l_li = np.array(l_list)
            l_li = np.sort(l_li)
            ipsilon_list.append(l_li[k])
        abnormals = np.array(ipsilon_list)

        return abnormals/10


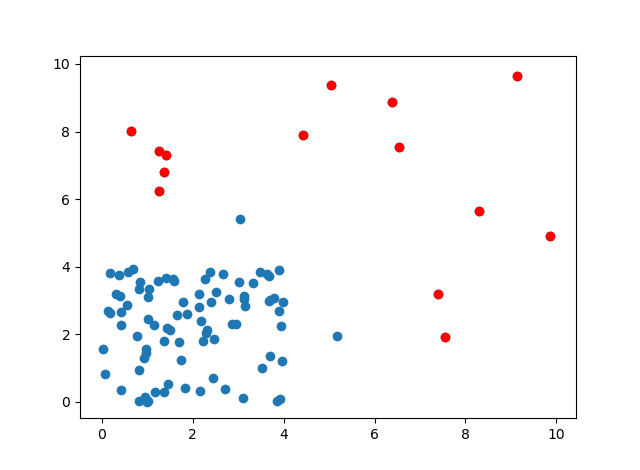
    def abnormal_decision(self, abnormals, treshold):
        result_list = []
        num = abnormals.shape[0]
        for i in range(num):
            abnormal = abnormals[i]
            if abnormal > treshold:
                result_list.append(i)
        return result_list

判定結果

離れたところにあるプロットをおおむね識別できた。

閾値εを手動で設定しないといけないなど、実用するには改良しないとだけど、イメージはつかめた。