"ROOT: Robust Orthogonalized Optimizer for Neural Network Training" という論文の紹介です。
この論文は、大規模言語モデル(LLM)の学習が不安定になりがちな問題を、
「最適化アルゴリズムそのものの設計」から解決しようとする研究です。
何が問題だったのか
近年、AdamW に代わる手法として Muon のような
行列構造を意識した最適化手法が登場しました。
しかし、これらには次のような弱点があります。
- 行列の形状(正方・縦長・横長)によって精度が大きく変わる
- 勾配に混じる極端なノイズに弱い
- 大規模化するほど学習が不安定になる
つまり、
LLM のように巨大で多様な構造を持つモデルでは、
既存の最適化手法では限界が見え始めている、という状況です。
ROOT の核心アイデア:Dual Robustness
ROOT の最大の特徴は、2つの頑丈さを同時に満たす設計にあります。
1. Algorithmic Robustness
Muon では、行列が正方でも長方形でも
同じ係数で直交化を行っていました。
ROOT ではこれを見直し、
- 行列サイズごとに
- 最適な係数を個別に計算
することで、どんな形の層でも高精度な更新を可能にします。
2. Optimization Robustness(ノイズに強い)
大規模学習では、勾配に
異常に大きな値(外れ値) が混じることがあります。
ROOT はこれを、
- 勾配を「本体」と「外れ値」に分けて考え
- Soft-Thresholding によって外れ値だけを抑制
することで対処します。
つまり、 ノイズに振り回されず、学習の方向性を保つ設計です。
ROOT を支える2つの技術
1. Adaptive Newton-Schulz Iteration(AdaNewton)
従来の Newton-Schulz 法は係数が固定で、
特定の行列サイズでは誤差が大きくなっていました。
ROOT では、
- 行列サイズごとに
- 直交化誤差が最小になる係数を学習
することで、この問題を解消しています。
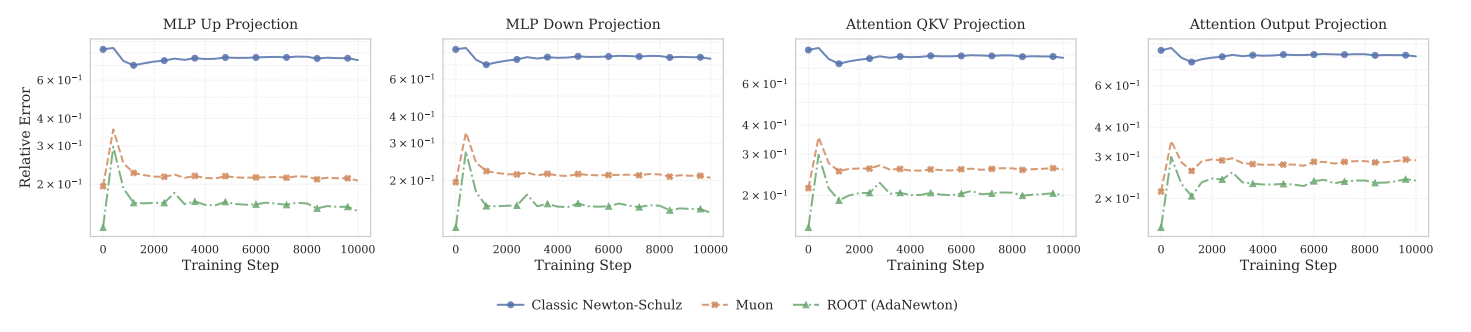
結果として、
直交化誤差は Muon 比で最大 100 倍以上削減されています。
2. Soft-Thresholding による近接最適化
Momentum 行列に対して L1 正則化由来の
Soft-Thresholding を適用することで、
- 外れ値は抑えつつ
- 有効な勾配方向は保持
する更新が可能になります。
実験結果から分かること
ROOT は以下の点で一貫して優れた結果を示しています。
- 学習の安定性:損失が発散しにくい
- 収束速度:より早く低損失に到達
- 汎化性能:下流タスクで高スコア
- 汎用性:LLM だけでなく Vision モデルでも有効
特に注目なのは、最後の点で、CIFAR-10 の ViT(Vision Transformer) 学習でも
Muon を大きく上回った点です。
まとめ
LLM の事前学習での発散が怖いので、ゆっくりでもよいから絶対に学習を壊したくない、という設計意図かと思います。
ViT はあくまでも「これにも一応使えるよー」くらいの温度感でしょう。
参考