アルゴリズム体操６

#Find Low or High Index

##説明
整数型のソートされた配列と、指定された要素(key)が位置する最も低いインデックス(low index)と高いインデックス(high index)を返す。もし、指定された要素がその配列にない場合は-1を返します。配列の長さは数百万単位で、多くの重複要素を許します。

##例
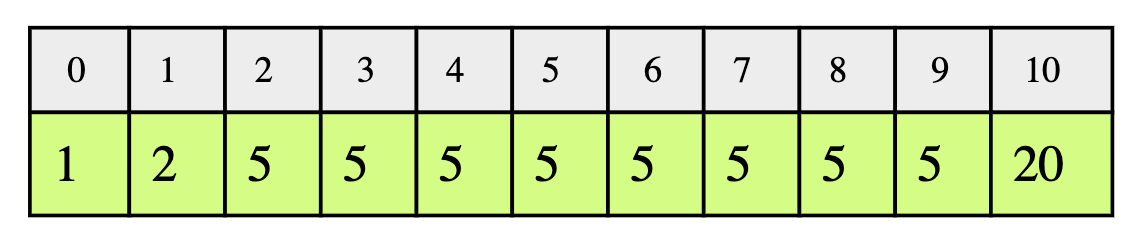
次の例では、low index と high index は次のようになります。

key：1　low = 0 および high = 0

key：2　low = 1 および high = 1

key：5　low = 2 および high = 9

key：20　low = 10 および high = 10

##ヒント
Binary Search

##解説
###Runtime Complexity
Binary Search を使用しているため、実行時間はO（logn）です。
###Memory Complexity
定数のO（1）です。 追加のメモリは使用ましせん。 ただし、Binary Search が再帰的に実装された場合、
関数呼び出しによるスタックで暗黙的にO（logn）、メモリが使用されることに注意してください。
ただし、ここでは反復(Iteration)に焦点を当てます。

###思考
配列サイズは数百万単位であるため、ソートされた配列をlow indexおよび high indexでO(n)で
線形スキャンすることは非常に非効率的です。 代わりに、少し修正を加えてBinary Searchを使用して、
特定のkey の low indexと high index を見つけます。

low index を見つけるためのアルゴリズムを見てみましょう。

1. すべてのステップで、low index と high index の間の配列を検討します。また、low index と high index の中間の mid index を計算します。

1. mid の要素が key 以上の場合は、high = mid - 1になります。もし、mid の要素が keyと同じの場合でも、そのindexが最低のindexとは限らないことに注意します。

3. mid の要素がkey より小さい場合、配列は昇順なので　keyは 始めの 0 からmid　までの範囲に存在しません。よって、mid + 1以降にある可能性があります。low = mid + 1 になります。 4. low が high よりも大きい場合、反復を終了し、low は key の最初の出現を指します。low の要素が key と一致しない場合、-1を返します。

　＊high index を見つける場合も上記のプロセスとほぼ同じです。以下に実装コードがあります。

##実装

findLowHigh.java

import java.util.List;

public class findLowHigh{

    public int binary_search(List<Integer> arr, int low, int high, int key, boolean search_low){

        while(low <= high) {
            int mid = low + (high - low) / 2;

            if (search_low) {
                if (arr.get(mid) >= key) { // Search the left half for the next
                    high = mid - 1;
                }
                else { // Search the right half for the next
                    low = mid + 1;
                }
            }
            else {
                if (arr.get(mid) <= key) { // Search the left half for the next
                    low = mid + 1;
                }
                else { // Search the right half for the next
                    high = mid - 1;
                }
            }
        }

        if (search_low) {
            if (low == - 1) {
                return low;
            }
            else if (low < arr.size() && arr.get(low) == key) {
                return low;
            }
        } else {
            if (high == -1) {
                return high;
            }
            else if (high < arr.size() && arr.get(high) == key) {
                return high;
            }
        }

        return -1;
    }

    public int find_low_index(List<Integer> arr, int key) {
        return binary_search(arr, 0, arr.size() - 1, key, true);
    }

    public int find_high_index(List<Integer> arr, int key) {
        return binary_search(arr, 0, arr.size() - 1, key, false);
    }
}

Main.java

import java.util.Arrays;
import java.util.List;

public class Main {

    public static void main(String[] args) {

        findLowHigh algorithm = new findLowHigh();

        List<Integer> array = Arrays.asList(1,1,1,2,2,2,2,2,3,3,3,4,4,4,4,5,5,5,6,6,6,6,6,6);
        int key = 5;
        int low = algorithm.find_low_index(array, key);
        int high = algorithm.find_high_index(array, key);
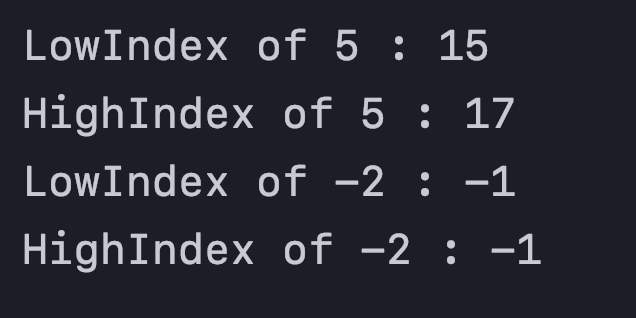
        System.out.println("LowIndex of " + key + " : "+low);
        System.out.println("HighIndex of " + key + " : "+high);

        key = -2;
        low = algorithm.find_low_index(array, key);
        high = algorithm.find_high_index(array, key);
        System.out.println("LowIndex of " + key + " : "+low);
        System.out.println("HighIndex of " + key + " : "+high);
    }
}

###Output