【かんたん解説付き】深層ボルツマンマシンをPythonでスクラッチ実装する①

この記事は Wacul Advent Calendar 18日目の記事です。

#自己紹介
　株式会社WACULの解析チームで１年前から働いています。
　python歴：3週間くらい

#やること
　pythonの練習　&　確率的なディープラーニングの勉強目的メインで、深層ボルツマンマシンをスクラッチ実装してみます。理論面は全て以下の本の中にある内容です。

『深層学習 (機械学習プロフェッショナルシリーズ)』 岡谷 貴之 (著)
『深層学習 Deep Learning』(監修:人工知能学会)

　本記事ではまず準備として制限ボルツマンマシンを実装します。次回、制限ボルツマンマシンを積み上げて深層ボルツマンマシンを構築します。

#ボルツマンマシンの簡単な説明
　確率分布は、端的には「値の集合に対して、それが得られる確率密度(確率質量)を対応させる関数」なので、全体としては「値の集合を生成する背後のメカニズム」として捉えることができます。これを生成モデルと呼びます。
　生成モデルを構築できれば、変数間の関係を把握したり期待値を計算できたりと、応用の幅が広がります。
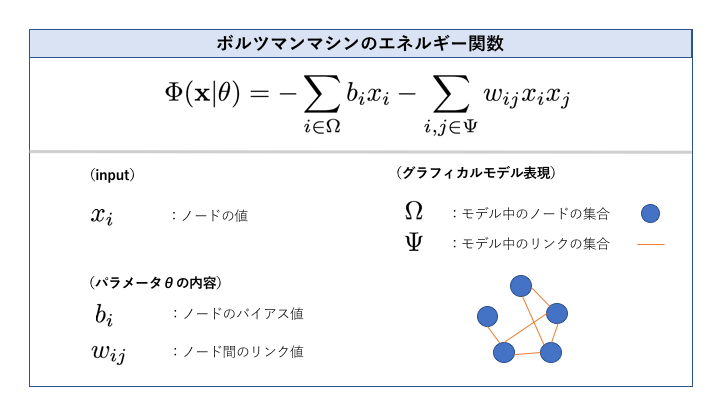
　今回取り上げるボルツマンマシンとは、ボルツマン分布を用いて確率密度を計算する生成モデルです。具体的な確率密度は、下記で定義されるエネルギー関数（Φ）にマイナスをかけたものの指数関数をとった上で値を規格化したものになります。（[0,1]の閉区間に収めるために定数を掛ける）　
　エネルギー関数はノードのバイアスとリンクそれぞれの重み付き線形和になっています。

#可視変数と隠れ変数
　可視変数とは直接観測可能な変数、隠れ変数とは観測できない変数のことです。隠れ変数を導入することで、ボルツマンマシンの表現力は向上します。
　尚、隠れ変数を含むモデルの場合は、最尤推定時の目的関数に隠れ変数に関して周辺化した可視変数のみの分布を用います。

#制限ボルツマンマシン
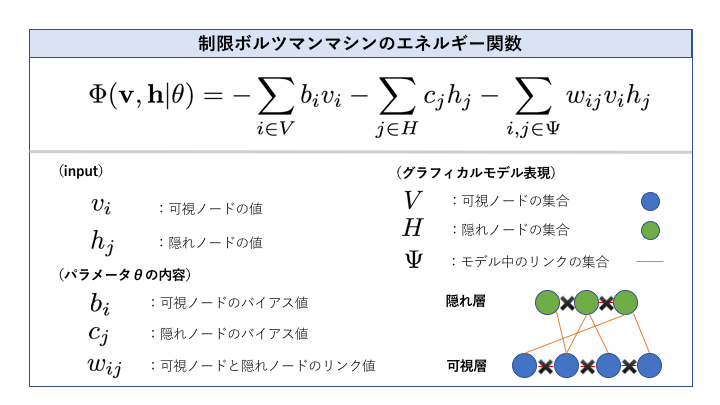
　制限ボルツマンマシンは、一般のボルツマンマシンに隠れ変数を導入した上で一定の制約を加えることにより、パラメータ推定を簡単にしたモデルです。その制約とは
①　可視ノード間にリンクがない
②　隠れノード間にリンクがない
の2つです。
　この２つの条件から、制限ボルツマンマシンは可視ノードのみからなる「可視層」と隠れノードのみからなる「隠れ層」の二つの層を持ち、異なる層の間でのみリンクを持つモデルとして表現されることになります。

　このことは片方の層に対して片方の層が条件付き独立であることを意味するので、
・可視層の全ノードの現在の期待値からと隠れ層の全ノードのサンプル群を得る
・隠れ層の全ノードのサンプル群から隠れ層の全ノードの期待値を近似する
・隠れ層の全ノードの期待値から可視層の全ノードのサンプル群を得る
・可視層の全ノードのサンプル群から可視層の全ノードの期待値を近似する
というプロセスを回すことができます。
　この計算は比較的簡単で、しかもそれぞれの層のサンプルを一気に得ることができるという利点があります。制限ボルツマンマシンの制限は、モデルの表現力と引き換えにこの恩恵を受ける為のものと言えます。

#制限ボルツマンマシンの学習
　モデルの形を決めたら、次にやることはパラメータの学習です。
　制限ボルツマンマシンのパラメータ学習は、対数尤度関数の最大化を目的としてオーソドックスに勾配（上昇）法を用います。
　勾配上昇法とは、目的関数の値が増える方向にパラメータを少しずつ更新していくプロセスを繰り返しながら関数の最大化を狙う方法で、今回の目的関数はデータの尤度（全学習サンプルの同時分布）です。これを最大化するために、目的関数をターゲットのパラメータで微分して勾配を求めます。
　勾配を計算する際に可視層・隠れ層の期待値が必要になりますが、これは直接計算が困難なので、ギブスサンプリングを用いてサンプルを実際に生成し平均をとることで近似します。この時、上記の制限ボルツマンマシンのもつ「層間の条件付き独立性」の恩恵により簡便に計算が実行できます。

学習は、大きく見ると以下のようなプロセスを踏みます。

⚫️ パラメータをランダムに初期化


⚫️ 以下繰り返し ----------------------------------------------

　　　　①　　　　現在のパラメータの値を用いて、可視層と隠れ層を交互にサンプリング

　　　　②　　　　①を用いて可視層、隠れ層の各ノードの期待値を計算

  ③　　　　②を用いて可視層のバイアス、隠れ層のバイアス、リンクそれぞれの勾配（微分）を計算
　　　　
　　　　④　　　　③を用いてパラメータを更新
  ---------------------------------------------------------

#制限ボルツマンマシンのPython実装
サンプリング時にpersistent contrastive divergence法を使っています。
処理効率を考えてないので収束判定は省略しています。

RBMクラスの実装

from typing import List
Input = List[int]

def sigmoid(z):
    return 1/(1+np.exp(-z))


class RBM:
    learningRate = 0.005
    sample_num = 100
    
    #Vnは可視ノード数、Hnは隠れノード数
    def __init__(self , Vn : int , Hn : int):
        self.Vn = Vn
        self.Hn = Hn
        self.bias_v = np.array(np.random.rand(Vn)) #ランダムに初期化
        self.bias_h = np.array(np.random.rand(Hn)) #ランダムに初期化
        self.link  = np.array(np.random.rand(Vn,Hn)) #ランダムに初期化
        
        self.hidden_value = []
        
    def train(self, data_for_learning , iteration_times):
        for iteration_times in range(iteration_times):
            
            # samples_vh　はv * h のサンプル
            samples_h =[]
            samples_v = []
            samples_vh = np.zeros((self.Vn,self.Hn))
            
            messege_in_sampling = 0
            sigmoid_belief = 0
        
            #　①　　現在のパラメータの値を用いて、可視層と隠れ層を交互にサンプリング
            for index in range(RBM.sample_num):
                
                current_v = data_for_learning[0]
                current_h = np.zeros(self.Hn)
                                
                ## 隠れ層をサンプリング
                for j in  range(self.Hn) :  
                    messege_in_sampling = self.bias_h[j] + sum(list(map(lambda i: current_v[i] * self.link[i][j]  , range(self.Vn))))                
                    
                    sigmoid_belief = 1/(1+ np.exp(-1 * messege_in_sampling))
                    
                    r = np.random.rand(1)
                    
                    if sigmoid_belief > r[0]  :
                        current_h[j] = 1
                    else : 
                        current_h[j] = 0
                
                samples_h.append(current_h)
                  
                ## 可視層をサンプリング
                for i in range(self.Vn):
                    messege_in_sampling = self.bias_v[i] + sum(list(map(lambda j: current_h[j] * self.link[i][j]  , range(self.Hn))))                
                    
                    sigmoid_belief = 1/(1+ np.exp(-1 * messege_in_sampling))
                    
                    r = np.random.rand(1)
                    if sigmoid_belief > r[0]  :
                        current_v[i] = 1
                    else : 
                        current_v[i] = 0
                                        
                samples_v.append(current_v)  
                
                ## 可視層　✖️ 隠れ層　をサンプリング
                z = itertools.product(current_v,current_h)
                
                product = []
                for element in z:
                    product.append(element)
                    
                current_vh = (np.array(list(map(lambda x : x[0] * x[1] ,product))) ) .reshape(self.Vn,self.Hn)
                    
                samples_vh += current_vh
            
            # ②　可視層、隠れ層の各ノードの期待値を計算
            E_V  = np.sum(np.array(samples_v),axis=0) / RBM.sample_num
            E_H = np.sum(np.array(samples_h),axis=0) / RBM.sample_num
            E_VH = samples_vh / RBM.sample_num

            # ③　可視層のバイアス、隠れ層のバイアス、リンクそれぞれの勾配（微分）を計算
            ## 可視層のバイアスの微分
            gradient_v = sum(np.array(data_for_learning)) / len(data_for_learning) - E_V
                
            ## 隠れ層のバイアスの微分
            gradient_h = []
            for j in range(len(self.bias_h)):
                gradient_h_1 = []
                sigmoid_beliefs_h_1 = []

                for n in range(len(data_for_learning)):
                    messege_h_1 = self.bias_h[j] + sum(list(map(lambda i: data_for_learning[n][i] * self.link[i][j]  , range(self.Vn))))
                    sigmoid_belief_h_1 = 1/(1+ np.exp(-1 * messege_h_1))
                    sigmoid_beliefs_h_1.append(sigmoid_belief_h_1)
                
                gradient_h_1 = sum(sigmoid_beliefs_h_1) / len(data_for_learning)      
                gradient_h_2 = E_H[j]

                gradient_h_j =  gradient_h_1 +  gradient_h_2
                gradient_h.append(gradient_h_j)

            ## リンクの微分
            gradient_vh = []
            for i in range(len(self.bias_v)):
                for j in range(len(self.bias_h)):
                    gradient_vh_1 = []
                    sigmoid_beliefs_vh_1 = []

                    for n in range(len(data_for_learning)):
                        messege_vh = self.bias_h[j] + sum(list(map(lambda i: data_for_learning[n][i] * self.link[i][j]  , range(self.Vn))))
                        sigmoid_belief_vh_1 = 1/(1+ np.exp(-1 * messege_vh))
                        sigmoid_beliefs_vh_1.append(sigmoid_belief_vh_1 * data_for_learning[n][i])

                    gradient_vh_1 = sum(sigmoid_beliefs_vh_1) / len(data_for_learning)      
                    gradient_vh_2 = E_VH[i][j]

                    gradient_vh_ij =  gradient_vh_1 +  gradient_vh_2

                    gradient_vh.append(gradient_vh_ij)

            # ④  ③を用いてパラメータを更新
            self.bias_v += RBM.learningRate *  np.array(gradient_v)
            self.bias_h += RBM.learningRate *  np.array(gradient_h)
            self.link +=  RBM.learningRate *  np.array(gradient_vh).reshape(self.Vn,self.Hn)            

    def energy(self,input : Input) -> float:
        # 可視層のエネルギー
        energy_v = sum(list(map(lambda i : self.bias_v[i] * input[i]  , range(self.Vn))))
        
        # 隠れ層のエネルギー
        ## 隠れ層の推定値
        hidden_layer = self.getHiddenValue(input)
                
        energy_h = sum(list(map(lambda j : self.bias_h[j] * hidden_layer[j]  , range(self.Hn))))
        
        # linkのエネルギー
        accumlator = []        
        for i in range(self.Vn):
            for j in range(self.Hn):
                accumlator.append(input[i]*hidden_layer[j] * self.link[i][j])
                
        energy_vh = sum(accumlator)       
                
        energy = -1 * (energy_v + energy_h + energy_vh)
        
        return energy
    
    def estimate(self,input:Input) -> float:            
    
        #エネルギー関数を計算
        energy = self.energy(input)
        
        #分配関数を計算
        all_patterns = list(itertools.product(range(0,2), repeat=self.Vn))
        partition = sum(list(map(lambda x: np.exp(-1 *self.energy(list(x))) , all_patterns)))
            
        return  np.exp(-1*  energy ) / partition
            
    def getHiddenValue(self,input:Input) :
        
        hidden_layer = np.zeros(self.Hn)
            
        for j in  range(self.Hn) :  
            messege_in_sampling = self.bias_h[j] + sum(list(map(lambda i: input[i] * self.link[i][j]  , range(self.Vn))))                
            sigmoid_belief = 1/(1+ np.exp(-1 * messege_in_sampling))
            
            r = np.random.rand(1)
            if sigmoid_belief > r[0]:
                hidden_layer[j] = 1
            else : 
                hidden_layer[j] = 0
                
        self.hidden_value = hidden_layer
        
        return hidden_layer

実行例

# 構築
visible_nord = 3
hidden_nord = 4
rbm = RBM(visible_nord,hidden_nord)

#　学習データ作成
training_data = np.array(list(map(lambda x : np.random.randint(0,2) , range(0,300)))).reshape(100,3)

#　パラメータ学習
rbm.train(training_data,10)
print(rbm.link)

input  = [1,0,1]

# 隠れ層の値取得
rbm.getHiddenValue(input)

# エネルギー関数の出力
rbm.energy(input)

# 確率密度の出力
rbm.estimate()

一応動くようですが合ってるのかは不明。。。
とりあえず先に進むことにします。

#次回
次回はこの制限ボルツマンマシンを組みわせて深層ボルツマンマシンを構成します。
層が深くなると学習が急激に難しくなるため、先に制限ボルツマンマシンを用いて事前学習しておくことでパラメータの良い初期値を得ておき、これを使って全体のモデルを微調整するというストーリーになります。