【かんたん解説付き】深層ボルツマンマシンをPythonでスクラッチ実装する②

この記事は Wacul Advent Calendar 2016 最終日の記事です。

前回

　準備として、制限ボルツマンマシンを実装しました。
　今回はこの制限ボルツマンマシンを「積み上げて」深層ボルツマンマシンを構成します。

【かんたん解説付き】深層ボルツマンマシンをPythonでスクラッチ実装する①
http://qiita.com/yutaitatsu/items/a9478841357b10789514

深層ボルツマンマシンとは

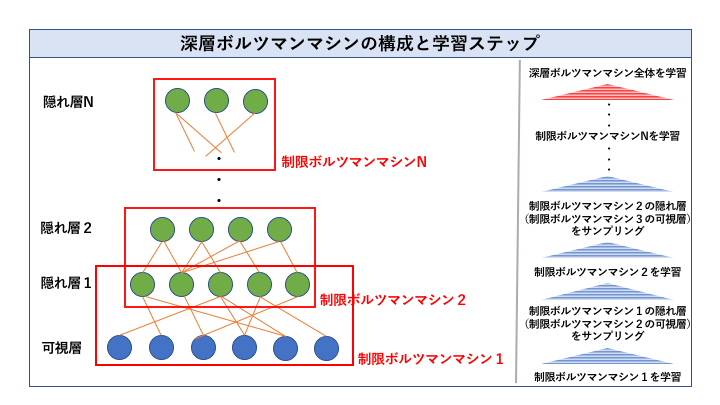
　前回解説したボルツマンマシン（隠れ層あり）の一種です。全体として一つの生成モデルを表現します。一番下に可視層を持ち、その上に隠れ層を積み上げた構成をしています。
　
　深層ボルツマンマシンは一般的な隠れ層ありボルツマンマシンの一種なので、そのまま勾配法で学習することができます。しかし、層が深くなればなるほど推定すべきパラメータの数が増え、局所解に落ちるリスクが高くなります。

学習の工夫

　そこで、***それぞれの層は条件付き独立（同じ層のノード間にはリンクがない）***とします。今回紹介する深層ボルツマンマシン学習の最大のトリックはここにあります。なぜそうするのかというと、下から順に、層２つずつを制限ボルツマンマシンとみなすためです。下から２層ずつのペアを制限ボルツマンマシンと見做し、ペアごとに事前学習することでパラメータの良い初期値を得ることを狙うわけです。具体的には以下のステップを踏みます。

【事前学習のステップ】

①　まず可視層を含む（一番下の）制限ボルツマンマシンを学習する
②　①で学習した制限ボルツマンマシンにおいて、「可視層から隠れ層の条件付分布」を用いて隠れ層の値をサンプリングする
③　②で得たサンプルを、次の（下から２番目の）制限ボルツマンマシンの可視層の入力とみなし、学習する
（以下繰り返し）

　パラメータの良い初期値を得た後は、オーソドックスに勾配法で再学習します。但し、層が深いと期待値の計算コストが爆発的に増大するため、現実的な時間で解を得るために近似法が必要となります。

近似手法

　近似は、勾配を計算する際、現在のパラメータの下での期待値を計算するために必要になります。このあたりは前回の制限ボルツマンマシンと同じです。
　
　分布の期待値を近似するための手法は大きく分けて二つあります。
　一つは前回の制限ボルツマンマシン学習時に利用した「ギプスサンプリング」のようなサンプリング法で、もう一つは今回用いる「平均場近似」のような変分法です。今回は、この両方の手法を利用します。

　サンプリング法と変分法の違いは、前者が「ターゲットとなる分布そのものから実際にサンプルを大量に発生させ、その平均をとることで期待値を近似する」のに対して、後者が「期待値が解析的に（簡単に）計算できる分布の中でターゲット分布に一番近いものを代わりに用いる」という点です。前者はサンプルが無限に得られれば、真の期待値に値が収束することを保証しているのに対して、後者はそうでない点に注意が必要です。

　具体的には、サンプリング手法はマルコフ連鎖モンテカルロ法（MCMC）を、変分法は混合ガウス分布などの分布群に対してターゲット分布とのKLdivergenceを最小にするパラメータを推定し、これを用いるということをします。

深層ボルツマンマシンの利用法

　深層ボツルマンマシンはそのまま生成モデルとして利用するの他に「オートエンコーダー」としての利用方法があります。
　これはどういうことかというと、各隠れ層が可視層の次元削減と見なせるということです。つまり、隠れ層の値は、可視層の各ノードが持つ情報の本質を保存しつつ次元を下げた特徴量とみなすことが可能です。
　従って、深層ボルツマンマシンは、確定的なニューラルネットワークや他のオーソドックスな機械学習手法を適用するためのデータの前処理として応用することができます。

実装例

　※　深層ボルツマンマシンのパラメータは全て、それを構成する制限ボルツマンマシンのパラメータとして保持しています
　※　ギブスサプリング、及び平均場近似の期待値計算を利用しています
　※　事後学習時のエネルギー関数はリンクの値のみを用い、バイアスは省略しています

深層ボルツマンマシンの実装

from typing import List
from itertools import chain
Layer = List[int]
Input = List[int]

from pprint import pprint

def sigmoid(z):
    return 1/(1+np.exp(-z))

def get_array_from_structure(base_array, structure):
    result = []
    current_index = 0 
    for index in range(len(structure)):
        accumlator = []
        if index == 0:
            accumlator = base_array[0:structure[current_index]]
        else:
            accumlator = base_array[current_index: current_index + structure[index]]

        current_index += structure[index]
        result.append(accumlator)
    
    return result

class DeepBolzmannMachine:
    learningRate = 0.05
    sample_num = 100
    
    def __init__(self,layer_structure:Layer):
        # Visible層から順にペアにして、RBMのリストを生成
        
        ## 層構造
        self.layer_structure = layer_structure
        self.layer_num = len(layer_structure)
        
        ## ペア作る
        self.pairs = []
        for i in range(len(layer_structure) -1):
            self.pairs.append((layer_structure[i],layer_structure[i+1]))
        
        ##  ペアごとにRBMを生成
        self.rbms = []
        for pair in self.pairs:
            rbm = RBM(pair[0],pair[1])
            self.rbms.append(rbm)
            
        self.link_structure = list(map(lambda x :x[0] *x[1], self.pairs))
 
    def preTrain(self,initaial_data_for_learning:Input, sample_num : int):

        current_learning_data = []

        ##RBM一つ一つ初期値を計算
        for rbm_index in range(len(self.rbms)):            
            # レイヤーが最下層の場合（Visible　対 Hidden の場合）
            if rbm_index == 0:
                self.rbms[rbm_index].train(initaial_data_for_learning,100)
                
                for i in range(sample_num):
                    hidden_value = self.rbms[rbm_index].getHiddenValue(initaial_data_for_learning[i])
                    current_learning_data.append(hidden_value)
            
            # レイヤーが最下層でない場合（Hidden　対 Hidden の場合）
            else:
                # 入力データで学習する
                self.rbms[rbm_index].train(current_learning_data,100)
                
                # 次のRBM用のデータを作る
                data_for_learning = []
                for i in range(sample_num):
                    hidden_value = self.rbms[rbm_index].getHiddenValue(current_learning_data[i])
                    data_for_learning.append(hidden_value)
                    
                current_learning_data = data_for_learning
               

    # 事前学習で得たパラメータを初期値に、勾配上昇法で更新する
    # 対数尤度関数のリンクパラメータによる微分の第１項を平均場近似、第２項をContrastive Divergenceで求める
    def train(self, data_for_learning:Input, iteration_times:int):
        samples = []
        for iteration_times in range(iteration_times):            
            # サンプル入力１つに対する、各隠れ層・各ノードの期待値を平均場近似で計算　【注: リンクだけを更新し、バイアスは更新しない】
            ## 期待値の中間データ(mean_field)は三次元配列として保持 （s番目サンプル / r層 / j番目の変数の期待値）
            sample_length = len(data_for_learning)
            max_node_num = max(self.layer_structure)
            
            mean_field = np.zeros((sample_length, self.layer_num, max_node_num))
            for s in range(sample_length):
                for r in range(self.layer_num):
                    if r == 0:
                        pass
                    elif r == 1:
                        for j in range(self.rbms[0].Hn):
                            first_paragraph = sum(map(lambda i : self.rbms[0].link[i][j] * data_for_learning[s][i] , range(self.rbms[0].Vn)))
                            second_paragraph = sum(map(lambda k : self.rbms[1].link[j][k] * mean_field[s][1][k] , range(self.rbms[1].Hn)))
                            
                            mean_field[s][1][j]  =  sigmoid(first_paragraph + second_paragraph)
                            
                    elif r == self.layer_num - 1:
                        for j in range(self.rbms[r -1].Hn):
                            mean_field[s][r][j]  =  sigmoid(sum(map(lambda k : self.rbms[r-1].link[k][j] * mean_field[s][r-1][k]  , range(self.rbms[r-2].Hn))))
                
                    else :
                        for j in range(self.rbms[r -1].Hn):
                            mean_field[s][r][j]  =  sigmoid(sum(map(lambda k : self.rbms[r -1].link[k][j] * mean_field[s][r-2][k]  , range(self.rbms[r - 2].Hn))) + sum(map(lambda l : self.rbms[r].link[j][l] * mean_field[s][r+1][l] , range(self.rbms[r].Hn))))

            # リンクの勾配の第一項を計算する
            gradient_1 = []
            
            for r in range(len(self.rbms)):
                gradient_1_element = []
                if r == 0:
                    for i in range(self.rbms[0].Vn):
                        for j in range(self.rbms[0].Hn):
                            gradient_1_element.append((sum(map(lambda s : data_for_learning[s][i]  * mean_field[s][1][j]  , range(sample_length)))) / sample_length)
                        
                else:
                    for i in range(self.rbms[r].Vn):
                        for j in range(self.rbms[r].Hn):
                            gradient_1_element.append((sum(map(lambda s : mean_field[s][r][i]  * mean_field[s][r+1][j]  , range(sample_length)))) / sample_length)
                
                gradient_1.append(gradient_1_element)
            
            # リンクの勾配の第二項を計算する
            
            ## サンプリングする
            new_samples = []    
            for s in range(DeepBolzmannMachine.sample_num):
                sample = []
                ##sampleの値を初期化
                for layer in self.layer_structure:
                    accumlator = []
                    for i in range(layer):
                        accumlator.append(np.empty)
                    sample.append(accumlator)
            
                ##サンプリングするための初期値をセット（この時、勾配上昇ループの２回目以降は、前回のサンプルを使う）
                initial_randoms = []
                if iteration_times == 0:
                    for layer in self.layer_structure:
                        accumlator = []
                        for i in range(layer):
                            accumlator.append(np.random.rand(1)[0])
                        initial_randoms.append(accumlator)
                else:
                    initial_randoms = samples[s]

                ##１つのサンプル（各ノードの値）を推定する
                sigmoid_belief = []
                for layer_index in range(len(self.layer_structure)):
                    for node_index in range(self.layer_structure[layer_index]):
                        #### そのノードに結合している全てのノードからのメッセージを使ってsigmoid beliefを計算する
                        if layer_index == 0:
                            sigmoid_belief = sigmoid(sum(map(lambda j : initial_randoms[1][j] * self.rbms[0].link[node_index][j]  , range(self.layer_structure[1]))))
            
                        elif layer_index == self.layer_num -1:
                            sigmoid_belief = sigmoid(sum(map(lambda j : initial_randoms[self.layer_num - 2][j] * self.rbms[self.layer_num -2].link[j][node_index]  , range(self.layer_structure[self.layer_num -2]))))
            
                        else :
                            belief_downstair = sum(map(lambda j : initial_randoms[layer_index - 1][j] * self.rbms[layer_index -1].link[j][node_index]  , range(self.layer_structure[layer_index -1])))
                            belief_upstair = sum(map(lambda j : initial_randoms[layer_index + 1][j] * self.rbms[layer_index].link[node_index][j]  , range(self.layer_structure[layer_index + 1])))
                            sigmoid_belief = sigmoid(belief_upstair  + belief_downstair)
            
                        #### 乱数を生成
                        r = np.random.rand(1)[0]
                    
                        #### sigmoid beliefが乱数より大きかったら１、小さかったら０をセット
                        if sigmoid_belief > r :
                            sample[layer_index][node_index] = 1
                        else: 
                            sample[layer_index][node_index] = 0
            
                #サンプルを加える
                new_samples.append(sample)
                
            #前回の勾配更新時のサンプルを捨てて今回のサンプルに置き換える
            samples = new_samples
        
            #サンプルから勾配第二項を近似する
            gradient_2 = []
            for r in range(len(self.rbms)):
                gradient_2_element = []
                if r == 0:
                    for i in range(self.rbms[0].Vn):
                        for j in range(self.rbms[0].Hn):
                            gradient_2_element.append(sum(map(lambda m : samples[m][0][i] * samples[m][1][j], range(DeepBolzmannMachine.sample_num))) / DeepBolzmannMachine.sample_num)
                else :
                    for i in range(self.rbms[r].Vn):
                        for j in range(self.rbms[r].Hn):
                            gradient_2_element.append(sum(map(lambda m : samples[m][r][i] * samples[m][r+1][j], range(DeepBolzmannMachine.sample_num))) / DeepBolzmannMachine.sample_num)
                
                gradient_2.append(gradient_2_element)
            
            
            #勾配を計算する
            gradient_1_flatten = np.array(list(chain.from_iterable(gradient_1)))
            gradient_2_flatten = np.array(list(chain.from_iterable(gradient_2)))
            
            gradient_flatten = gradient_1_flatten + gradient_2_flatten            
            gradient = get_array_from_structure(gradient_flatten, self.link_structure)
            
            #パラメータを勾配で更新    
            for rbm_index in range(len(self.rbms)):
                self.rbms[rbm_index].link +=  DeepBolzmannMachine.learningRate *  gradient[rbm_index].reshape((self.rbms[rbm_index].Vn,self.rbms[rbm_index].Hn))

実行例

# 可視層から順に、ノード数が5、４、３、２の4層ネットワーク
layer_structure = [5,4,3,2]

# 期待値計算時にサンプリングするサンプル数
sample_num = 100

# ボルツマンマシンのインスタンス化
dbm = DeepBolzmannMachine(layer_structure)

# 適当な学習データ作る
data_for_learning = np.random.rand(100,layer_structure[0])

# 事前学習
dbm.preTrain(data_for_learning,sample_num)

# 事後学習
dbm.train(data_for_learning,sample_num)

おわり

というわけで実装してみました。

確率的なディープラーニングは、確定的なニューラルネットワークのディープラーニングほどは浸透していないようですが、個人的には***「事象を、その不確かさをを含めて把握する」***ベイズ的な考え方のメリットは大きいと思うので、こっちがデファクトスタンダードになればいいなーと思っています。

今年もあと僅かとなりました。
みなさま、良い年末を...