はじめに
研究で脳波(EEG)や脳磁図(MEG)データの解析をおこなう際、PCAやICAを用いて脳活動の成分を分解し、次元削減した結果を特徴量に解析をおこなうことになりました。
数学的な背景は正直よくわからないけど、とりあえず実装ベースで時系列データのPCAとICAについて備忘録としてまとめました。
*後々数学的な背景も追加できればと思います。
主成分分析(PCA)と独立成分分析(ICA)
PCAとは
Wikipedia より、
主成分分析(しゅせいぶんぶんせき、英: principal component analysis; PCA)は、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法。データの次元を削減するために用いられる。
主成分を与える変換は、第一主成分の分散を最大化し、続く主成分はそれまでに決定した主成分と直交するという拘束条件の下で分散を最大化するようにして選ばれる。
つまり、
データが正規分布に従うと仮定できる時、分散の大きい成分から順に直行方向に軸をとる手法
基底が直行しているため、アウトプットはお互い無相関なデータになる(線形的な関係は無いが、非線形的な関係はあるかもしれない)
ICAとは
Wikipedia より、
独立成分分析(どくりつせいぶんぶんせき、英: independent component analysis、ICA)は、多変量の信号を複数の加法的な成分に分離するための計算手法である。各成分は、ガウス的でない信号で相互に統計的独立なものを想定する。これはブラインド信号分離の特殊な場合である。
つまり、
データが統計的に独立で正規分布に従わないと仮定できる時、独立性が最大となる方向に軸をとる手法
アウトプットは正規分布に従わない独立したデータになる(線形的な関係も非線形的な関係もない)
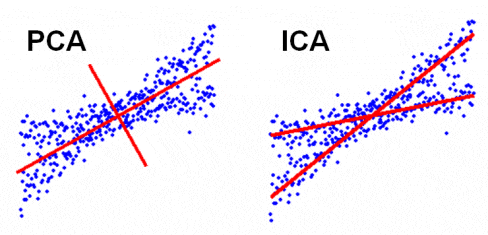
PCAとICAの違い(イメージ)
PCAの実装
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
X = input_data #400(データ数)×300(時系列)データ
# PCAの実行
pca = PCA(n_components=20, random_state=0)#20個の基底(コンポネント)を作る
feature = pca.fit_transform(X)
PCA_comp = pca.components_ #基底行列
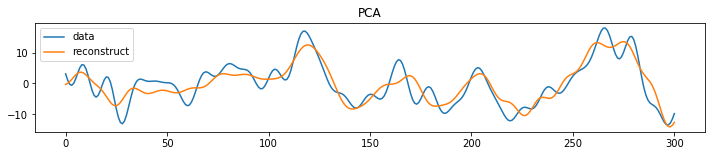
# 0番目のデータを20個のコンポネントを用いて復元
plt.figure(figsize = (12, 2))
plt.plot(X[0], label="data")#0番目のデータ
plt.plot(np.dot(feature[0], PCA_comp).T, label="reconstruct")#復元した0番目のデータ
plt.legend()
ICAの実装
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
X = input_data #400(データ数)×300(時系列)データ
# ICAの実行
ICA = FastICA(n_components=20, random_state=0)#20個の基底(コンポネント)を作る
X_transformed = ICA.fit_transform(X)
A_ = ICA.mixing_.T #混合行列
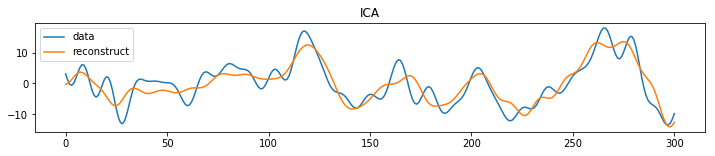
# 0番目のデータを20個のコンポネントを用いて復元
plt.figure(figsize = (12, 2))
plt.plot(X[0], label="data")#0番目のデータ
plt.plot(np.dot(X_transformed[0], A_), label="reconstruct")#復元した0番目のデータ
plt.legend()
おわりに
今回PCAとICAについて備忘録としてまとめました。
とりあえず実装できたからいいかな〜と言った感じですが、今後のためにもっと理論的な知識を付けなくては...と思っています。
NMF(非負行列因子分解)についても追記できたらと思います。