はじめに
星の明るさを伝えるために、
私たちは二つのものさしを愛用してきました。
flux と magnitude。
線形と対数。
頭では理解している。
……けれど、直感的に引き出せるかと問われれば、答えに詰まるかもしれません。
この二つの世界を自在に行き来できることは、
星のかすかな表情を、見逃さずに捉える力になるでしょう。
この記事では、
fluxとmagnitude、
この二つの関係を同じグラフに重ねて、可視化していきます。
本記事の実装コードはこちら(Google Colab)からもご覧いただけます。
fluxとmagnitudeの変換式
星の明るさを測るとき、
光の強さ(flux)と等級(magnitude)は、次の式で結ばれています。
m = -2.5 \log_{10}(F) + \text{zero_point}
逆に、
F = 10^{-0.4(m - \text{zero_point})}
と変換することもできます。
また、本記事では誤差の扱いを中心にしていませんが、
実際の測光データ解析では、誤差の変換が必要になる場面も多くあります。
そのため、コードには汎用性を考慮して、誤差も扱える形にしてあります。
ここで、誤差伝搬による変換後の誤差について、簡単に触れておきます。
- magnitudeに誤差 $\sigma_m$ があるとき、fluxの誤差 $\sigma_F$:
\sigma_F = \left| \frac{dF}{dm} \right| \sigma_m = 0.4 \ln(10) \times F \times \sigma_m
- fluxに誤差 $\sigma_F$ があるとき、magnitudeの誤差 $\sigma_m$:
\sigma_m = \left| \frac{dm}{dF} \right| \sigma_F = \frac{2.5}{\ln(10)} \times \frac{\sigma_F}{F}
Pythonで変換関数を作る
実際に、Pythonでこの変換をコードにしてみます。
ここでは、誤差の扱いがテーマではないため、単純に2軸表示に特化した方法を紹介します。
共通コード(関数定義とダミーデータ)
import numpy as np
import matplotlib.pyplot as plt
# 変換関数
def create_mag_flux_funcs(zero_point=0.0):
def mag_to_flux(mag, mag_err=None):
flux = 10**(-0.4 * (mag - zero_point))
if mag_err is not None:
flux_err = 0.4 * np.log(10) * flux * mag_err
return flux, flux_err
return flux
def flux_to_mag(flux, flux_err=None):
flux_safe = np.clip(flux, 1e-12, np.inf) # 0以下にならないように小さな値にクリップ
mag = -2.5 * np.log10(flux_safe) + zero_point
if flux_err is not None:
mag_err = (2.5 / np.log(10)) * (flux_err / flux)
return mag, mag_err
return mag
return mag_to_flux, flux_to_mag
# ダミーデータ
np.random.seed(0)
time = np.linspace(0, 5, 100)
true_mag = 13 + 0.5 * np.sin(2 * np.pi * time / 5)
mag_noise = true_mag + np.random.normal(0, 0.05, size=time.shape)
mag_to_flux, flux_to_mag = create_mag_flux_funcs(zero_point=13.0)
flux = mag_to_flux(mag_noise)
これで、mag_to_flux、flux_to_magの両方を簡単に呼び出せます。
なお、flux_to_mag()内では、
fluxがゼロまたは負になると、$\log_{10}$(flux) の計算で発散が生じます。
通常のデータ変換では問題になりにくいですが、
secondary_axisは軸目盛りのために幅広い値域で関数を呼び出すため、
不適切な値が入る可能性があります。
このエラーを防ぐため、fluxの下限値を十分小さな正の値(ここでは $10^{-12}$)にクリップしています。
プロット例1:magnitudeを主軸にして可視化
共通コードで作成したデータを使って、
magnitudeを左軸に、fluxを右軸に表示します。
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(time, mag_noise, label='Magnitude', color='blue')
ax.set_ylabel('Magnitude', color='blue')
ax.invert_yaxis()
secax = ax.secondary_yaxis('right', functions=(mag_to_flux, flux_to_mag))
secax.set_ylabel('Flux (arb. units)', color='red')
ax.set_xlabel('Time')
ax.grid(True)
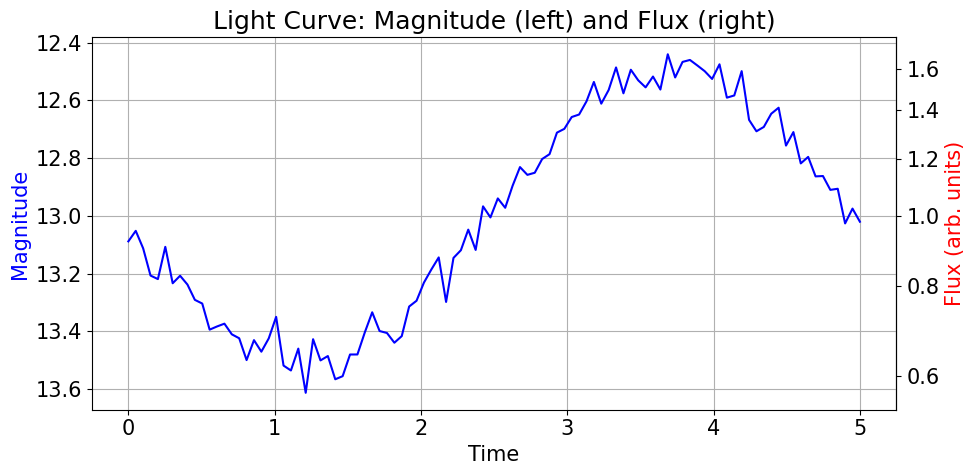
plt.title('Light Curve: Magnitude (left) and Flux (right)')
plt.tight_layout()
plt.show()
Magnitudeが13を基準にした時のFluxを右軸に表示しています。
プロット例2:fluxを主軸にして可視化
同様に、fluxを左軸に、magnitudeを右軸に表示します。
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(time, flux, label='Flux', color='red')
ax.set_ylabel('Flux (arb. units)', color='red')
secax = ax.secondary_yaxis('right', functions=(flux_to_mag, mag_to_flux))
secax.set_ylabel('Magnitude', color='blue')
secax.invert_yaxis()
ax.set_xlabel('Time')
ax.grid(True)
plt.title('Light Curve: Flux (left) and Magnitude (right)')
plt.tight_layout()
plt.show()
おわりに
私たちが観測する光は、
空の明るさも、大気の揺らぎも、観測装置の震えさえも——
あらゆるものを飲み込んで届きます。
それらすべてが、光という共通のラベルに溶け込み、
数式を介してfluxやmagnitudeへと言語化されます。
けれど。
私たちは、その数式の向こうにある「星の表情」を、
本当に感じ取れているでしょうか。
光をどう受け取り、どう読み取るか。
無数の選択の中から、確かなものを掬い取ること。
それが、星に「意味」を与えるのだと、
以前書いた この記事 が教えてくれました。
数式でつながっている。
でも、心でつながるには、もう一歩の想像力がいる。
可視化を通じて、
遠い灯火の知らなかった顔に気づけたとき——
それは、筆を上げるときかもしれません。