[初心者]CODE 〜コードから見たコンピュータのからくり〜 ②

はじめに

• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ①

からの続きです。

前編をまだ読んでいない方は、ぜひそちらを読んでから読むことをおすすめします。
（その方が内容が頭に入ってきやすいと思います。）

【シリーズ】

• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ①
• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ②←←←　本記事
• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ③・・・（現在執筆中）
• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ④・・・（現在執筆中）

②から読む方へ

簡単に概要を述べておくと、本シリーズは「CODE コードから見たコンピュータのからくり」という本を読んだまとめ記事となっています。

こちらの本が初心者の方に向けて非常にわかりやすくコンピュータの仕組みについてまとめてあったので、自分の復習も兼ねて記事にまとめることにしました。

またあくまで「書籍のまとめ」であるため、だらだらと文章にするのではなく、

• 「要点だけを掻い摘んで箇条書きで書いていく」

という形式を取っており、一部の方には少し読みづらい部分もあるかもしれませんが、ご容赦いただけると幸いです。

ただ内容についてはできる限り視座を下げて書いたつもりなので、基本的には誰にでもわかるようになっています。

初学者の方にもかなりとっつきやすい内容となっていますので、最後まで読んでいただけると嬉しいです。
（LGTMも押していただけるとなおありがたいです🙇‍♂️🙇‍♂️）

対象読者

• コンピュータの歴史に興味ある方
• コンピュータの仕組みについて理解したい人

目次

①

章	タイトル	備考
	はじめに
	対象読者
0.	イントロダクション	本書の概要を説明。全体像をつかめます。
1.	親友	モールスコードを例にコードについて基本的な説明。
2.	コードと組み合わせ	コードの個数の規則性から数学の組み合わせ論との関係性について説明。
3.	点字とバイナリコード	点字を用いてバイナリコードの仕組みについて説明。
4.	懐中電灯の解剖学	懐中電灯を用いて電気回路の基本的な仕組みについて説明。電気について軽く復習できます。
5.	角を回ってみる	双方向に情報を伝達する仕組みを懐中電灯の電気回路を用いて作成。またその際にボトルネックとなる点についても言及。
6.	電信とリレー	現在のコンピュータの基礎となっている「電信」と「リレー」について説明。

②

章	タイトル	備考
7.	私たちの10個の数字	位取り記数法について簡単に説明。
8.	10に代わるもの	2進数とビットについて説明。
9.	ちょびっとずつビットで	情報をビット単位で伝えることについて説明。ビットが情報の基本単位としていかに便利かということが理解できます。
10.	論理とスイッチ	ここからがメイン部分。まずは論理学とプール代数について説明。その後、プール代数と電気回路の一体化を猫の真偽テストを通して学んでいく
11.	ゲート	論理ゲートについて説明。4つの基本論理ゲートを中心に学んでいく
12.	2進数加算器	論理ゲートを組み合わせることで算術計算を自動で実行させることができる機械を作る。ここは現代コンピュータの基礎となっている部分でもあるので重要。
13.	でも引き算はどうする？	引き算を通してコンピュータが負の数をどのように扱っているのか？を見ていく

③

現在執筆中です。

④

現在執筆中です。

7. 私たちの10個の数字

数という抽象的な概念

• 数は非常に抽象的な概念

• 数字は数という抽象概念を表現した単なる記号（コード）の一種であって、例えば５という概念は私たちがよく見慣れたアラビア数字の5と表してもいいし、あるいは漢数字の五やローマ数字のⅤと表してもいい

数の歴史

• 数という概念は元々、人、所有物などや商取引で物を数えるために発明された。というのも人が自分の感覚だけで様々なものを扱っていると不都合が生じてきたからである。

• そもそも人間は一度に捉えられる物の数は5つが限界であり、例えば5個だろうが6個だろうが一眼見ただけでは区別がつかない。

• そうした感覚だけで物の取引をしていると当然不都合が生じてくる。つまり実際数えてみたら差がある物でも数という概念がなかったら同じものとして捉えてしまうのである

• そのため昔の人には数という概念の発明は非常に画期的なものとなった。数の発明により人間は自分の感覚を遥かに超えるものを扱えるようになり、それは利害共有を元とする社会において非常に重要なこととなった。

• しかしそうなってくると、今度はその数をどう表現するのか？といったことが問題となってきた。

• この問題は結構難しく、昔の人々は様々な表現方法を発明した。石を用いた表現方法や単純に骨や木片に切り傷を入れたりなど...

• そうした紆余曲折の末たどり着いたのが**「記数法」**という考え方である。

• これはアラビア数字やローマ数字、漢数字などのように適当な文字や記号と一定の規則を用いて数を表現する方法である。

• そしてこの中で現在最も一般的に用いられているのが**「アラビア数字」**である。

アラビア数字

• アラビア数字は一般的な記数法とは違った特徴を持っている

• まずアラビア数字は**「位取り記数法」**と呼ばれ、数字がどの位置にあるかによって異なる量となる。つまり、アラビア数字にとって「数字がどこにあるか」が非常に重要となる

• またそれまでは存在していた10を表すための記号が存在せず、代わりに今まで存在していなかった0という記号と概念を作った。

• この0という概念と記号がアラビア数字をアラビア数字たるものとしている。

• • 具体的にはアラビア数字は今までの記数法と違い、掛け算や割り算などのような位取りしない記数法では不便な演算が非常に簡単になった。
  • またあるいは、数字の区別も容易になった
  • アラビア数字の細かな説明についてはこちらをぜひ参考にしてください。

• この位取り記数法の最も良い点は、この仕組みにより各種の演算が楽になるといったことよりも、たとえ10に基づかない記数法であってもうまくいくということである。

• つまり私たちのように10に馴染みのない文化圏の人たちならば別に10に基づく記数法を用いる必要はなく、各人たちに適した記数法で良いのである。

• このように基数により数字の表現方法を柔軟にできることも位取り記数法の良い点である。

8. 10に代わるもの

10進法

• 10というのは私たちにとって非常に重要な数字であり、それは両手の指の数の合計値である

• これは人間が手を用いて数を数えていたことに由来しており、そのため人間はその昔、「数」のコードを「10という数」に基づくものとした

• そのため、一般的に私たちの生活でよく用いられる数字は10進法となっている。

10の代わり

• しかし、もし仮に人間社会とはどこか別の場所で、そして「10」という数が我々の社会のようにそこまで浸透していな買った場合、10という数字を見て私たちが思う10を想起できるだろうか？

• つまり何が言いたいのかというと、10といってももしその場所に住む人々の指の数が違っていたら、10という記号が8を表すかもしれないということなのだ

• 私たちの日常にはあまりに10という数が溶け込んでいるため、10と聞いたら「何か特別なもの」と感じる人が多いかもしれないが、位取り記数法の性質を考えれば何も10というのは特別なものでもなんでもないのである

• もう一つ例を出すと、例えばみなさんがイルカになったとして、位取り記数法を用いるとしよう

• この場合おそらくイルカのみなさんは2という数を基にコードをまとめるであろう。

• つまり、人間が手と足の指の合計を元にコードを作ったのと同じように、イルカであるみなさんは2枚の胸びれという特徴を活かしたコードを作りあげるのではないだろうか？

• • この時イルカのみなさんは0と1という2つの数字しか持たない。
  • これは一般的に2進法と呼ばれる記数法である

2進法

• 0と1で構成される2進法は最も簡単な記数法である。当然これ以上は簡単にすることはできない

• そしてこの2進法は単に数を表すだけでなく、実は算術と電気の間の橋渡しをも可能にしている。

• つまり、導線は電流が流れていれば1、流れていなければ0。スイッチはオンつまり閉じていれば1、オフつまり開いていれば0。電球は点灯していれば1、点灯していなければ0。電信リレーは閉じていれば1、休んでいれば0...というように表すと決めると、スイッチと導線と電球とリレーのどれもがこの2進数字0と1で表現できるのである

• このようにコンピュータにとって2進数は切っても切れない関係である

• このためアメリカの数学者ジョン・ワイルダー・テューキーは今後コンピュータが普及するにつれてbinary digit（2進数）という言葉は重要になってくるであろうということを予測し、binary digitを短縮してbitと呼ぶことにしたのである

9. ちょびっとずつビットで

ビット（bit）

• 先ほど登場した2進法は他の記数法と違い特別である。

• • というのもこれ以上単純にすることができないからだ。
  • 2進法より単純にしようとすると、1を捨てることになり、0しか残らなくなる。これでは何も表現することが不可能である

• つまり、2進法は最も単純な記数法であり、そのためビット(bit)という造語も「2進数」という本来の意味を超えて「最小単位」という意味を持つようになった。

• 具体的には今日我々がビットを使用する際に思い起こされる意味の**「情報の最小単位/基本構成単位」**という意味が付加されたのである。こうして今やビットは2進数字という意味を超えて扱われるようになった。

• • これはどういうことか？というと、モールスコード・文字（書き言葉）・点字・10進数...など情報を伝えるためのコードはたくさんあるが、その中でも1ビットがもっとも単純な情報を表すコードなのである。
  • ビットより小さいものはそれはもはや情報ではない。

• そして当然このビットも複数用いることでより複雑な情報を伝えることが可能になる。

数字による情報表現

• さてここから情報伝達の手段としてビットを用いた表現法を見ていくのだが、その前にこうした「数字による情報表現」に馴染みのない人ももしかしたらいるかもしれないので、そちらに少し慣れておこう

• • 例えば日常生活において数字が数以外の別の情報を表している例として有名なのが、電話番号。
  • 電話番号は当然だが、数ではない。それはいわゆる「識別番号」としての役割を持つ数字となっている。
  • つまり、「ものを区別するためだけに使用される数字」なのである。

• 他にもこのような識別番号としての数字としては、郵便番号や車のナンバーが存在する

• これは人間世界だけでなく、コンピュータの世界でも同じことが言える。

• 例えばコンピュータの世界では、何か文字や色を扱う際にはそれらを区別するための識別番号が用いられる

• 有名なASCIIコードは、この文字と数字との対応関係を表したコード体系である。

情報伝達にビットを使用する例①

• ここから先は情報伝達にビットを使用する例をいくつか見ていく

• 1つめはポール・リヴィアが英軍の来襲をアメリカ植民地に知らせた方法。

• ポール・リヴィアではランタンが2つ常に吊されており、英軍が次の３つの可能性について**ランタンが点灯しているかどうか？**で判断した

  • ①陸路で侵入
  • ②海路で侵入
  • ③侵入していない

• 例えば2つのランタンどちらも点灯していない場合は「英軍がまだ侵入していない」ことを表し、もしランタンのどちらか一方が点灯していれば「英軍が陸路から侵入」、どちらも点灯されれば「英軍は海路から侵入」ということを示しているとする

• ここで各ランタンはビットであり、点灯されたランタンは1、点灯されていないランタンは0と見ることができる

• つまりランタンは情報の最小単位である

• そして、今回の場合来襲の有無だけでなく**「どこから」**侵入してくるのか？も知りたいため計3つの可能性を表すコードが必要となる

• これには当然1つのランタン（ビット）では対応できず、もう1つランタンが必要となる。つまり2ビットで情報を伝達する必要がある。

• まとめると以下のようなコードを用いて情報を伝達する

• 00 = 英軍は今夜は来ていない

• 01 = 英軍は陸路で来ている

• 10 = 英軍は陸路で来ている

• 11 = 英軍は海路で来ている

• ここで2ビットあれば4つの情報を伝達できるように感じるがここでは3つの情報だけに留めてあるのに気づく。これは専門用語で言えば冗長性を用いたことになる。

• つまり、ノイズの影響を受けないようにするためコードを冗長化したということである

• さてここまでの話で大切なことは、**「情報とは2つかそれ以上の可能性のうちからの選択である」**ということである。

• 例えば私たちが誰かに話しかけるときに用いる単語や言葉というのは、全てお互いの辞書という「可能性」の中から選択して出てきているものであり、もし仮に各人の辞書の全ての単語に1から番号をつけたとすると、単語ではなく番号でのやりとりも可能になるのである。

• そしてここまで見てきたように、もし複数の可能性からの選択として捉えられる情報であるなら、全てビットを用いて表現できるということが言えそうではないだろうか？

情報伝達にビットを使用する例②

• 次に映画評論家のロバート・エバートとジーン・シスケルが映画に評価を下す際の方法

• 彼らは映画の最終的な評価を下す際に際に親指の上げ下げで評価を行った。実際彼らが映画の際にどういう評価を下したのか？は彼らの親指にさえ注目していればいいのである

• つまり、親指の上げ下げというのが1ビットの情報となり、彼らの2本の親指の上げ下げで2ビットの情報を伝えているのである。

• 具体的には第1のビットをシスケルのビット、第2のビットをエバートのビットとすれば次の4つの可能性を1組のビットで表現することができるのである

  • 00 = 2人とも気に入らなかった
  • 01 = シスケルは気に入らなかったが、エバートは気に入った
  • 10 = シスケルは気に入ったが、エバートは気に入らなかった
  • 11 = 2人とも気に入った

• ここからもし友人に「シスケルとエバートの評価はどうだった？」と聞かれれば、「シスケルは親指を上げて、エバートは親指を下げた」とか「シスケルは気に入って、エバートは気に入らなかった」と答える代わりに**「イチゼロ」とさえ答えておけば良いのである。**

• これに加えて、友人が「どっちがシスケルのビットでどっちがエバートのビットか」を知っていて、かつ「1が良い/0が悪い（1が親指の上げ/０が親指の下げ）」を意味することを知っていれば間違いなく意味が通じるだろう。

• つまり大切なのは、あなたの友人は事前にこのコードの対応関係を知っていなければならないということである

• さらにこの対応関係はどちらでも良い。例えば「1が悪い/0が良い（1が親指の下げ/０が親指の上げ）」としても良くて、これは単なる恣意的な割り当てなのである。

• つまりもう一度いうが、必要不可欠なのはそのコードを使う全員が0と1のビットの意味を知っていることである。

• また個別のビットまたはビットの集まりが何を意味するのか？は当然ながら常に文脈や状況に応じて変化していく

• 先ほどのシスケル・エバートにしても彼らがどの映画について言及しているのか？を知っておかないと意味がなくなるし、さらに①のランタンにしてもランタンではなく懐中電灯を用いてしまったら全く意味が通じなくなってしまう。

情報伝達にビットを使用する例③

• 次に「Entertainment Weekly」誌の評価の与え方について見てみよう。

• こちらの雑誌では映画だけでなく、テレビ番組、CD、本、CD-ROM、Webサイト...と様々なものに評価を与えており、その評価の範囲はA+~Fまでである

• この評価の数を数えてみると13段階の評価があることがわかる。さてではこの13段階の評価を表すためには一体どのくらいのビットが必要だろうか？

• 答えは4ビット必要で、正確には以下のような割り当てとなる。

  • 0000 = F
  • 0001 = D-
  • 0010 = D
  • 0011 = D+
  • 0100 = C-
  • 0101 = C
  • 0110 = C+
  • 0111 = B-
  • 1000 = B
  • 1001 = B+
  • 1010 = A-
  • 1011 = A
  • 1100 = A+

• 当然ここからもわかる通りビットは多ければ多いほど表現できる情報（可能性）が増える

• そしてこの複数ビットでどれほどの数の情報を表現できるのか？ということを考える際に役立つのが数学の組み合わせ論であることは以前の章でも述べた。

• つまり、可能なコードの個数は2の「ビットの個数」乗に等しくなる。

ビットの個数	コードの個数
1	2^1 = 2
2	2^2 = 4
3	2^3 = 8
4	2^4 = 16
5	2^5 = 32
6	2^6 = 64
7	2^7 = 128
8	2^8 = 256
9	2^9 = 512
10	2^10 = 1024

情報伝達にビットを使用する例（その他）

• ここまで情報伝達にビットを使用する例を見てきたが、当然今まででてきたコードも全てビットで表現することが可能である。

• 例えばモールスコード。

• これはドット（短い点滅）とダッシュ（長い点滅）を用いて各文字を表す方法であり、以前の章で以下のような特徴を持つものと仮定してやりとりをするとスムーズにコミュニケーションを図れると述べた

  • ダッシュの長さはドットの長さの3倍
  • ドットとダッシュの間のポーズはドット1つ分
  • 文字同士の間のポーズはダッシュ1つ分
  • 単語同士の間のポーズはダッシュ2つ分

• これを少し単純化して、ダッシュの長さはドットの長さの２倍であると仮定しよう。

• こうすることで、ドットは1が1個、ダッシュは1が2個、空白は0がいくつかと対応づけることができ、アルファベットは以下のようにビットで表すことができるようになる

アルファベット	数字	アルファベット	数字	アルファベット	数字
A	101100	J	101101101100	S	1010100
B	1101010100	K	110101100	T	1100
C	11010110100	L	1011010100	U	10101100
D	11010100	M	1101100	V	1010101100
E	100	N	110100	W	101101100
F	1010110100	O	1101101100	X	11010101100
G	110110100	P	10110110100	Y	110101101100
H	101010100	Q	110110101100	Z	11011010100
I	10100	R	10110100

• このようにビットを用いることでありとあらゆる情報を表現することができるようになり、ビットは**「情報の最小単位」**としての役割を担うことがよくわかる

• しかし、本質的にはビットもただの"数"であることを忘れてはいけない。

• つまり、ビットが他の情報を表現する際には、

  • 可能性の数を数える
  • 対応関係を明確にする

　ということを決して忘れてはいけないのである。

10. 論理とスイッチ

ビットと論理

• ここまで見てきたビットだが、実は論理学でも重要な役割を持つことになる。

• つまり**「ある命題が真である = 1」「ある命題が偽である = 0」と対応付けを行うことで、より論理学を明確にすることができるようになるのである**

論理学

• そもそも論理学とは古代ギリシャで発展したもので、**「真理とは何か？」**を追求するための手段であり、哲学の一形態と見なされていた。

• もう少しわかりやすくいうと、論理学とは**「すでに知っていることからまだ知らないことをどのようにして正しく導けば良いのか？」**を考えた学問であった。

• 例えば、アリストテレスの論理の基礎は3段論法と呼ばれるもので、最も有名な3段論法として次のようなものがあった

  • 全ての人間は死すべきものである。
  • ソクラテスは人間である。
  • ゆえにソクラテスは死すべきものである。

• このように論理学とは正しい推論を追求するための学問であり、**「この正しい推論にはいくつかのパターンが存在する」**ということを見つけたのがアリストテレスであった。

• 上の例で出てきた「3段論法」もそのようなパターンの一種であり、3段論法では**「ある二つの前提が正しいと仮定した場合に、必ず正しい結論を導くためのパターン」**をまとめた

• 上の例の推論は定言的3段論法と呼ばれるものであり、①全てのPはQo ②xはPo という2つの前提から「xはQo」という結論を導くためのパターンである。

• また他の例としては、次のようなものがある

  • 私はスープを選ぶか、またはサラダを選ぶ。
  • 私はスープを選ばない。
  • 従って、私はサラダを選ぶ。

• こちらは選言的3段論法と呼ばれるもので、①Pか、もしくはQo ②Pではない という2つの前提から「Qo」を導くためのパターンである。

• こうしてアリストテレスにより、正しい推論を導くためのパターンがどんどん追求されるようになっていった

• そして中世以降、こういったパターンをたくさん学ぶことが**「論理学」**とされてきた

論理学と数学

• そうしたパターンの追求がされる一方、このような論理学と数学を結びつけることができないだろうか？と悪戦苦闘する数学者もいた

• その代表例が19世紀半ばに現れたジョージ・プールという人物で、彼は論理学を数学の記号などを用いて表すことに成功した

• プールにより通常は文章で表されていた論理学が記号として捉えられるようになり、推論のパターンが可視化されやすくなった

プール代数①：概要

• プールは通常の代数とよく似た代数を発明し、この代数は一般的にプール代数と呼ばれる

• 代数と言っても伝わりづらいと思うので、ざっくり正しい推論を表すための**「計算の仕組み」**と捉えればOK

• 通常の代数では演算対象は「数（数字で表される）」を表し、演算子は「それらの数の組み合わせ方（+や×）」を示していた。

• しかし、プール代数では演算対象は数ではなく、クラスを表している。クラスとは単にもの集まりであり、後に集合と呼ばれるものである。

• つまり、プールは今まで縛られていた数というパラダイムから離れ、その数をさらに抽象化したものを対象に考えようとしたのである。ここがプールの天才的な一面である。

プール代数②：論理演算子

• そして当然プール代数では従来と同じような演算子も使う。しかしながら、その演算子は従来の演算子をより抽象的に捉えているため、意味合いが大きく異なっている。

• このような演算子を**「論理演算子」**と呼ぶ。

• 例えば従来+と×は足し算と掛け算を示すために用いられるが、プール代数では+はクラスの結びを、×はクラスの交わりを意味している。

• これだけでは意味がわからないと思うので、少し例を出して考えてみよう

  • いま猫の集合を考える
  • 猫は当然であるが、オスまたはメスであり、ここで便宜的にオス猫の集合をM、メス猫の集合をFとしよう。（ただしこれらはあくまで特定の性質を持った猫の集合を表していることに注意しよう。猫の数を表しているわけではない）
  • 他にも褐色の猫の集合をT、黒色の猫の集合をB、白色の猫の集合をW、他の色の猫の集合（T、B、Wに属さない全ての猫）のクラスをOとする
  • また去勢されている猫の集合をN、去勢されていない猫のクラスをUとしよう
  • この時B+Wというのは、Bという集合とWという集合の結びを表しており、具体的には白か黒である全ての猫の集合を指す。
  • さらにF×Tといえば、Fという集合とTという集合の交わりを表しており、メスであり褐色である全ての猫の集合を指す。（これはいわば形容詞「メスの」と「褐色の」をつなげたものと考えたらわかりやすいだろう）

プール代数③：交換律/結合律/分配律

• • また従来の代数では私たちは無意識的に交換律/結合律/分配律といった規則を用いているが、プール代数でもこれは成り立つ

  • ちなみに交換律というのは、演算子の両側の記号を入れ替えても良いことを意味していて、具体的にはA + B = B + A や A × B = B × Aのような規則のことである

  • さらに結合律というのは、A + (B + C) = (A + B) + C や A × (B × C) = (A × B) × C のような規則のこと

  • 最後に掛け算は足し算に対して分配律を満たすと言われており、具体的には以下のような規則が成り立つ

  • A × (B + C) = (A × B) + (A × C)

• 例外は分配律であり、こちらはプール代数の場合+演算子は×演算子に対する分配律を満たしている。具体的には以下のような規則がプール代数では成り立ち、これは従来の代数では偽である

• W + (B × F) = (W + B) × (W + F)

• これは「白い猫と黒いメス猫の結び」は、「白猫と黒猫の結び」と「白猫と雌猫の結び」の交わりと同じであるというもので、実際にベン図を書いてみると成り立つことがわかるだろう

プール代数④：1と0

• さらに、プール代数を理解するには、もう2つの記号が必要となる。それは1と0である

• 1は「全体」を表し、議論の対象全てを指す。

• 今回の例で言うと1は「全ての猫の集合」となる

• そのため当然M + F = 1のような式も成り立つ。これはメス猫とオス猫の結びが全ての猫の集合であることを意味し、当たり前である

• また同様に考えればT + B + W + O = 1が成り立つこともわかるだろう

• そして1という記号の特別な特徴はマイナスという記号を用いることが可能になるということ

  • つまり、例えばN + U = 1について式変形すると1 - U = Nという式が成り立つということである
  • これは全体から去勢されていない猫の集合を取り除いたら去勢されている猫の集合と同じという意味であり、当然のことである

• さらに0は**「空きクラス」**を指す。これは何もないクラスのことであり、例えば二つの互いに素の集合の交わりをとったときに生じる

• 例としてはM × F = 0などがある

• また最後に一つ注意点としてプール代数は従来の代数の抽象的な概念であるといっても、一部は従来の代数と同様に機能することがあるということを挙げておきたい

• これは主に0と1を用いる場合に生じる

• 例えば全ての猫とメス猫の交わりは当然メス猫であり、これはプール代数で表すと以下のようになる

• 1 × F = F

• また同様に空集合とメス猫の交わりは空集合であり、0 × F = ０となる

• しかし同じように見える結果がある一方当然違ってみえる結果も存在する

• 例えば全ての猫とメス猫の結びは全ての猫の集合である。これは式で表すと1 + F = 1である。これは従来の代数ではあまり意味をなさない

プール代数を用いた3段論法の証明

• プール代数を用いることで少し前に例に出したアリストテレスの3段論法を数学的な方法で解くことが可能になる

• • 全ての人間は死すべきものである。
  • ソクラテスは人間である。
  • ゆえにソクラテスは死すべきものである。

• この例においてすべての人間の集合をP、死すべき定めにあるものの集合をM、ソクラテスの集合をSで表すとしよう

• 最初の「全ての人間は死すべきものである」という命題は、「人間の集合と死すべき定めにあるものの集合の交わりが人間の集合」と言い換えることができる。数式では、P × M = P

• さらに「ソクラテスは人間である」は同様に考えると、S × P = Sと表せる

• さてここから通常の代数のように計算していこう。まず第一式を第二式に代入すると、S × (P × M) = Sとなる

• これに結合律を用いると、（S × P） × M = Sとなる。

• さらにS × P = Sであることがわかっているので、これはS × M = Sと言える。

• これはどういうことか？というと、「ソクラテスと死すべき定めにあるものの交わりはソクラテスである」ということを言っている。つまり、3つ目の命題が真であることが証明されたのである。

「または（OR）」と「かつ（AND）」と「ではない（NOT）」

• プール代数はこうした推論パターンを数式にして見えやすくすることを可能にしたが、それ以外にも実は使い道がある

• それは**「何かが一定の条件を満たすかどうかを判断する」ことにも使えるのである**

• この「条件が満たすかどうか」の判断には「結び」や「交わり」といった概念は少しわかりづらいので、「または（OR）」と「かつ（AND）」という馴染み深い表現にこれらを置き換えよう

• さらに、1という全体集合を導入したときに登場したマイナスという概念も**「ではない（NOT）」**という表現に置き換える

• まとめると以下のようになる

  • 結び（+）= OR
  • 交わり（×）= AND
  • 全体から除く（1-） = NOT

真偽テスト①：真偽値の導入

• さてではプール代数のもう一つの使い方である「あるものが条件を満たすかどうかの判断」（以下真偽テストと命名）について見ていこう

• 例として以下のような真偽テストを考えてみる

  • 「オスで去勢してあって白か褐色の猫」か「メスで去勢してあって白以外の色の猫」か「黒色の猫」
  • プール代数で表すと以下のようになる
  • （M × N × (W + T)） + (F × N × (1 - W)) + B
  • ここでペットショップの店員が「去勢されていない褐色のオス猫」を連れてきた場合の真偽テストの結果を考えてみる

• この真偽テストを考えるには、このプール代数を別の形式に置き換えるとわかりやすくなる

• ここでは**「今まで集合として扱っていた文字の代わりに数を割り当てる」**ということを行ってみる

• 具体的には、**0と1を集合に割り当てる。1は「真」でこの猫は条件を満たし、0は「偽」**でこの猫は条件を満たさないとする。

• すると先ほどの真偽テストの真偽を表す式は以下のようになる

• (1 × 0 × (0 + 1)) + (0 × 0 × (1 - 0)) + 0

• 当然1を割り当てられるのは、「M」と「T」だけである。（この猫はオスで褐色だから）

真偽テスト②：ORとANDの計算表

• 次にしなければならないことは上の真偽を表す式を簡単にすること。

• まずORとANDの真偽値の計算表は以下のようになる

OR	0	1
0	0	1
1	1	1

AND	0	1
0	0	0
1	0	1

• これをみるとAND、つまり×は普通の掛け算と全く同じ結果になる。

• しかしOR、つまり+の場合には一部例外が発生する

• それは1 + 1 = 1となることである。これは違和感かもしれないが、よく考えれば当たり前のことである。

• 例えば「ある猫が白猫か黒猫である」という命題に対し、「その猫は白猫」と「その猫は黒猫」のそれぞれの条件を両方満たしているとする。すると、この命題は当然「真」になる

真偽テスト③：計算

• さて、ではこれらの計算表を用いて実際に真偽テストを行なっていこう

• まず今回計算する真理式を再喝すると以下のようであった

• (1 × 0 × (0 + 1)) + (0 × 0 × (1 - 0)) + 0

• これを式変形しながら解いていくと以下のようになる

• (1 × 0 × (0 + 1)) + (0 × 0 × (1 - 0)) + 0　= (1 × 0 × 1) + (0 × 0 × 1) + 0 = 0 + 0 + 0 = 0

• つまり、この式は「偽」であることがわかる

• これは要は「去勢されていない褐色のオス猫」は条件「 『去勢してあって白か褐色の猫』か『メスで去勢してあって白以外の色の猫』か『黒色の猫』」を満たさないということになる

• このようにプール代数を少し変形して用いることで、真偽テストのようなものを行うことができるのである。

プール代数と電気回路の一体化①

• 実は先ほど見てきた真偽テストは、以下のようなスイッチと電球を用いた電気回路により判定することができる

• この発想の飛躍はコンピュータの歴史の中で非常に重要なものであり、これこそが2進数で動くコンピュータの設計と構築を可能にするものとなった。詳しくは後で述べていく。

• ではまずこの実験の手始めとして電球と電池を次のようにつないでみる

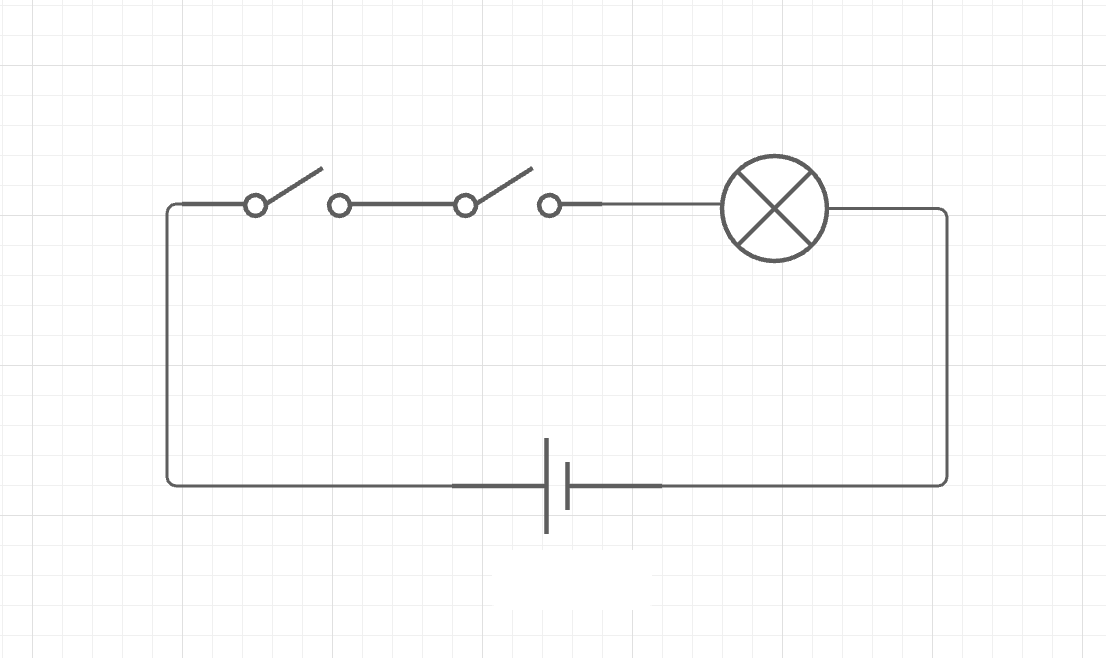
• このように前後にスイッチを連続して繋ぐ方法は直列と呼ばれている。左（右）側のスイッチだけを閉じたとしても何も起こらない。

• この回路の電球が点灯するのは、 左のスイッチ「と」右のスイッチの両方のスイッチを閉じたときだけである

• ここで大切なのは、「『と』=『and』」である。つまり、左のスイッチ「かつ」右のスイッチが閉じられるときに電球が点灯し、回路に電流が流れるということである

• この性質からこの回路は先ほどの真偽テストと同じように考えることができるのではないだろうか？

• つまり、電球は「両方のスイッチが閉じているか？」という問いに対しての答えとなっていて、この回路の動きは次の表のようになるのである

左のスイッチ	右のスイッチ	電球
開	開	点灯しない
開	閉	点灯しない
閉	開	点灯しない
閉	閉	点灯する

• • さてここで思い返して欲しいのが、第9章で2進数字つまりビットにより数から映画評論家エバートの親指の向きに至るまであらゆる情報を表現できるということ。
  • 例えば0は「エバートの親指は下向き（悪い）」を、1は「エバートの親指は上向き（良い）」を意味していた

• これと同様に考えれば0は「スイッチは開いている」を意味し、1は「スイッチは閉じている」を意味すると言うことができる

• またスイッチだけでなく、電球も二値情報をとるためビットで表せて0は「電球は点灯していない」を、1は「電球は点灯している」を意味すると言えるのである

• ここから先の表を書き直すと以下のようになる。さらに左スイッチと右スイッチの区別をなくしても結果が変わらないことを考慮したらさらに以下のような表へと書き換えることができる

左のスイッチ	右のスイッチ	電球
0	0	0
0	1	0
1	0	0
1	1	1

直列スイッチ	0	1
0	0	0
1	0	1

• さてこの表はどこかで見覚えないだろうか？そう、先に示したANDの真偽値の表である。

AND	0	1
0	0	0
1	0	1

• つまり何が言いたいのか？というとこの単純な回路はプール代数のAND演算を実行しているということである

プール代数と電気回路の一体化②

• では次にスイッチのつなぎ方を変えて以下のような回路を考えてみよう

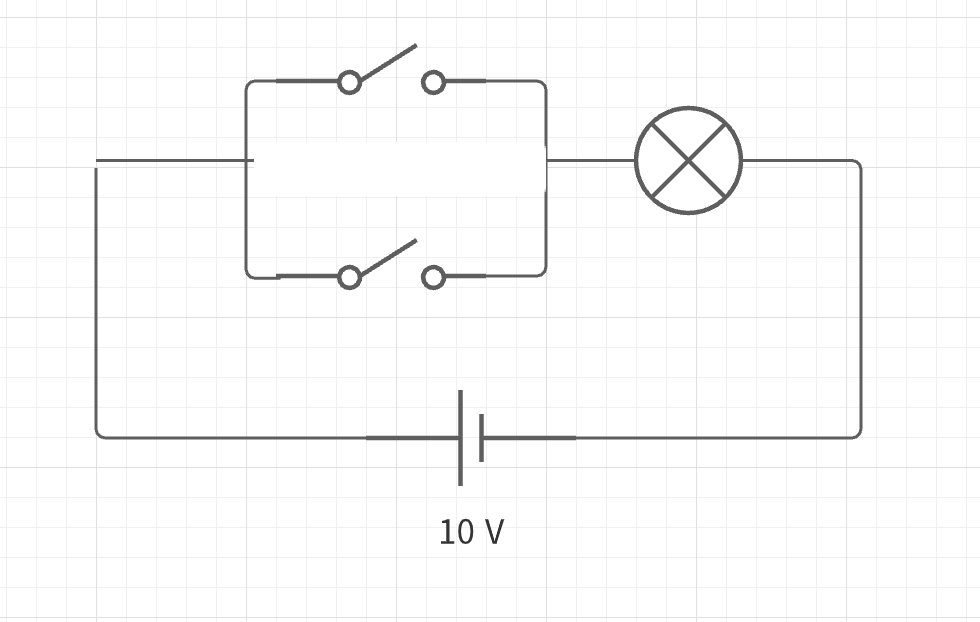
• これらのスイッチのつなぎ方は並列と呼ばれている

• 直列と同様に考えるとこの回路の電球は、「どちらかのスイッチが閉じているか？」という問いに対しての答えになっている

• そしてこの回路の動きをまとめてみると以下のようになる。さらにスイッチ/電球をビットで表したものも加味して考えると以下のようになる

左のスイッチ	右のスイッチ	電球
開	開	点灯しない
開	閉	点灯する
閉	開	点灯する
閉	閉	点灯する

左のスイッチ	右のスイッチ	電球
0	0	0
0	1	1
1	0	1
1	1	1

並列スイッチ	0	1
0	0	1
1	1	1

• この表はOR演算の表と同じである

OR	0	1
0	0	1
1	1	1

• つまり、並列につながれた2つのスイッチはプールのOR演算と同様に機能している。

プール代数と電気回路の一体化③

• さてでは最後に最初に行った真偽テストを電気回路で置き換えて考えてみよう

• 念のため真偽テストを行う対象を再喝しておく

  • 「オスで去勢してあって白か褐色の猫」か「メスで去勢してあって白以外の色の猫」か「黒色の猫」
  • プール代数で表すと以下のようになる
  • （M × N × (W + T)） + (F × N × (1 - W)) + B
  • これに対してペットショップの店員が「去勢されていない褐色のオス猫」を連れてきた場合について考えてみる

• 先ほどの直列⇔論理AND（×）、並列⇔論理OR（+）という対応関係を頭に入れてこのプール代数で表された式を電気回路で置き換えると以下のようになる

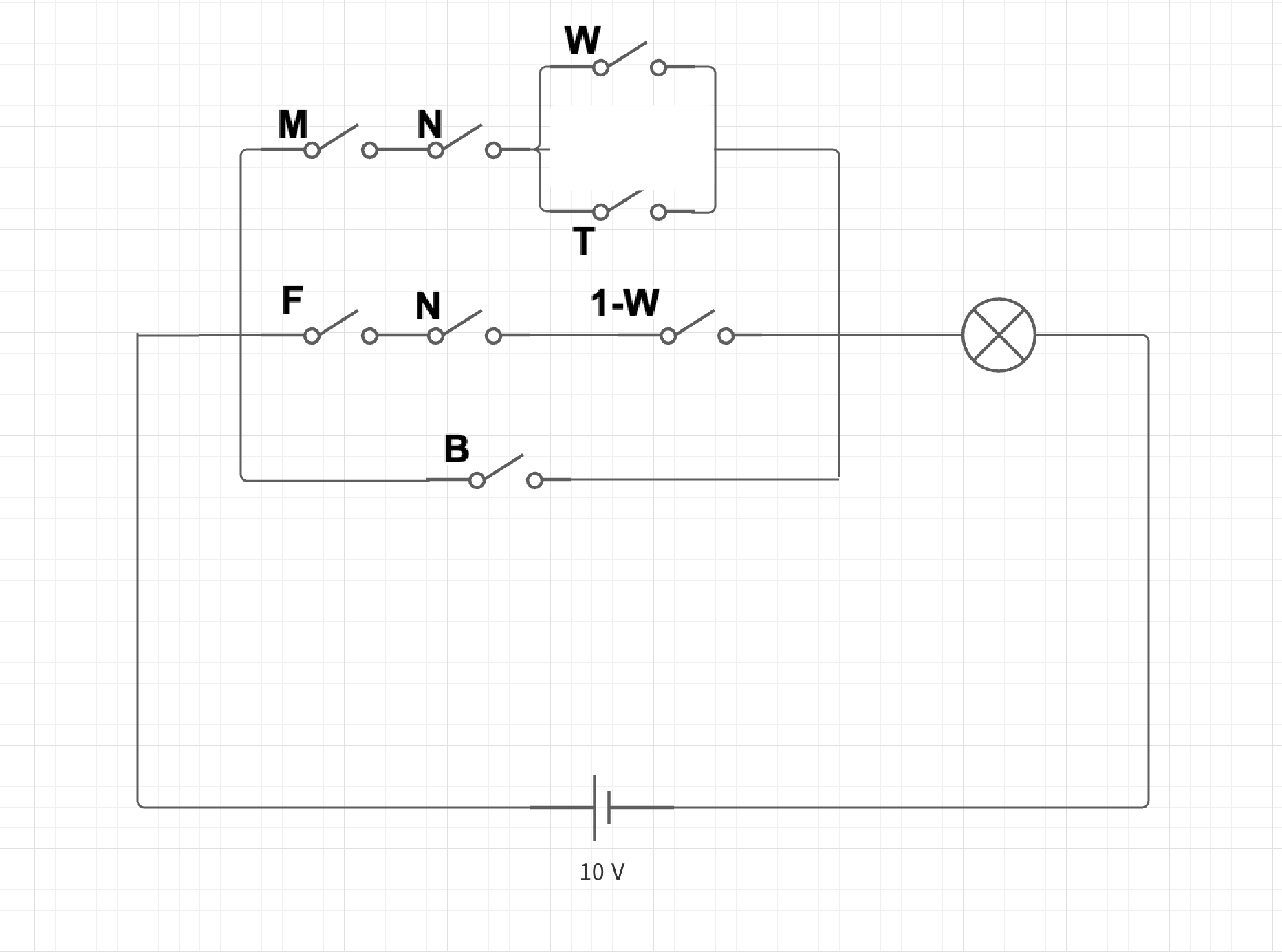
• 回路の各スイッチはプール式と同じ文字を用いている。

• ここで「去勢されていない褐色のオス猫」に相当するスイッチを閉じると以下のようになる

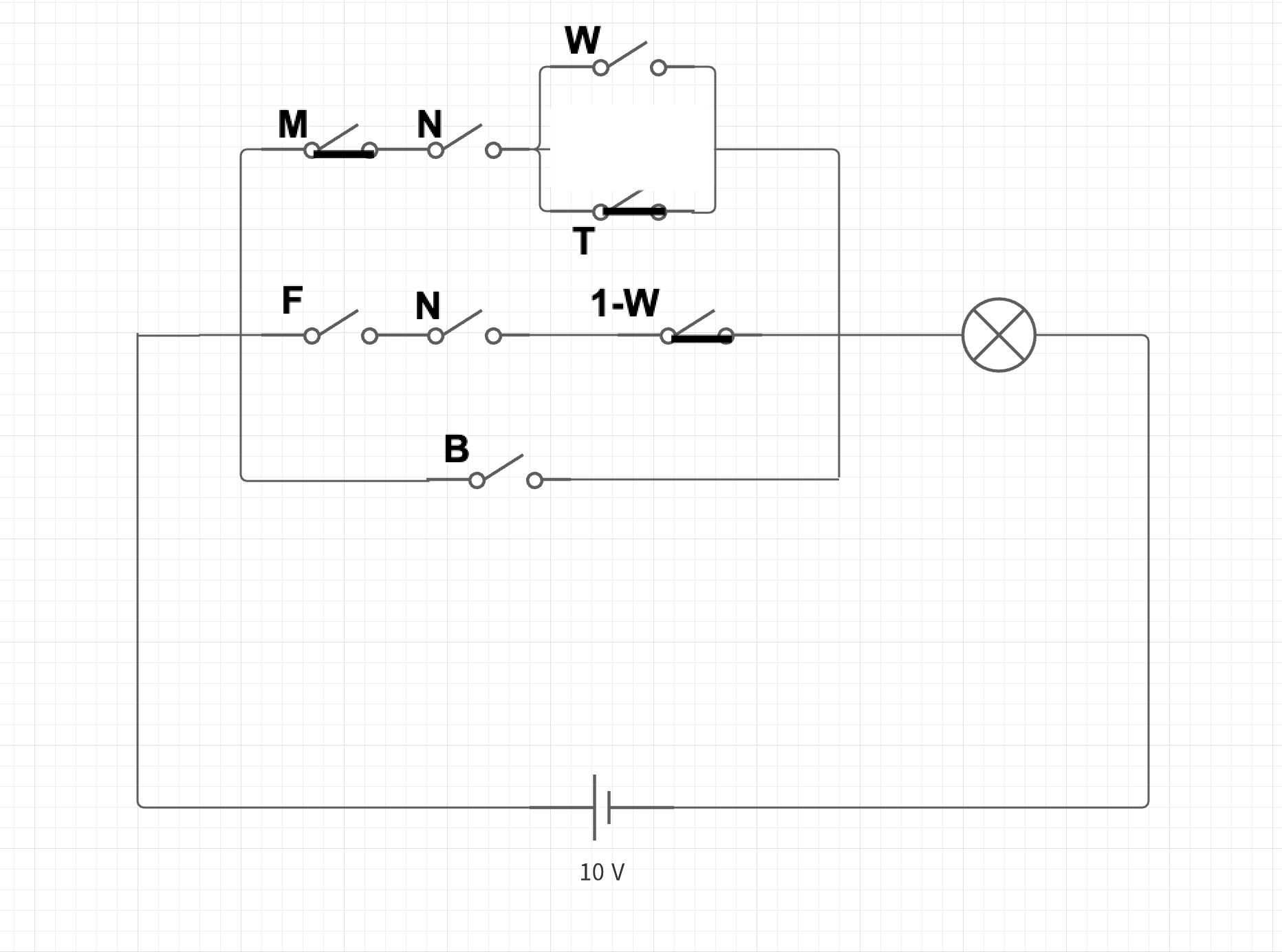
• この回路を見た場合、電流が流れないことは明らかなので、電球は点灯しない。つまり結果は偽（0）である
• 次に店員が「去勢された灰色のメス猫」を連れてきた場合はどうだろう？

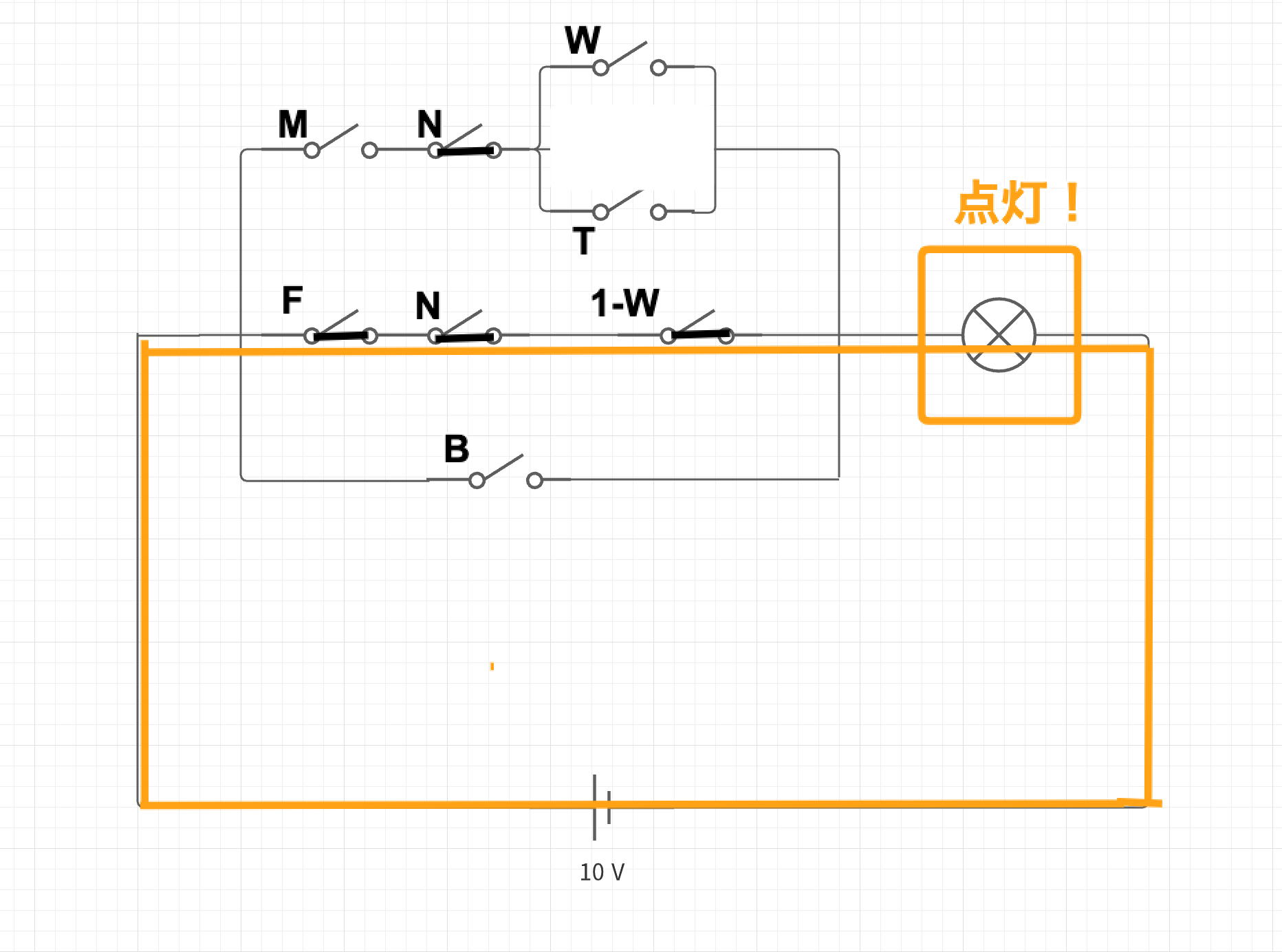
• この場合回路が完成するため、電流が流れ電球が点灯する。つまり、真偽テストの結果は真（1）である。

まとめ

• かなり長くなってしまったが、まとめると

  • 論理学を数式としてとらえるために**「プール代数」**という計算の仕組みが作られた
  • このプール代数による計算は、スイッチと電球を用いた電気回路を用いて表現可能
  • プール代数と電気回路を結びつけるのは他ならないビットである。つまりプール代数の真偽、電気回路のスイッチのオンオフ、電球の点灯/非点灯にそれぞれ1と0を割り当てることによりプール代数と電気回路は一体化する
  • これにより2進数で動くコンピュータが理論上設計可能になった

• ところで実際ジョージ・プールはこのような回路を配線したのだろうか？

• 答えはノーである。

• これは白熱電球がプールの死後15年経ってからようやく発明されたことが関係している。つまり、先ほどの電気回路のように電球を用いることができなかったのである

• しかし、彼が生きていた時代にはすでにサミュエルモースにより電信はすでに実証済みであり、先ほどの電球の代わりに「電信のリレー」を用いればプール代数と電気回路を統合して考えることは可能だったのである

• だが、この時代にプール代数のANDとORと、単純なスイッチの直列と並列の配線を結びつけたものは誰1人としていなかった。

• そしてここからしばらく経ったのちにようやく**「電信のリレー」**が用いられることで、プール代数と電気回路は一体化していくのである。

11. ゲート

スイッチ回路の簡易化

• 先ほどの章でも述べた通りプール代数とリレーの結びつきを明らかにしたのは、リレーが発明されてしばらく経ったのち

• 具体的には19世紀にクロード・エルウッド・シャノンが1938年に書いた論文によってこれらの同等性が発見された

• 1938年以前にも、スイッチを直列に繋ぐと両方のスイッチを閉じたときだけ電流が流れ、並列につなぐと一方を閉じただけで電流が流れるということを多くの人が知っていた

• しかし、プール代数の全ての道具を使用して、スイッチ回路を設計できることを明確にまた厳格に示したのはシャノンが初めてであった

• またさらにネットワーク（先ほどのようにプール代数の計算式を表した電気回路）を記述するプール式を簡単にできればそれに応じてネットワーク自体も簡単にできることも示した

• 例えば（M × N × (W + T)) + (F × N × (1 - W)) + Bも分配律を用い、Nを括り出すことで以下のような簡単な式になる

• N × ((M × (W + F) + (F × (1 - W))) + B

• このネットワークは以下のようになり、スイッチを一つ減らせる

• しかし、これでもまだスイッチが実は多い

• 理論上はスイッチがビット情報であることを考慮すると、4つで十分である。なぜなら性別に関するビットが1つ、去勢に関するビットが1つ、色に関するビットが2つでいいからである。（色は4色であるため）

• 色に関しては、例えば両方のスイッチがオフなら白、1つがオンなら黒、別の方がオンなら褐色、両方がオンなら他の色とすれば良い

• これらの情報から猫選びのための以下のようなコントロールパネルを作ることができる。このコントロールパネルの適当なスイッチをオンにするとその結果が電球の点灯/非点灯になって現れる

• 簡単に以下の装置を説明しておくと、スイッチは上向きならオン（閉）、下向きがオフ（開）である。

• またラベルBの左のスイッチは単独でオンなら黒を、ラベルTの右のスイッチは単独でオンなら褐色を表す。そしてこれらの両方のスイッチがオンならその他の色、オフなら黒を表すとする

• 他のスイッチは見た通りである

• コンピュータ用語で言えば**このスイッチは入力デバイス、電球が出力デバイスである。**入力スイッチは猫についての4ビット情報に対応し、これにより電気回路を制御できる

• この例だと「メスの去勢されていない黒猫」に設定されているので、条件をみたし点灯する

論理ゲート

• 上で登場したコントロールパネルを機能させる回路はどのように設計すれば良いだろうか？

• それにはまずシャノンの提唱した「論理ゲート」の存在を知る必要がある

• シャノンの論文の題は「リレーとスイッチ回路の記号的分析」であり、彼のいうリレーは第6章で見た電信のリレーによく似たものであった

• そしてスイッチと同様にこのリレーも直列や並列につないで**単純な「プール代数による計算（論理AND/OR）」**をさせることが可能である。

• このリレーの組み合わせにより論理計算を可能にしたものを「論理ゲート」と呼ぶ。

• ゲートというのは水や人を通す通常のゲートと同様、電流を遮断したり通したりすることを指す。電流をコントロールすることで論理の計算を可能にすることから「論理ゲート」と言われる

• またリレーがスイッチと違うのは、手動ではなく他のリレー（電磁石）によりオン/オフできるという点である。

• つまりリレーの組み合わせにより論理ゲートを作ることができ、そしてその論理ゲートもまた組み合わせ可能であり、それによりさらに複雑な作業（簡単な算術計算など）を実行させることができるのである

• 後の章で論理ゲートをいくつか組み合わせ「2進数加算器」を実装してみる

• ここからもわかるとおり、今まではリレーを「弱い信号を増幅させる目的」で使用していたが、シャノンにより**「電気で制御できるスイッチ」**として使用することに変更されたのである

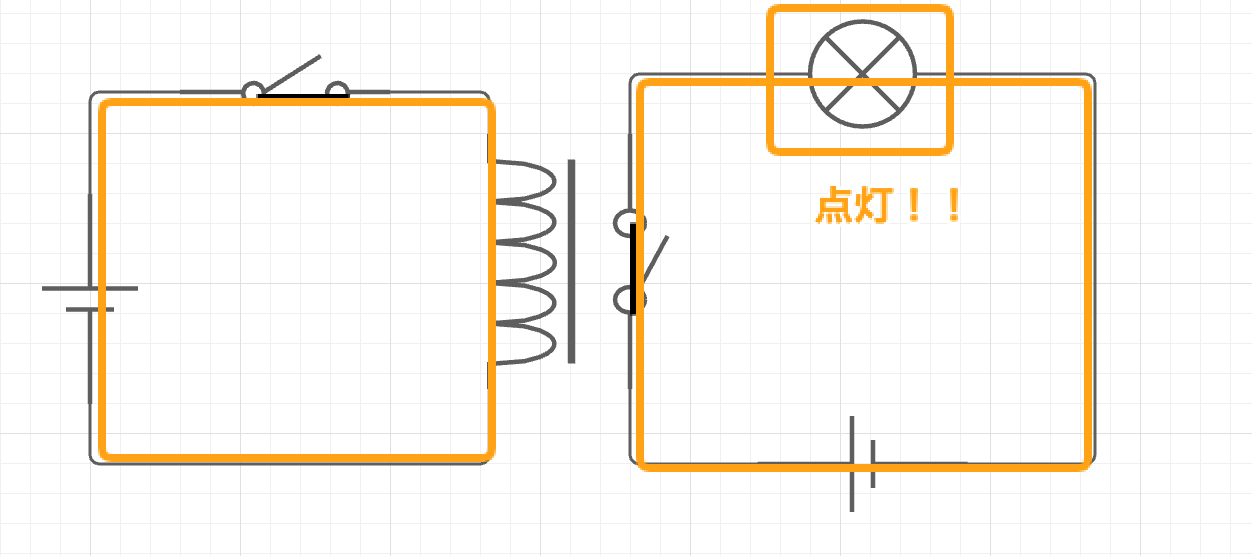
• 例えば以下のようにリレーにスイッチと電球と2つの電池をつないでみよう

• 当然この回路は今左のスイッチが開かれていて電球はオフになっている。このスイッチを閉じると左の電池から電流が流れて鉄棒に磁力が生じ、右のスイッチが閉じられ、電球がオンになる（電信とほぼ同じ）

• この電磁石によりスイッチが閉じられる動作は**「リレーの起動」**と呼ばれている。スイッチがオフにされると鉄棒は磁力を失い、スイッチは元に戻る

• これがリレーの最も基本的な形である。ここからはこのリレーを複数用いて論理ゲートを作っていく。（論理ゲート作成後は、論理ゲートを用いていくためリレーは必要なくなる。）

• また以降では以下のように、先ほどのコントロールパネルに基づいてリレーを**「入出力」**という観点で見ることにする

• つまり電流が入力から流れてくると電磁石が起動し、出力として電圧が発生し、電球が点灯するということである

ANDゲート

• 論理ゲートを構築するにあたって大切なのは**「リレーの組み合わせ」であり、それはつまり「リレーの接続」**である。

• 「リレーの接続」と聞くと一見難しそうに聞こえるが、リレーの入力がスイッチである必要はなく、またリレーの出力が電球である必要がないことを考慮すると簡単にイメージできるだろう

• つまり以下のようにリレーの出力は他のリレーの入力に接続されていてもいいのである

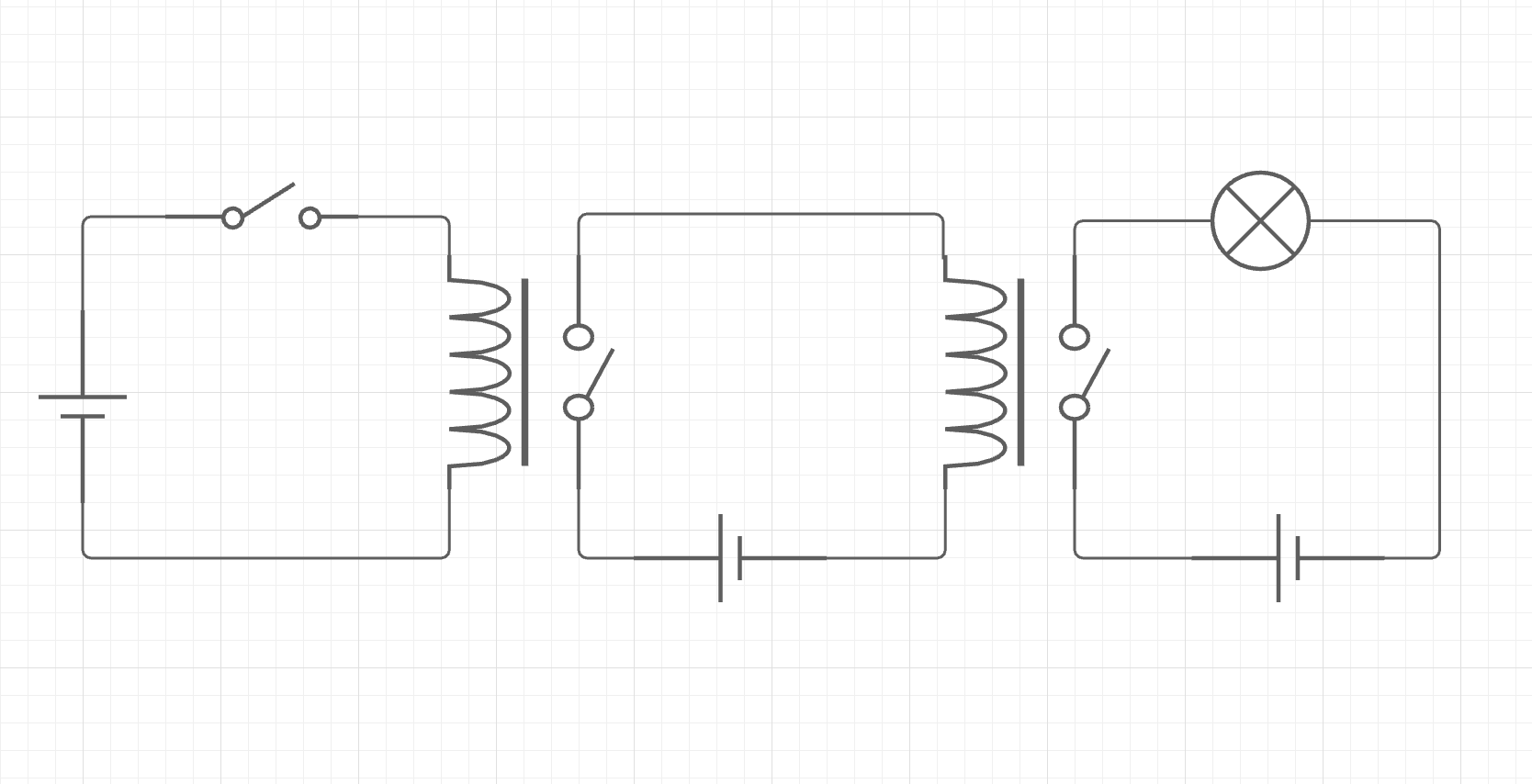
• この回路ではスイッチをオンにすると第1のリレーが起動され、第2のリレーに電圧を提供する。そして次に第2のリレーが起動され、電球が点灯する

• 何度でも言うが、この「リレーの接続」こそが論理ゲート作成のキーである

• これを踏まえた上で、2個のリレーを直列に接続してみよう

• この場合下のリレーの出力は第2のリレーに電圧を供給する。

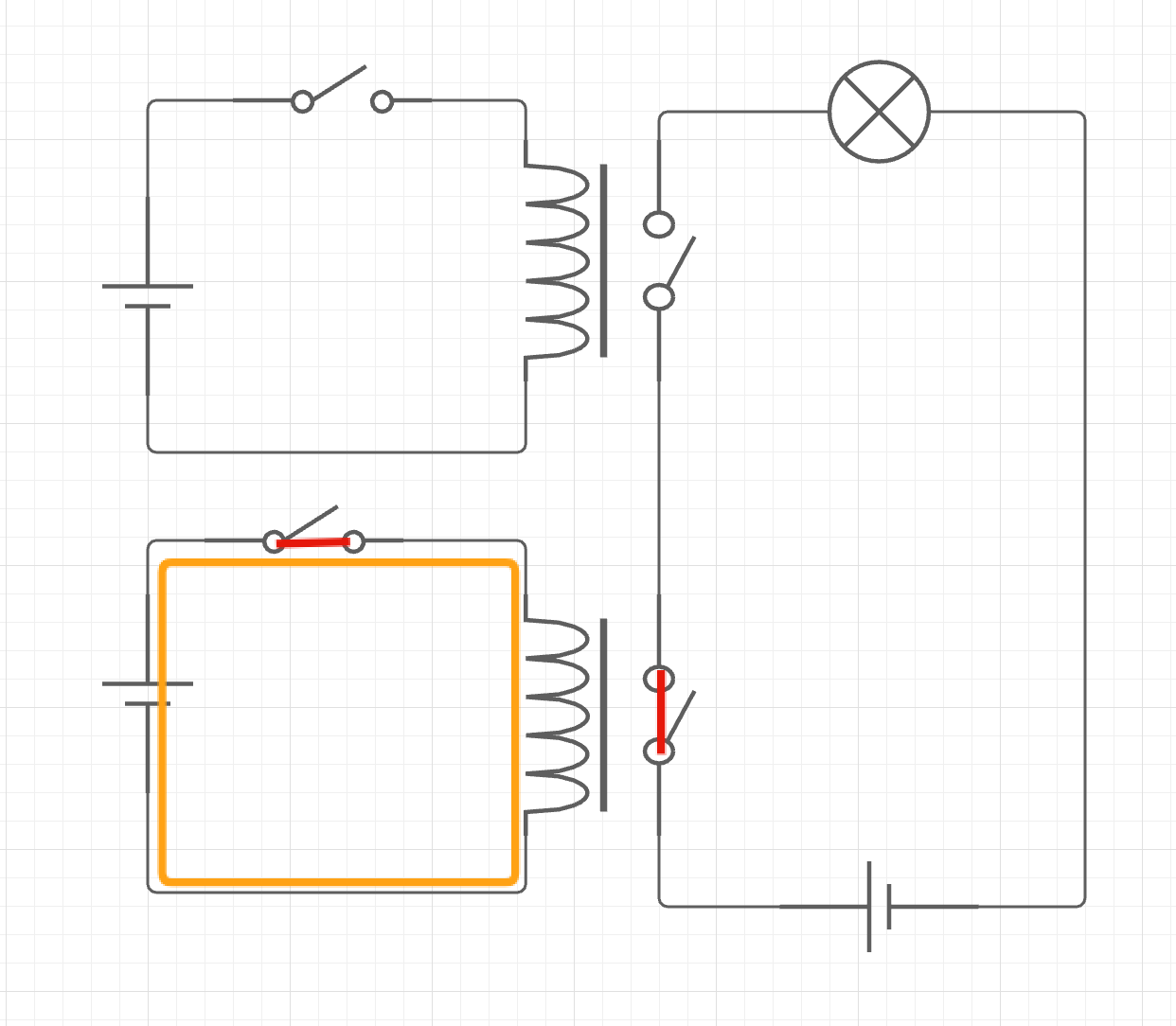
• しかし、下のスイッチだけ閉じても電球はまだ点灯しない。上のスイッチが開いたままでリレーが起動されないからである。

• ここからもわかる通り電球が点灯するのは、両方のスイッチを閉じたときだけである

• つまり、これも前の章で見てきた直列回路と同じで、電球は**「両方のスイッチが閉じているか？」という問いに対しての答え**となっているのである

• この直列につながれた2つのリレーはANDゲートと呼ばれる。

• 図を簡単にするため、ANDゲートは通常以下のような記号を用いられる

• **これは4つある基本論理ゲートのうちのひとつである。**ANDゲートは2つの入力と1つの出力を持っていて、上の図のように左側に入力、右側に出力がくるように描かれることが多い

• そしてこのリレーの直列回路はANDゲートの記号を用いると以下のように表される

• このANDゲートの記号では、直列につながれた2つのリレーの代わりをするだけでなく、下のリレーが電圧につながれていることと、両方のリレーがアースされていることも意味している

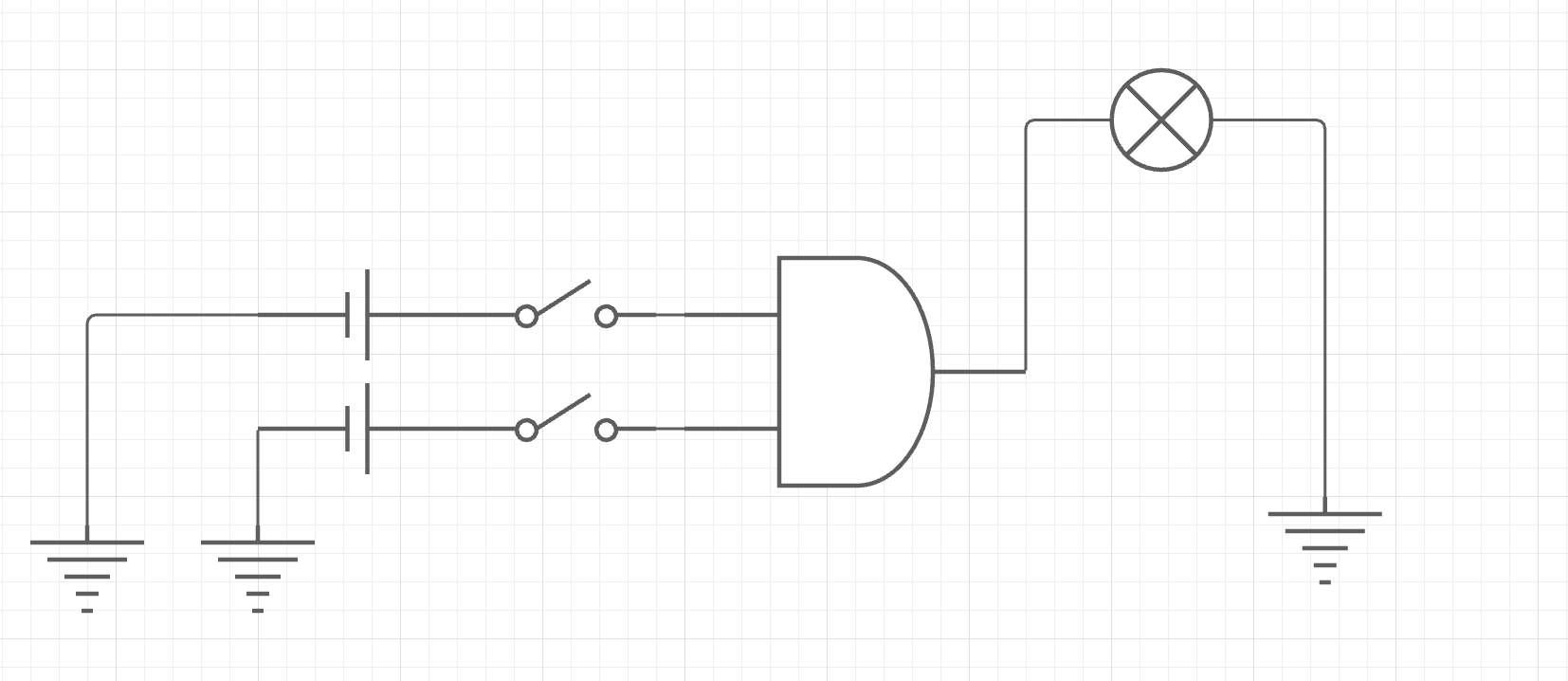
• ANDゲートの入力は必ずしもスイッチに接続される必要はなく、また出力も必ず電球に接続される必要はないのは先ほども言った通りである。

• つまりこれはリレーも論理ゲートも本質的に扱っているのは入出力それぞれでの電圧であることを意味しており、電圧の有無がゲートの入出力の値を決定しているのである

• 例えば以下のようにANDゲートの出力は第2のゲートの入力にもなりうる

• この電球が点灯するのは、3つのスイッチ全てが閉じている時だけであり、上の2つのスイッチが閉じている時だけ、第1のゲートの出力が第2のゲートの第1のリレーを起動する。

• さらに1番下のスイッチは第2のゲートの第2のリレーを起動する。これにより第2のゲートの出力に電圧が生じ、結果的に電球が点灯する

• さてここで電圧がない時を0とみなし、電圧があるときを1とみなすとANDゲートの出力は入力に応じて以下のようになる

• これは入力の区別をなくすと以下のような表にまとめられる

AND	0	1
0	0	0
1	0	1

ORゲート

• 次に並列につながれた2つのリレーを見てみよう

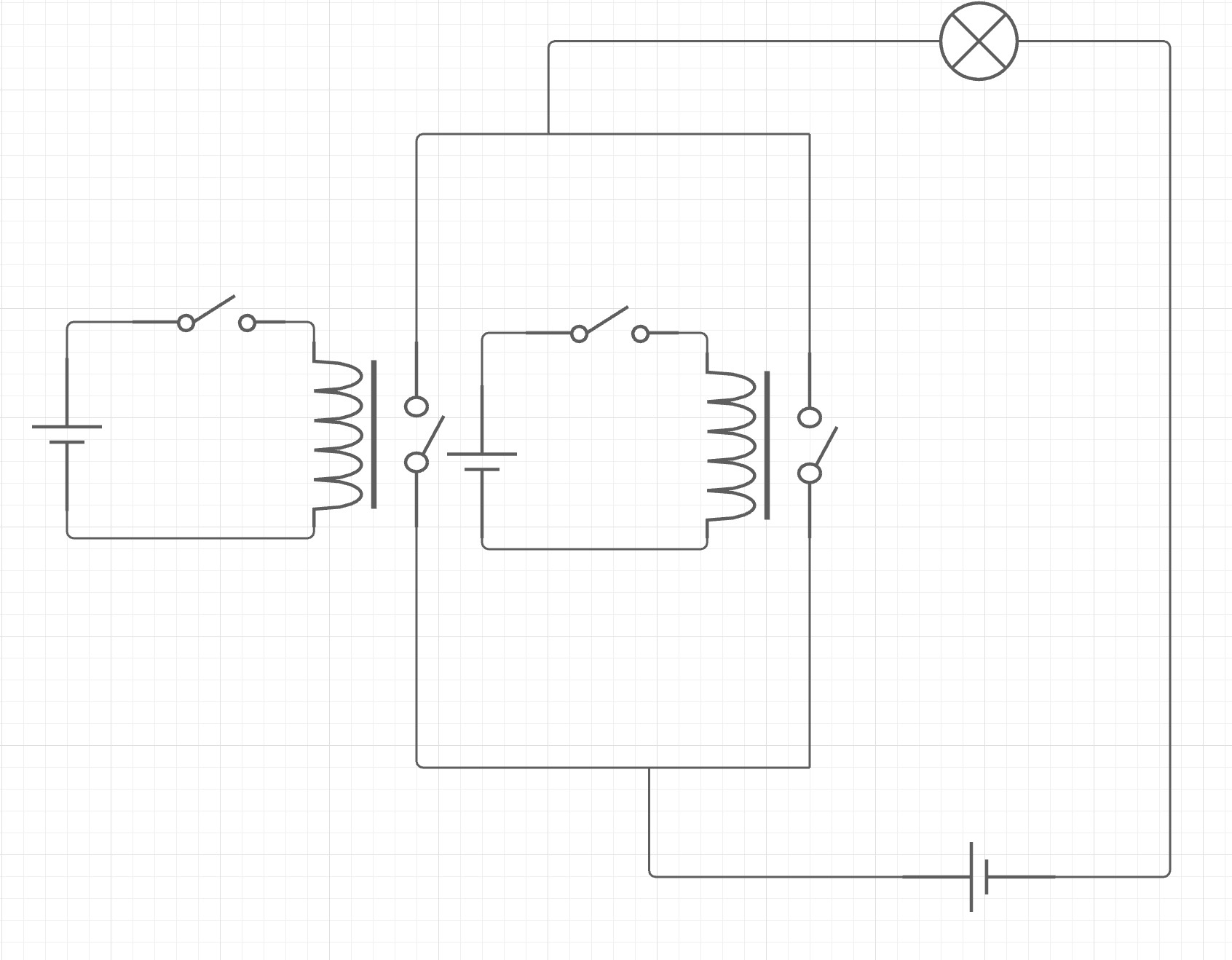
• この2つのリレーではそれぞれの出力が互いに接続されていることがポイントで、接続された出力は電球に電圧を供給している。

• そしてこの電球を点灯させるにはどちらかひとつのリレーが起動すれば充分であり、例えば左のスイッチを閉じれば左のリレーから電圧が生じて、点灯する

• つまり、前章で見た並列回路と同じで、この電球は**「どちらかのスイッチが閉じているか？」という問いに対しての答えになっており、この並列につながれた2つのリレーをORゲート**と呼ぶ

• ORゲートは以下のような記号が用いられる

• これも左側が入力、右側が出力として描かれている

• ORゲートの出力は2つの入力のうちのどちらかが電圧を持てば電圧を供給できるようになるため、電圧の有無をビットに対応させると次のような簡単な表にまとめることができる

OR	0	1
0	0	0
1	0	1

インバータ

• リレーをこのように様々な方法で接続することで論理ゲートを作成できるが、実は単独のリレーでも出力を２通りに接続することができる

• 例えば以下のように接続すると、今までとは入出力の関係性が逆になり、スイッチを開くことで電球が点灯するようにできる

• このように出力を２通りに接続できるリレーを双投式リレーと呼ぶ

• そしてこのようにスイッチを開くと電圧が供給されるように配線された単一のリレーはインバータと呼ばれている。このインバータは論理ゲートではないが、様々な場面で登場する

• インバータの記号は以下のように表現される

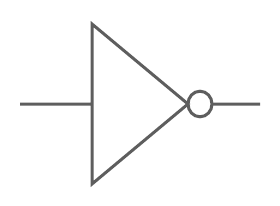
• このインバータの由来は**入力電圧を逆転（invert）させて出力電圧として出力するからである。**つまり、0（電圧なし）を1（電圧あり）に、1（電圧あり）を0（電圧なし）に変換するのである

2線-4線デコーダ

• ここまで見てきたインバータとANDゲート、ORゲートを用いて、先ほどのコントロールパネルの配線を試みてみる

• まずはスイッチを基準に考えていこう

• 「性別」と「去勢」に関しては簡単に作成できる。

• これらは以下のようにスイッチをひとつ用いた回路を作成できれば充分である。

• この回路では第1のスイッチはメスなら閉じてオスなら開くようになっている。そしてそれによりFとMという2つの信号を生成する

• つまりFが1の時Mは0になり、またその逆も成り立つ。

• 第2のスイッチに関しても同様である

• 次に「色」に関して考えてみる。これは2ビットの情報であるため、2つのスイッチを組み合わせることで4つの異なる色を示さなければならない

• まず2つのスイッチを両方とも電圧につないでみよう

• そして両方のスイッチが開いている時、白を示すようにゲートを組み合わせると以下のようになる

• この回路では白猫を選んだときに電圧あり（1）、選ばなかったときに電圧なし（0）となるようにしている

• 例えばどちらかひとつのスイッチがオンになったら白猫の信号は電圧なしとなるのでしっかりとこの条件を満たす

• 次に黒を示す回路の組み合わせを考えてみると以下のようになる

• 黒は上側のスイッチがオンの時のみとすると、上の回路が条件を満たしていることはわかるだろう

• 次に褐色について考えてみる

• 褐色は黒とは逆のスイッチがオンの時のみ出力が電圧あり（1）となるようにしなければならないので以下のような回路図となる

• 最後にそれ以外の色について考えてみる。
• これは両方のスイッチがオンになる時飲みに電圧ありとなるので、以下のような回路となる

• では材料が揃ったところで、これら4つの小さな回路を組み合わせてひとつの大きな回路にしよう

• ここで注意しておかなければいけないのは、ゲートやインバータのつなぎ方には簡単な規則が存在しているということ

• 具体的には

  • 1つのゲート（もしくはインバータ）の出力は1つまたは複数の他のゲート（もしくはインバータ）の入力になりうる
  • 一方、複数のゲート（あるいはインバータ）の出力は互いに接続してはいけない

• そしてこのANDゲート4個とインバータ2つからなる回路は、2線4線デコーダと呼ばれている

• 入力は二つのビットであり、その様々な組み合わせで4通りの異なる値を表すことが可能である

• 出力は4個の信号であり、2つの入力の値に依存して常にそのうち1つのみが1となる

• この仕組みを利用すると、3線-8線デコーダや4線-16線デコーダなどを作ることも可能になる

コントロールパネルの設計

• さてではこの2線-4線デコーダを用いて先程のコントロールパネルの内部設計を行うと以下のようになる

• ちなみに簡略された猫の選択式は次のようなものであった

• N × ((M × (W + F) + (F × (1 - W))) + B

• 回路図の左側の信号は、インバータにつながれたスイッチと2線-4線デコーダから来ている。
• この電球の点灯/非点灯により指定された猫を選んだかどうかの判断が可能になる

NORゲート

• 次に残りの2つの論理ゲートを見ていく

• これらのゲートは両方とも、起動されていない時に電圧があるリレーの出力を使用している（インバータに用いられていた出力方法とイメージすれば良い）

• たとえば以下のような2つのリレーを見てみよう

• この構成の場合、両方の入力がオフの場合に電球は点灯する

• そしてどちらか一方の入力がオンの場合には電灯は点灯しない

• この挙動はちょうどORゲートの反対であるためNOT ORまたは短縮してNORと呼ばれている

• 記号で表すと以下のようになる

• また入出力の関係は以下の表のようになる

NOR	0	1
0	1	0
1	0	0

NANDゲート

• また同様にANDゲートの逆のゲートも組むことができ、これはNOT ANDまたはNANDとも呼ばれている

• 入出力の関係は以下のようになっている

NAND	0	1
0	1	1
1	1	0

基本論理ゲート

• ここまで見てきた4つの論理ゲートは基本論理ゲートと呼ばれ、入出力の関係性をまとめると以下のようになる

AND	0	1
0	0	0
1	0	1

OR	0	1
0	0	1
1	1	1

NOR	0	1
0	1	0
1	0	0

NAND	0	1
0	1	1
1	1	0

ド・モルガンの法則

• さてここでANDゲート、ORゲートの入力部分を逆転させたゲートをそれぞれ考えてみよう

• これらの入出力を考えてみるとそれぞれ以下のような等価性があることに気づく

• ここですでに気づいた方はいるかもしれないが、これは実はド・モルガンの法則を電気的に実現させたものである
• ド・モルガンの法則は「論理と集合」と呼ばれる高校数学の分野で登場する法則であり、以下のような式で表される

• ここでこの集合AとBはプールオペランドを表しており、それぞれの演算子を論理演算子+と×に置き換えることができる

• すると先程の回路の等価性が成り立つことがわかるだろう

• つまり、歴史的に見ればクロード・シャノンの論文はド・モルガンの法則を証明したものであったことがわかる

• またこのド・モルガンの法則はプール式を単純にするため、回路の単純化にとっても非常に重要な道具となっている

12. 2進数加算器

コンピュータの基本は足し算

• コンピュータは足し算が最も基本的な機能

• そのため、コンピュータを作るにはまず2つの数を足すものを作る必要がある。足し算ができれば四則演算はもちろんありとあらゆる様々な機能を付与することができる

• ここから先はスイッチ、電球、同線、電池、リレーを接続して作った様々な論理ゲートだけを使って加算器を作る

• 道具は違えど基本的に現代のコンピュータでもやっていることは同じである

2進数の足し算

• 2進数の足し算は基本的には10進数の足し算と同じで、各桁同士で足し算を行うことにより計算が可能

• さらに2進数の各桁の足し算は非常に単純であり、以下のような表にまとめることができる。これは2進数は0と1しか用いないため、計算パターンが限られていることに由来している

+	0	1
0	00	01
1	01	10

• ここで各桁を**サムビット（和ビット）、キャリービット（繰り上げビットまたは桁上げビット）**と呼び、それぞれを分けると以下のような表が得られる

• このように表を分けるのは、私たちは一般的に和と繰り上げを別々に実行しているからであり、こうして見た方がわかりやすいからである。

+サム	0	1
0	0	1
1	1	0

+キャリー	0	1
0	0	0
1	0	1

• ここからは**8ビット**までの和に限定して考えてみよう

2進数加算器の作成①

• まずこの加算器のコントロールパネルの外観は以下のようになるであろう

• このパネルには8個ずつ2列のスイッチがあり、これらのスイッチが入力デバイスである

• これを使って2つの８ビット数を入力する

• さらにパネル下部の出力デバイスは1列に並んだ9個の電球である。これらの電球が答えを表示する。

• 消えている電球は0、点灯している電球は1である

• 9個の電球が必要となるのは2つの8ビット数の和が9ビット数になりうるからである

2進数加算器の作成②

• この加算器の内部は多数の論理ゲートを様々に繋いだものとなっている

• スイッチが論理ゲートのリレーを起動し、それが正しい電球をオンにする

• ここで先程のキャリービットの表を思い出して欲しい

+キャリー	0	1
0	0	0
1	0	1

• この表を見たとき論理ゲートとの関連性に気付いた人は多いかもしれない

AND	0	1
0	0	0
1	0	1

• ここからANDゲートは2つの2進数字の足し算のキャリービットを計算することがわかる

• 次はサムビットについて見てみよう

+サム	0	1
0	0	1
1	1	0

• これに全く等しい論理ゲートはないが、似ている論理ゲートとしてORゲートとNANDゲートが存在する

OR	0	1
0	0	1
1	1	1

NAND	0	1
0	1	1
1	1	0

• これら2つを同じ入力に繋いでみよう

• 次の表は、ORゲートとNANDゲートの出力をまとめて加算器に必要なものと比較してみた結果である

入力A	入力B	OR出力	NAND出力	必要な結果
0	0	0	1	0
0	1	1	1	1
1	0	1	1	1
1	1	1	0	0

• ここから必要な結果が1になるのは、ORゲートとNANDゲートの出力が同時に1になるときだけであることがわかる

• これから以下のような論理ゲートの組み合わせによりサムビットが得られることがわかる

• 実はこの回路には名前が付いており、排他的ORゲートまたはXORゲートと呼ばれており、以下のような記号が用いられる

2進数加算機の作成③

• ここまでをまとめると以下のような2つの2進数字の足し算を表す回路を得ることができる

• これは単に次のようなボックスを書くことにより表現できる

• この装置は**「半加算器」**と呼ばれている。ここで「半」と呼ばれているのには理由がある

• 確かにこの加算器は2つの2進数字を加えてサムビットとキャリービットを出すが、ほとんどの2進数は1ビットより長いことが多い。

• ここで半加算器が行えないことは前の桁の足し算からのキャリービットを加えることである

• たとえば 1111 + 1111などのような足し算を実行する場合、半加算器が使えるのは1番右の桁だけである

• 右から2番目の桁などには繰り上げが存在するため、理論上3つの数を足し合わせる必要があり、これ以降の数についても同様である

• この問題を解決する装置が以下のような回路である

• この図を理解するにはまず左の最初の半加算器への入力AとBから始める

• 出力はサムとキャリーであり、そのサムには前の桁からのキャリーが足されなければならないので、これらが第2の半加算器への入力になる

• 第2の半加算器からのサムが最終のサムである

• また2つの半加算器からの2つのキャリーアウトは、ORゲートへの入力である

• ここでもうひとつ半加算器が必要になるかもしれないと多くの人は思うが、実際は必要ない

• というのも、全ての可能性を考えてみると、2つの半加算器からのキャリーアウトが同時に1になることはあり得ないからである

• したがって、これらを加えるにはORゲートで十分であり、入力が同時に1にならないのならばORゲート=XORゲートである

• そしてこれも記号で書くと以下のようになり、これは全加算器と呼ばれる

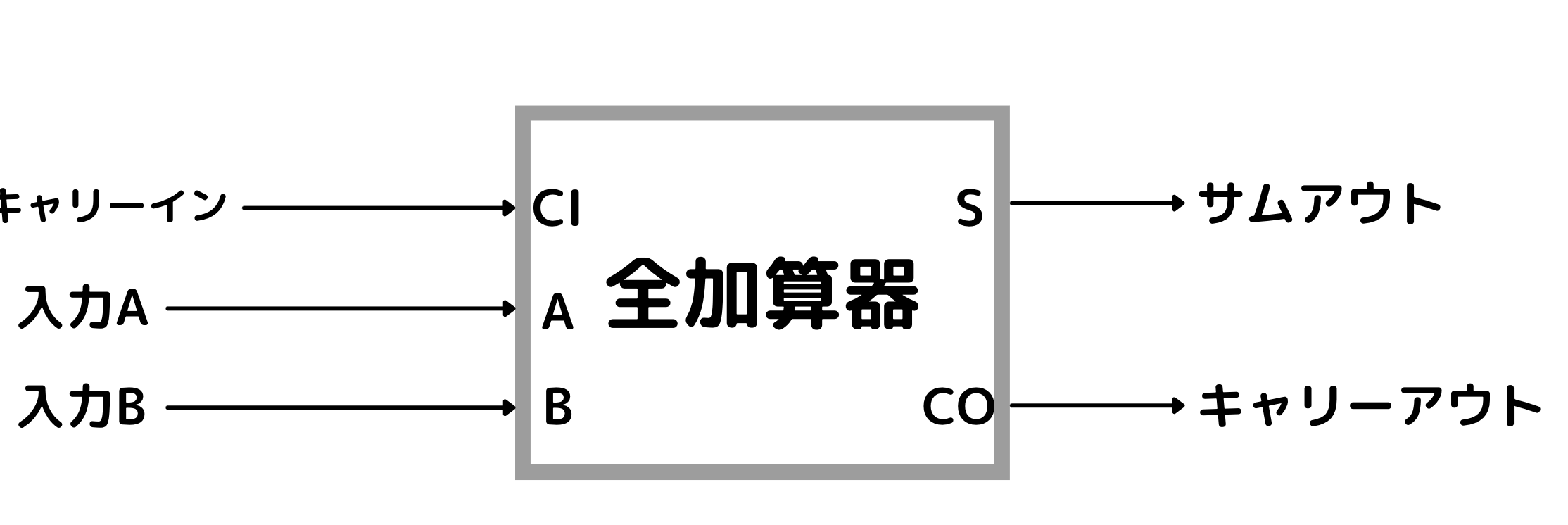
2進数加算器の作成④

• さて先程のコントロールパネルにはスイッチと電球が付いていたので、このスイッチと電球を全加算器に付けてみると以下のようになる
• ちなみにこれは1番右のスイッチと１番右の電球を繋いだもの

• 2つの2進数の足し算を始める1桁目は特別な桁となっていて、キャリーインが０になっている。（これは1桁目はキャリービットを含まないため）

• そして1桁目の足し算は当然繰り上げを生じることがあり、そのキャリーアウトは次の桁へのキャリーインとなっている

• 次の桁の2つの数と電球に全加算器は以下のようにつなぐ

• 最初の全加算器からのキャリーアウトはキャリーインへと繋がれ、その次に現れる各桁も同様に配線されている

• 各桁のキャリーアウトは次の桁への入力になっている

• 最後に8番目のスイッチ2つが最後の全加算器へと繋がれる

• 最後のキャリーアウトは9番目の電球に流れていく

• これで完了であり、8個の全加算器の組み合わせを書くと以下のようになる

• この8ビット加算器全体を1つのボックスとして描いたものが次の図である

• 入力にはA0からA7およびB0からB7までのラベルが付けられており、出力にはS０からS7までのラベルが付けられている

• これは複数ビットの数に現れる個々のビットにラベルをつける一般的な方法である

• ビットA0、B0、S0は最下位ビットまたは右端ビットと呼ばれている

• ビットA7、B7、S7は最上位ビットまたは左端ビットと呼ばれている

• 次の例ではこれらの添字付き文字と2進数0110-1001との対応を示している

A7	A6	A5	A4	A3	A2	A1	A0
0	1	1	0	1	0	0	1

• 下付き文字は0から始まり、位が上がるについれて大きくなる、これらは2の累乗の指数に対応している

• またこれらの8ビット加算器の別の書き方は以下のようになる

• 矢印の中の8は、それぞれが8つの別々の信号の集まりであることを示している

• それらにはA7...A0、B7...B0、S7...S0というラベルも付いていて、8ビットの数であることを示している

• またここからもうひとつ8ビット加算器を作り、それをカスケードにして簡単に2つの16ビット数を足すことも可能である

• これは右の加算器のキャリーアウトは左の加算器のキャリーインに接続されていて、左の加算器は加えるべき2つの数の上位8桁を入力として持ち、出力として上位８桁を作っている

現在のコンピュータはどうなっているの？

• さてここまで読んでくると、「現在のコンピュータ内部の計算の仕組みもこのようなものとなっているのか？」という疑問を持つ人も多いだろう

• 結論から言うと基本的にはそうであるが、「中身の仕組み」などが少々違っている

• たとえば、現在のコンピュータでは加算器はこれよりも高速に動作するように作られている

• 現在の加算器の場合、前の桁のキャリーアウトが計算したい桁のキャリーインに繋がっており、加算器全体の速度が「ビット数×全加算器」に依存することを表している

• このような加算器はリップルキャリーと呼ばれており、現在のようなより高速化した加算器にはルックアヘッドキャリーと呼ばれる追加の回路が用い垂れている

• また現在のコンピュータではリレーはそもそも使われていない

• 現在はご存知のようにトランジスタが用いられている

• トランジスタは基本的にはリレーと同等に機能するが、もっと速いく小さくさらに消費電力が小さいし、安いのである

13. でも引き算はどうする？

通常の足し算と引き算

• ここまで足し算を見てきたが、では引き算はどのように論理ゲートを組めば良いだろうか？

• まず一般的な足し算と引き算の違いをおさらいしておこう

• 足し算は右の桁から左の桁へ「桁上げ」を行いながら計算を実行する一方、引き算の場合は**「桁借り」**を行って計算を実行する

• たとえば253 - 176の場合を考えてみる

• この場合当然一番右の桁から計算を始めて、3は6より小さいため5から1を借りて、13から6を引くことにする。計算結果は7となる

• 次の桁は5から1を借りたので4になり、4は7より小さいので2から1を借りて、14から7を引くことにする。すると結果は7となる

• 最後の桁は2から1を借りたので1になり、そこから1を引いて0になる。

• つまり答えは77である

引き算の別の方法①

• しかし、引き算は実はこのようにわざわざ桁借りをする必要がない

• では桁借りをせずにどのように引き算を行えば良いのだろうか？

• この方法を考える前にまず引き算で用いる2つの数について言及する必要がある

• 引き算で用いられる数は被減数、減数と呼ばれる

• 被減数ー減数＝差

• 先程の例で言うと、被減数＝253、減数＝176

• そして桁借りをしないようにする場合、このまま被減数ー減数をしてしまうといけない

• 代わりにまず減数を被減数からではなく、999から引くことにする

• 999 - 176 = 823

• こうすることで桁借りをする必要がなくなる

• そしてこのようにある数を一連の9から引くと、結果は9の補数と呼ばれる数になる（先の例では補数＝823）

• 9の補数を用いるのは、たとえ減数がどのような場合であっても計算に桁借りをする必要はないからである

• そして減数の9の補数を計算したら、次は元の被減数にそれを加える

• 253 + 823 = 1076

• そして最後に1を加えて1000を引く

• 1076 + 1 - 1000 = 77

• 最終結果は以前と同じだが、一度も桁借りをする必要はない

引き算の別の方法②

• ではなぜこのような方法が成り立つのだろうか？

• まず先程の引き算を以下のように変形する

• 253 - 176 + 1000 - 1000

• そしてさらに次のように変形する

• 253 - 176 + 999 + 1 - 1000

• 253 + (999 - 176) + 1 - 1000

• そしてこれは9の補数を使用して示した計算と一致している

• このように1回の引き算を2回の引き算と足し算で置き換えることで桁借りを全てなくせる

引き算の別の方法③

• では先程の被減数と減数を入れ替えてみるとどのようになるだろうか？

• まず先程と同様に減数の9の補数を考えてみると以下のようになる

• 999 - 253 = 746

• そしてこの9の補数を元々の被減数に加える

• 176 + 746 = 922

• 前の計算では、この時点で1を加えて1000を引けば計算結果が得られたが、今回の場合は同じ方法ではうまくいかない

• というのも923から1000を引く必要が生じ、この場合は1000から923を引くことを意味するので、桁借りが必要となってしまう

• そのため今回は999を引くことにする

• 923 - 999は実質的には999 - 923をすることと変わりないので結果は-77となるのがわかる

引き算の別の方法④

• このように桁借りをせずに引き算をする方法を紹介してきたが、これは基準をずらすイメージを持つとわかりやすいだろう

• つまり、負の数を考える場合0を基準にするのではなく、1000もしくは999を基準にして必ず正の数として考えられるようにするということである

• たとえば1つ目の例の場合、-176を999を基準として考えた場合、999 - 176 = 823となる

• これにさらに1を加えて、824とし1000が基準点になるようにずらす

• これに253を加えると、1077となる

• そして最後に基準点を元の0に戻す。今回は1000が基準点だったので、1077から1000を引き、77が答えとなる

• また2つ目の例の場合、-253をまずずらす。先ほどと同様に999を基準点にすると、-253は746となる

• これに176を加えると、922となる

• ここで先程は1000を基準点とするため1を加えたが、今回は1000を基準点とすると最後に引き算をする場合に桁借りをする必要が出てくるので1を加える必要性はない

• 最後に基準点を0にずらせば終了。今回は999を引くのだが、負の数となるため999から922を引き、最後に符号を逆転させることで計算を行う

• このように補数を考える際は**「基準点の移動」**をイメージしながら考えていくとわかりやすいだろう（あるいは数直線を実際に書いて考えるのもおすすめ）

2進法での引き算

• 今まで見てきた方法は2進数にも適用が可能である

• 先の例の253 - 176を2進法に変換すると、以下のようになる

• 11111101 - 10110000

• ここでも最初に10110000を11111111から引くと11111111 - 10110000 = 01001111となる

• 2進数では減数を1の列から引くと結果は1の補数と呼ばれているものとなる

• ここでは1の補数を求める際、実際に引き算を行って求めたが、よく考えればわざわざ引き算を行う必要はない

• というのも、2進数には0か1しかなく、0は1の補数では1となり、1は1の補数では0となる。つまり、1の補数を考える際は0と1を入れ替えるだけで良いのである

• このような性質から1の補数は否定もしくは反転と呼ばれる

• 計算の続きに移ると、次は減数の1の補数を被減数に加える

• ここでは11111101 + 01001111 = 101001100となり、さらに1を加えると101001101となる

• ここから基準点を0に戻すと、今回は1を加えているので100000000を引くことになる

• つまり、101001101 - 100000000 = 1001101（10進法では77）となる

• 被減数と減数を入れ替えても同様である

加算器の改良①

• さてこれで12章で作った加算器を変更して足し算だけでなく引き算もできるようにするための知識も得られた。

• ということでここからは**被減数よりも減数が小さい（つまり答えが正になる場合）**に限定して、引き算を実行できるような装置を作っていこう

• まず加算器の中核は論理ゲートから組み立てられた8ビット加算器であった

• そしてコントローラの外観は以下のようであった

• 引き算も実行したい場合はこのコントロールパネルに少し変更を加えなければならない

• それはまずは足し算と引き算のどちらかを選択するスイッチの追加である

• ラベルが示しているようにこのスイッチをオフにすると足し算、オンにすると引き算である

• また右から8個の電球だけが結果の表示に使われ9番目の電球には**「Overflow/Underflow」**というラベルが付き、8個の電球では表示できない数が計算されていることを示す

• これが起きるのは足し算が255より大きい数を生じる場合（オーバーフロー）と、引き算が負の数を生じる場合（アンダーフロー）である

• 引き算が負の数を生じるのは減数が被減数より大きい場合である

加算器の改良②

• さてここからは中核にあたる論理ゲートの変更を見ていこう

• まず8ビット数の1の補数を計算する回路を追加する必要がある

• 1の補数はビットの反転に等しいので、その回路は単に8個のインバータに近そうである

• しかし、これだと入ってくるビットを常に反転させてしまう。

• 我々は足し算と引き算の両方に対応する機械を作ろうとしているので回路は引き算の時だけビットを反転する必要がある

• このため、次のような回路の方が適している

• **「反転」というラベルからの単一の信号は、8個のXOR（排他的OR）ゲートのそれぞれへの入力である。**XORの挙動は次のようなものであった

XOR	0	1
0	0	1
1	1	0

• ここからもし反転信号が1ならば、XORゲートの8個の出力は8個の入力と同じであるし、また反転信号が1なら8個の入力信号は反転されることがわかる

• これら8つのXORゲートを1つのボックスに入れて「1の補数」というラベルを付けよう

加算器の改良③

• ここまでで1の補数ボックス、8ビット加算器ボックス、そして最後のXORゲートを次のようにつなげば一応ほとんど引き算付き加算器の完成である

• 装置の中身を詳しく見ていこう

• まず「SUB」というラベルの信号が3つあることに着目してみよう

• これは加減スイッチであり、足し算のときは0、引き算のときは1である。

• 引き算の場合、入力Bは加算器に入る前に1の補数回路によって全て反転される。さらに引き算の場合は、加算器のCI（キャリーイン）入力を1に設定することによって足し算の結果に1を加える

• 足し算の場合は1の補数回路に影響されることはないため、CIは0になる

• 少しややこしいのが、Overflow/Underflowランプの点灯に使われる論理ゲートである

• この部分では、SUB信号と加算器のCO出力がXORゲートの入力となっている。これはどういうことだろうか？

• まず、足し算が実行されている場合SUB信号が０になるため、CO出力が1のときに点灯する

• つまり、足し算の結果が255より大きいということを意味している

• では引き算が実行されていてSUB信号が1の時はどうだろう？

• 今回は減数（スイッチB）が被減数（スイッチA）より小さい場合であり、この時加算器からのCO出力は1になるのが正常である

• というのも、2進数の引き算の最後の段階で100000000を引いたことを思い出すと、CO出力が1以外は考えられないからである

• もしCO出力が0になってしまうと、それは引き算結果が負になることを意味し、Underflowランプが点灯することも納得がいくだろう

負の数の表し方（10進法）

• さてここまでで引き算を実行できるような加算器を設計してきたが、そもそも負の数は2進法でどのように表せるのだろうか？

• ひとつの方法はマイナスの符号をそのまま用いることだが、今回はそれを抜きにして考えていきたい。というのも2進法で考えるメリットはすべての情報を0と1で表すことであり、マイナス符号も0と1で表すべきだからである

• ひとつの方法としては符号用にビットを用いることである

• たとえば負の数を表したいときは先頭に1を置き、正の数を表したい時は0を置くようにする

• もちろんこれでもうまくいくが、実は「特定の範囲内にある数だけを扱いたい」という場合に限ると、他にもっとうまい方法が存在している。これについて今回は考えていこう

• まず私たちが通常使っている方法で正負の数を書くことの利点は、どこまでも続けることができるという点である

• 私たちは0を中心にして正の数の列が一方向に無限に続き、負の数の列がもう一方向に無限に続くものだと思っている

...-1,000,000 -999,999 ... -3 -2 -1 0 1 2 3 ... 999,999 1,000,000 ...

• しかし、状況によっては無限大も数は必要ないとなる可能性もある。つまりあらかじめ遭遇する数の範囲が決まっているということも少なくはないだろう。

• そのような場合には負の数をわざわざ使うことなく全ての数を表すことができる

• たとえば私たちが-500から499までの1000個の数しか使わないとしよう

• この際私たちは3桁の10進数だけを用いて全ての数を表すことが可能である。

• というのも、3桁の範囲内において500から999までの正の数が必要ないからである。我々は先ほど必要な最大の正の数は499と決めたからである

• このため500から999までの3桁の数は負の数を表すために用いることができるのである。その対応関係は以下の通りになる

	対応する数
-500	500
-499	501
-498	502
...
-2	998
-1	999
0	000
1	001
2	002
...
497	497
498	498
499	499

• 言い換えれば5,6,7,8または9で始まる3桁の数は、実際には負の数なのである

• つまり数が下のように並んでいるイメージである

500 501 502 ... 996 997 998 999 000 001 002 003 004 ... 497 498 499

• この形式は一種のサイクルである。最低の負の数（500）はあたかも最高の正の数（499）から続いているように見える。

• さらに999（実際には-1）は0より1小さい。999に1を足すと普通は1000だが、3桁の数だけを扱っているので実際は000になる

• この種の記数法は10の補数と呼ばれている。

• 実際に3桁の負の数を10の歩数に変換するには、それを999から引いて1を加える。

• 　言い換えれば9の補数に1を加えたものが10補数になる

• 　他にもたとえば-255を10の補数とするには、999から引いて744、それに1を加えた745が答えである

• そしてこの記数法を用いれば引き算は存在しなくなり、全てが足し算になるのである

• たとえば300に-255を足すことを考えよう

• -255は先ほど計算した通り、10の補数で表すと745になる

• これに300を足すと1045となり、オーバーフローを無視すると45となる

• これは実際に引き算を行った結果とも合致する

負の数の表し方（2進法）

• 先ほどの10の補数は2進法では2の補数と呼ばれる

• 私たちは8ビットの数を扱っているとしよう

• これらの範囲は00000000から11111111までであり、通常は10進数の0から255までに対応している

• しかし、負の数も現したいなら次の数に示されているように、1で始まる各8ビット数を用いることになるであろう

2進数	10進数
10000000	-128
10000001	-127
10000010	-126
10000011	-125
...	...
111111101	-3
111111110	-2
111111111	-1
00000000	0
00000001	1
00000010	2
...	...
011111100	124
011111101	125
011111110	126
011111111	127

• これで表される数の範囲は-128から127までの256個の数である

• そして最上位のビットは符号ビットとして知られている。符号ビットが1なら負の数、0なら正の数である

• この2の補数を計算するには、10の補数と同様にまず1の補数を計算してから1を足せば良い

• しかし10の補数と違うのは、わざわざ計算する必要がないということだ

• 先ほど説明した通り、1の補数は反転すれば良いだけなので、2の補数は全桁を反転させて1を加えるだけで簡単に求めることが可能である

• たとえば10進数125は01111101である。-125を2の補数で表すには、まず01111101の各桁を反転して10000010を得て、それに1を加え、10000011という2の補数を得る。実際に先程の表を見ても正しいことがわかる

• さて、ではこの体系を用いて引き算を計算してみよう

• たとえば-127と124の2進数を足してみよう

• 前の表を用いると、これは次のものであることがわかる

• 10000001 + 01111100 = 11111101

• これは10進数でいうところの−３であることがわかる

オーバーフローとアンダーフロー

• しかしこの計算で唯一注意しなければならないことはオーバーフローとアンダーフローの状態である

• それは8ビット範囲では足し算の結果が127より大きいとき、あるいは-128より小さい時に生じる

• たとえば125に125を足すとしよう

符号	数
	01111101
+	01111101
----	---------------
	11111010

• これは最上位ビットが1なので、負の数として解釈することになるが、実際の計算結果は違っている

• また同様に-125に-125を足すときにもこの現象は生じる

符号	数
	10000011
+	10000011
----	---------------
1	00000110

• これは8ビットを超えているため、最上位ビットを無視すると結果は正の数として解釈することになる

• このように正と負の数を足し算を扱う場合、2つのオペランドの符号ビットが同じで結果の符号ビットが異なっていた場合結果は無効になる

ビットの難点

• このようにビットには2通りの表し方があることがわかった

• つまり、ビットは符号付きもしくは符号なしのどちらかであるということ

• 符号付きの8ビット数は-128から127までで、符号なしの8ビット数は0から255までである

• ここで重要なのが数自体は符号付きか符号なしかを語らないということである

• これがビットの難点であり、利点でもある。

• ビットは単なる0と1に過ぎず、ビットで表された情報というのは0と1の羅列でしかない。ビット自体は自分自身について何も語らないのである

-1. つづく

• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ①

• [初心者]CODE 〜コードから見たコンピュータのからくり〜 ③・・・（現在執筆中）

• • [初心者]CODE 〜コードから見たコンピュータのからくり〜 ④・・・（現在執筆中）