本記事は第二のドワンゴ Advent Calendar 2019の22日目の記事です。
はじめに
ドワンゴの企画職として、ニコニコ生放送サービスや配信ソフトウェアN Airに携わっています。
SlackでAdvent Calenderについてエンジニアの方々が盛り上がっているのを見て、自分も参加してみたくなりました。担当した施策の簡単な分析や生放送事業のKPI管理を行っているので、この機会に数値分析周りの記事を書いてみようと思います。
生主の配信継続期間
ニコニコ生放送はユーザーが自由にライブ配信できるプラットフォームです。料理をしながら雑談をしていたり、ゲームを実況していたり、マイナーな音楽を紹介していたりと、各々の生主が気ままに自分のスタイルで放送を楽しんでいて、個人的にも大好きなサービスです。
運営としては多くの生主にできる限り長く配信を続けて楽しんでもらいたいものです。では一体生主はどの程度の期間継続して配信するものなのでしょうか。以下ではこの「配信継続期間」の集計と分析に挑戦してみます。
平均継続期間の求め方
基本方針として、生主の翌月継続率からnヶ月間継続して配信する確率を求め、平均的な継続期間を導出します。
ある月の生主の数を $N$ として、その月に配信を行なった生主に対して
- 翌月にも配信を行なった場合は $X_i=1$
- 翌月に配信を行わなかった場合は $X_i=0$
となるように継続の真偽を表す確率変数 $X_{i}$ を用意します。ここでiは1以上N以下の整数です。このとき、翌月継続率 $P$ は
$$P=\frac{\Sigma_{i=1}^{N} X_{i}}{N}$$
で表されます。
ここで1点注意です。配信を始めたばかりでは機材の調整が難しかったり、視聴者が思ったように集まらなかったりして、生主として軌道に乗るまでに離脱してしまいやすい傾向にあります。したがって、新規の生主は既存の生主に比べて継続率が低くなります。この事情を加味して、新規生主と既存生主で分けて扱うことにしましょう:
\begin{eqnarray}
P_{\text{new}}&=&\frac{\Sigma_{i=1}^{N_{\text{new}}} X_{i}}{N_{\text{new}}}\\
P_{\text{con}}&=&\frac{\Sigma_{i=1}^{N_{\text{con}}} X_{i}}{N_{\text{con}}}
\end{eqnarray}
ここで用意した $P_{\text{new}}$ 、$P_{\text{con}}$ を用いると、nヶ月目まで継続して配信し、n+1ヶ月目に離脱する確率は下記のようになります:
\begin{eqnarray}
\text{1ヶ月}&:&1-P_{\text{new}} \\
\text{2ヶ月}&:&P_{\text{new}}(1-P_{\text{con}}) \\
\text{3ヶ月}&:&P_{\text{new}}P_{\text{con}}(1-P_{\text{con}}) \\
\text{4ヶ月}&:&P_{\text{new}}{P_{\text{con}}}^2(1-P_{\text{con}}) \\
...&& \\
\text{nヶ月(n}\geq 2\text{)}&:&P_{\text{new}}{P_{\text{con}}}^{n-2}(1-P_{\text{con}})
\end{eqnarray}
この確率分布から残存数を計算することができます。SQLで継続期間を集計してみる の項で例として与えられるPCでの継続率 $P_{\text{new}} = 0.4223$、 $P_{\text{con}} = 0.6319$ を用いて、2019年9月に100人の新規生主がいたとして、その後の経過を求めてみると、次のグラフのようになります:
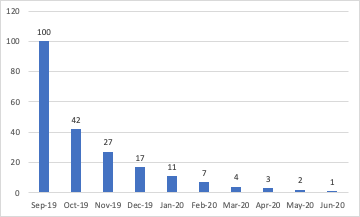
この継続率の設定だと2020年6月に1人になってしまうことが分かります。(実際は既存の生主や各月の新規生主が存在するためサービスは維持されます)
この確率分布を元に継続月数の平均値を求めていきましょう。平均継続月数は $P_{\text{new}}$ と $P_{\text{con}}$ の2変数関数なので $f(P_{\text{new}},P_{\text{con}})$ と表記すると、
\begin{eqnarray}
f(P_{\text{new}},P_{\text{con}}) &=& (1-P_{\text{new}}) + \Sigma_{n\geq 2}nP_{\text{new}}{P_{\text{con}}}^{n-2}(1-P_{\text{con}}) \\
&=& (1-P_{\text{new}})+P_{\text{new}}(1-P_{\text{con}})\left(\Sigma_{n\geq 0}n{P_{\text{con}}}^{n-2}-{P_{\text{con}}}^{-1}\right) \\
&=& (1-P_{\text{new}})+\frac{P_{\text{new}}(1-P_{\text{con}})}{P_{\text{con}}}(\Sigma_{n\geq 0}n{P_{\text{con}}}^{n-1}-1) \\
&=& (1-P_{\text{new}})+\frac{P_{\text{new}}}{P_{\text{con}}}\left(\frac{1}{1-P_{\text{con}}}-(1-P_{\text{con}})\right) \\
&=& 1+\frac{P_{\text{new}}}{1-P_{\text{con}}}
\end{eqnarray}
ここで3行目から4行目は
\begin{eqnarray}
\Sigma_{n\geq 0}n{P_{\text{con}}}^{n-1} &=& \Sigma_{n\geq 0}\frac{d}{dP_{\text{con}}}{P_{\text{con}}}^{n}=\frac{d}{dP_{\text{con}}}\Sigma_{n\geq 0}{P_{\text{con}}}^{n} \\
&=&\frac{d}{dP_{\text{con}}}\frac{1}{1-P_{\text{con}}}=\frac{1}{(1-P_{\text{con}})^2}
\end{eqnarray}
という式変形を行なっています。
以上より、新規生主、既存生主各々で翌月の継続率を求めることができれば、平均継続月数 $f$ を算出できるようになりました。この平均継続月数 $f$ をより深く理解するために、新規継続率のパターン別に眺めてみます。
1.新規生主が1人も翌月配信しない場合
$P_{\text{new}}=0$ なので平均継続月数 $f$ は1となります。全員が配信開始月以降配信を行なっていない状況を表しているので、平均を取っても継続期間は1ヶ月になります。
2.新規生主の継続率が既存生主の継続率と同じ場合
$P_{\text{new}}=P_{\text{con}}$ なので平均継続月数は $\frac{1}{1-P_{\text{con}}}$ となります。これは成功確率$1-P_{\text{con}}$の幾何分布の期待値そのものです。
このことから、上でわざわざ新規と既存に分けた意味を汲み取ってみましょう。今、平均継続月数 $f$ は
\begin{eqnarray}
f(P_{\text{new}},P_{\text{con}}) = \frac{1}{1-P_{\text{con}}} + \frac{P_{\text{new}}-P_{\text{con}}}{1-P_{\text{con}}}
\end{eqnarray}
とも書けます。この式を見ると第1項は新規と既存の継続率が同じときの平均継続期間になっているので、第2項は新規と既存の継続率の差が与える効果を表していることが分かります。この項は、新規継続率が既存継続率よりも大きい場合は平均継続期間も長くなり、逆に小さい場合は平均継続期間が短くなるように作用します。新規と既存の差を加味した補正項として、正しく機能していそうですね。
3.新規生主が全員翌月配信を行う場合
$P_{\text{new}}=1$ なので平均継続月数は $1+\frac{1}{1-P_{\text{con}}}$ となります。初配信の翌月も配信することが担保されており、それ以降の継続期間はパターン2と同じになります。余談ですが、この事実は本質的には幾何分布の無記憶性という性質に起因しています。
SQLで継続期間を集計してみる
では実際にデータから平均継続期間を集計してみましょう。新規・継続生主に対して各月における翌月配信率を求め、先ほどの公式を用いて集計します。
前提として、下のような放送月、生主の名前、配信デバイスが格納されたテーブル(テーブル名を「caster」とします)があるとします。分析を行う場合、全体の絶対値ではなく何らかのセグメントで分類して比較することが多いので、カテゴリーの例としてデバイス情報を付けています。また、通常はユーザー情報がユニーク化されたIDを使うのですが、分かりやすさのために生主の名前を用いています。
| month | user_name | device |
|---|---|---|
| … | … | … |
| 201909 | taro | iOS |
| 201909 | taro | PC |
| 201909 | hanako | Android |
| 201910 | jiro | PC |
| 201910 | hanako | PC |
| … | … | … |
最初のステップとして、このテーブルに各レコードが新規なのか継続なのかの情報を付与します。ここでは新規か継続かの情報はデバイスに依存しないものとして定義します。
WITH caster_2 AS (
SELECT
month,
user_name,
device,
if(
RANK() OVER (PARTITION BY user_name ORDER BY unix_timestamp(month, 'yyyyMM') ASC) != 1,
'continuous',
'new'
) AS type
FROM
caster
)
ここで新しく作った caster_2 というテーブルを出力すると次のような表になります:
| month | user_name | device | type |
|---|---|---|---|
| … | … | … | … |
| 201909 | taro | iOS | continuous |
| 201909 | taro | PC | continuous |
| 201909 | hanako | Android | new |
| 201910 | jiro | PC | new |
| 201910 | hanako | PC | continuous |
| … | … | … | … |
次にn月の配信情報とn+1月の配信情報を照合し、翌月配信を行なったかどうかの情報(is_repeatフラグ)を各レコードに付与します。デバイスの情報については各レコードの配信月に使用したものだけに着目し、翌月のデバイスは何でも良いとします。
,caster_3 AS (
SELECT
caster_2.month AS month,
caster_2.user_name AS user_name,
caster_2.device AS device,
caster_2.type AS type,
if(future.user_id IS NULL,FALSE,TRUE) AS is_repeat
FROM
caster_2
LEFT OUTER JOIN
(SELECT
DISTINCT
--n月とn+1月の情報を参照できるようにするため、未来の情報を1ヶ月過去にずらす
from_unixtime(unix_timestamp(add_months(from_unixtime(unix_timestamp(month, 'yyyyMM'), 'yyyy-MM-01'),-1),'yyyy-MM-dd'),'yyyyMM') AS month,
user_name
FROM
caster
) AS future
ON
future.month = caster_2.month
AND future.user_name = caster_2.user_name
)
from_unixtime(unix_timestamp(add_months(from_unixtime(unix_timestamp(month, 'yyyyMM'), 'yyyy-MM-01'),-1),'yyyy-MM-dd'),'yyyyMM')
この部分は month を1ヶ月過去にずらした月に変換しています。 add_months を使うために整形する都合上長くなってしまっています。
caster_3 というテーブルを出力すると、次の表のようになります:
| month | user_name | device | type | is_repeat |
|---|---|---|---|---|
| … | … | … | … | … |
| 201909 | taro | iOS | continuous | FALSE |
| 201909 | taro | PC | continuous | FALSE |
| 201909 | hanako | Android | new | TRUE |
| 201910 | jiro | PC | new | TRUE |
| 201910 | hanako | PC | continuous | FALSE |
| … | … | … | … | … |
最後にタイプ別、デバイス別の継続率を出力します。
SELECT
month,
device,
type,
COUNT(DISTINCT IF(is_repeat = 'TRUE',user_name,NULL)) / COUNT(DISTINCT user_name) AS ratio
FROM
caster_3
GROUP BY
month,
device,
type
;
出力結果は次の表のようになります:
| month | device | type | ratio |
|---|---|---|---|
| … | … | … | … |
| 201909 | PC | new | 0.4223… |
| 201909 | PC | continuous | 0.6319… |
| 201909 | iOS | new | 0.2141… |
| 201909 | iOS | continuous | 0.6424… |
| 201909 | Android | new | 0.4111… |
| 201909 | Android | continuous | 0.8502… |
| 201910 | PC | new | 0.2811… |
| 201910 | PC | continuous | 0.7502… |
| … | … | … | … |
サービスの実際の数値を公開することはできないので、ダミーの数値を入れています。
これらの値から各デバイスごとに各月の継続率から平均継続期間を計算してみましょう。2019年9月の数値を元に算出した平均継続期間は次のようになります:
| | PC | iOS | Android |
|---|---|---|---|
| 新規の翌月継続率 | 0.4223… | 0.2141… | 0.4111… |
| 既存の翌月継続率 | 0.6319… | 0.6424… | 0.8502… |
| 平均継続月数 | 2.1472… | 1.5987… | 3.7443… |
デバイス間で比較をしてみましょう:
-
PCとiOSの比較
- 既存の翌月継続率は同じ程度ですが、新規の翌月継続率は20%近く差があります。これにより平均継続月数は0.5ヶ月ほどiOSの方が短くなっています。
-
PCとAndroidの比較
- 新規の翌月継続率は同じ程度ですが、既存の翌月継続率は22%程度の差があります。これにより平均継続月数は1.6ヶ月ほどAndroidの方が長くなっています。
この2つの比較により、同じ20%程度の差でも、それが新規継続率か、既存のそれかで平均継続月数に与える影響は異なることが分かります。もう少し詳細に見るために、平均継続月数 $f$ のプロット図を眺めてみましょう。
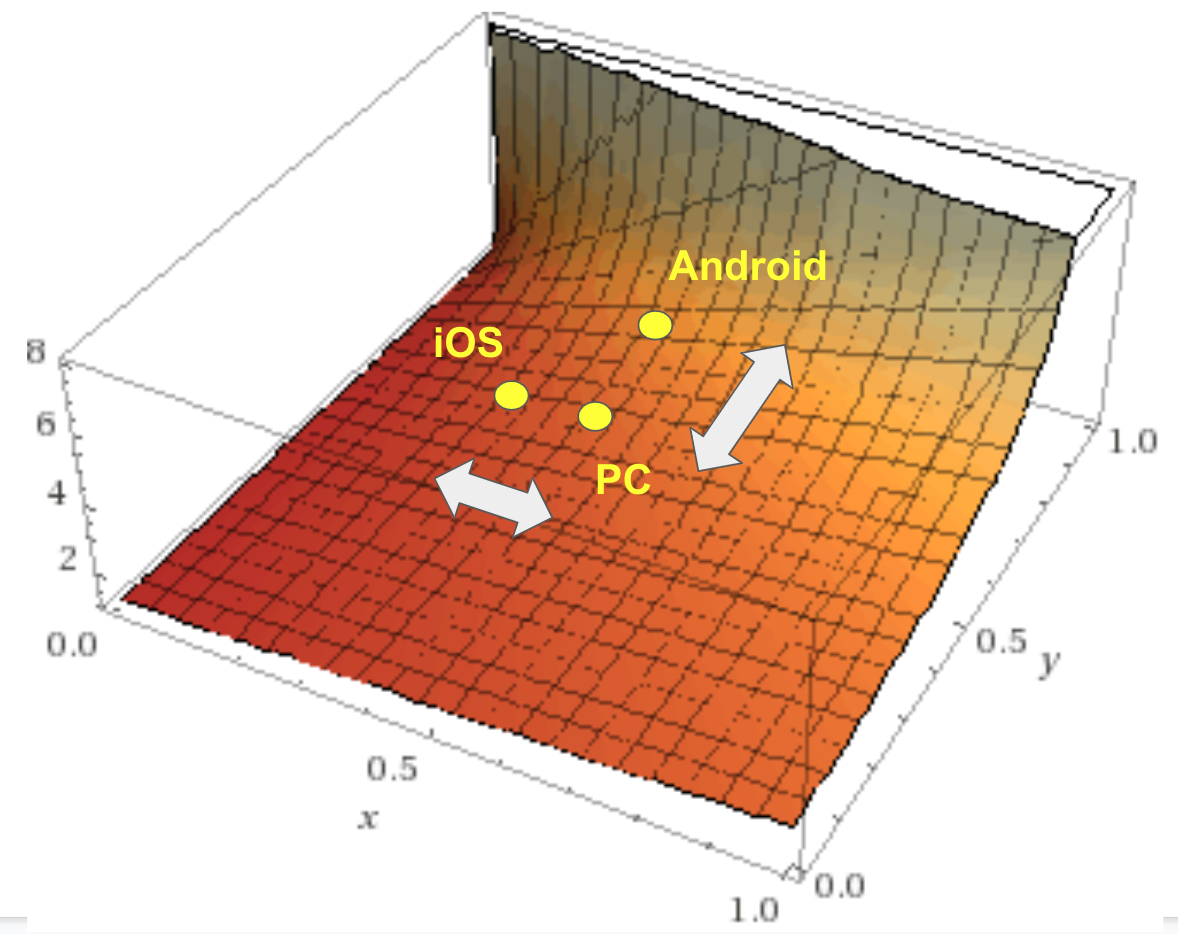
$x$ 軸が新規継続率、$y$ 軸が既存継続率を表します。各々、定義域は0以上1以下です。
既存の翌月継続率 $y$ が0.6のあたりを見ると、新規継続率 $x$ が0.2から0.4まで増えたとしても、そこまで平均継続期間は増えなさそうです。一方で新規継続率 $x$が0.4あたりを見ると、既存継続率 $y$ が0.6から0.8に増えると平均継続期間も大きく増えていく(勾配が大きくなっている)ように見えます。上で見た平均継続月数の上がり幅の差は、各値によって関数の傾きが異なることに起因する、ということが分かりました。
したがって、あるセグメント(ここではデバイス)の平均継続期間を長くする施策を考えるとき、新規・既存各々の継続率を見て、どちらに注力すると(もしくは両方にどのような配分で注力すると)最も効果的かを調べることが重要です。
上の内容はLTV(Life Time Value)の集計にも利用できます。特に月額定額サービスにおける各ユーザーのLTVは
\text{LTV} = \text{平均継続期間} \times \text{顧客単価}
で計算できるので、LTVを求めることは実質的に平均継続期間を算出することに帰結します。
おわりに
QiitaはSQLの知識を拾うのに記事を度々閲覧しているのですが、実際に記事を書くのは初めてでした。Texが書けることに感動しました。メモ書き程度に雑に残していた内容をまとめ直してみて、理解が浅い箇所が浮き彫りになったり、思考の整理になったり、非常に有益な体験でした。ぜひ来年も参加してみたいな、と思いました。
皆さま、良いお年をお過ごしください。