はじめに
先日ゼミで福水健次先生のカーネル法入門の3章までを読みました。ゼミでは手書きだったので発表資料のまとめ直しと、カーネル法の簡単な紹介をできたらと思います。(細かい理論は置いといて、)最後にカーネル主成分分析をpythonで実装します。私の発表範囲が前半の正定値カーネルと最後の実装の部分だったので、途中大きく抜けてるところがありますが大きな問題はないと思います。
注意
・理論よりも雰囲気を重視します。
・番号がついてるものに関しては福水先生の本の番号と同じです。
前提知識
・簡単な統計
・線形代数
・関数解析(ヒルベルト空間論)
目次
・カーネル法の概要
・正定値カーネル
・再生核ヒルベルト空間
・カーネル主成分分析(Kernel PCA)
・カーネル正準相関分析(Kernel CCA) ←気が向いたら追記します。
(なんでサポートベクタマシンやらないの?って思った方も多いかもしれませんが、ゼミがそこまでいかなかっただけです。時間があれば自分で読んでみようかなぁとは思ってます。)
カーネル法の概要
例として主成分分析を扱います。$m$次元のN個のデータ$X_1,...,X_N \in \chi=\mathbb{R}^m$に対し、単位ベクトル$u$を持ちいて射影した先$u^\mathsf{T}X$の分散がp番目に大きくなるような$u$を探します。これを第p主成分と呼び、$m$よりも少ない軸を取ることで次元圧縮やノイズ除去ができます。これを数式に書くと
\frac{1}{N}\sum_{i=1}^{N}\left\{u^{\mathsf{T}}X_{i}-\frac{1}{N}\left(\sum_{j=1}^{N}u^{\mathsf{T}}X_{j}\right)\right\}^{2}
がp番目に大きくなるように$\|u\|=1$を満たすように動かすことになります。しかし、これでは線形的な計算しか行っていないので非線形な特徴抽出はできません。そこで非線形関数でデータ$X_i$を別の空間に送ることで非線形的な計算を行います。
上記の計算で核となるのは$u$と$X$の内積です。上記の例では$\mathbb{R}^m$上で考えていたので通常の内積$\langle u,X \rangle_{\mathbb{R}^m}=u^\mathsf{T}X$が定まっています。これはデータ$X_i$を非線形写像$\phi:\chi→H$で別の空間$H$に送ったとしても、その空間に内積が定まっていれば計算できるはずです。この場合は$u$と$X$の内積$\langle u,X \rangle_{\mathbb{R}^m}$を$f \in H$を$u$の代わりに用いて$\langle f,\phi(X) \rangle_H$として主成分分析を行えばいいということです。
つまり、線形演算のみで考えていた問題を写像$\phi$を用いて別の空間に飛ばし、その空間で元の問題を考えるのがカーネル法です。従来の手法では冪展開$(X,Y,Z ... )\rightarrow(X^2, Y^2, Z^2, XY...)$を用いて非線形演算を行うのが主流でしたが、時代の変化とともに扱うデータの次元が増え、計算量が膨大になってしまう問題がありました。カーネル法では特徴写像$\phi$で送られた空間の内積を効率よく計算するカーネル関数を利用することで、通常の問題と大差ない計算量で非線形演算を可能にしています。
以上より特徴写像$\phi$と空間$H$をうまく定めるのが現在の目標です。
正定値カーネル
データ空間を$\chi$として、特徴写像$\phi$を$\phi:\chi→H$と定義します。ここで$H$は内積$\langle・,・\rangle_H$をもつ内積空間です。
その内積はある関数$k(x,y)=\langle\phi(x),\phi(y)\rangle_H$で簡単に計算できると嬉しいはずです。こうすることで、(後述する具体例で扱いますが、)$\phi$と$H$の直接的な表現を考えることなく$k$のみの表示で表せ、さらに計算コストは$\phi$に依らないことがわかります。
ここでは正定値カーネルというものを定義し、それが満たす性質を考えます。
Def 正定値カーネル
関数$k:\chi×\chi→\mathbb{R}$が以下の2つの性質を満たすとき、$k$を$\chi$上の正定値カーネルとよぶ。
・対称性:任意の$x,y \in \chi$に対し、$k(x,y)= k(y,x)$
・正定値性:任意の$n \in \mathbb{N}, x_1...x_N \in \chi, c_1...c_N \in \mathbb{R}$に対し、$\sum_{i,j=1}^{n}c_ic_jk(x_i,x_j)\geq0$
正定値性は対称性を仮定したうえで、$ij$成分が$k(x_i, x_j)$であるような$N×N$の正方行列の半正定値の定義と一致します。ここで正定値性と書いているのは、慣例から上記の定義を正定値性と呼んでいるからです。
Prop2.1
正定値カーネルに関して以下の性質が成り立ちます。
(1)$k(x,x)\geq0 \quad(\forall x \in \chi)$
(2)$|k(x,y)| \leq k(x,x)k(y,y) \quad(\forall x,y \in \chi)$
(3)$\chiの部分集合\Upsilonに対して、kの\Upsilon×\Upsilonの制限は\Upsilon上の正定値カーネルとなる。$
proof(2)
A = \left(\begin{matrix}
k(x,x) & k(x,y)\\k(x,y) & k(y,y) \end{matrix}
\right)
は半正定値対称行列で、固有値はすべて実数であり非負なので、対角化して行列式を考えると$det(A) \geq0$。また定義の通り行列式を計算しそれが非負である不等式を変形すればよい。
Prop2.2
正定値カーネルは以下の操作について閉じています。
$k_i$を正定値カーネルとします、
(1)$a,b \in \mathbb{R_{\geq0}}$に対して$ak_i+bk_j$
(2)$k_ik_j$
(3)$\lim_{n \to \infty}k_n$
proof:(2)
$k_ik_j$が成分の$N×N$行列が半正定値であればよいので、$k_i,k_j$を成分とする2つの行列のアダマール積を考え、片方の行列を対角化して正定値性の定義式に代入する。
Prop2.6
$Vを内積\langle・,・\rangle_V$を持つ内積空間とする。写像$\phi:\chi\rightarrow V , x\mapsto\phi(x)$が与えられたとき、$k(x,y)=\langle\phi(x),\phi(y)\rangle_V$は正定値カーネルとなる。
proof
正定値カーネルの定義に従い計算すればよい。
特徴写像$\phi$はこのような性質を満たすようなものが望ましかったのでした。適当に$V$を定め写像を用意すれば正定値カーネル$k$によって簡単に計算できるはずです。しかし、実は$k$を定めると$V$は一意に定まり、前述したとおり$\phi$の直接的な表現は実際の計算では必要ないことから、正定値カーネル$k$を定めればよいことがわかります。
再生核ヒルベルト空間
ここでは正定値カーネル$k$とある性質を持った内積空間$H$が一対一に対応することを確認します。
Def 再生核ヒルベルト空間
内積空間$H$を完備化したものをヒルベルト空間と言います。$\chi$を集合として、$\chi$上の関数からなるヒルベルト空間$H$で以下の性質を満たすものを再生核ヒルベルト空間と呼ぶ。
・再生性:$\forall x \in \chi, \forall f \in H, \exists k_x \in H s.t. \langle f,k_x\rangle_H = f(x)$
上の定義の$k_x \in H$に対して、$k(y,x) = k_x(y)$により定まるカーネル$k$を$H$の再生核と呼ぶ。
prop2.7
$\chi$上の再生核ヒルベルト空間$H$の再生核$k$は$\chi$上の正定値カーネルであり、$H$の再生核は一意。
proof
$k(x,y)=k_y(x)=\langle k_y, k_x\rangle_H = \langle k(・,y), k(・,x)\rangle_H$と変形できるので
$\sum_{i,j=1}^{n}c_ic_jk(x_i,x_j)\geq0$がわかる。
一意性は$k, \overline{k}$を$H$上の再生核としてそれぞれが再生核であることと対称性を用いると$k=\overline{k}$が示せる。
prop2.8
$||k(・,x)||_H=\sqrt{k(x,x)} $
proof
左辺の2乗を再生性を用いて計算すればよい。
prop2.11
集合$\chi$上の正定値カーネル$k$に対し、以下の3つの性質を満たす$\chi$上の再生核ヒルベルト空間が一意に存在する。
(1)$\forall x \in \chi, k(・,x) \in H$
(2)$k(・,x)(x \in \chi)$によって張られる部分空間(線形包)は$H$内で稠密
(3)$k$は$H$の再生核
prop2.7とprop2.11を合わせると、正定値カーネルと再生核ヒルベルト空間が1対1に対応していることがわかる。
ここで特徴写像$\phi:\chi→H$を$x \mapsto k(・,x)$と定義すると、再生性を用いれば
\begin{align}
&\begin{split}
\langle\phi(x),\phi(y)\rangle_H &= \langle k(・,x), k(・,y)\rangle_H \\
&= \langle k_x, k_y \rangle_H \\
&= k_x(y) \\
&= k(y,x) \\
&= k(x,y)
\end{split}\\
\end{align}
となるので、計算したかった内積が正定値カーネル$k$で計算できることがわかりました。
ここで、正定値カーネルのよく使われる例をいくつか紹介します。
・線形カーネル(通常のユークリッド内積)
k_0(x,y) = x^\mathsf{T} y
・指数型
k_E(x,y)=exp(\beta x^\mathsf{T} y) \ (\beta>0)
・ガウスカーネル
k_G(x,y) =exp \left(-\frac{\|x-y\|^2}{2 \sigma^2} \right)
カーネル主成分分析
簡単に理論の紹介を終えたので応用例です。
通常の主成分分析は、$u$によって射影されたときの分散を大きくなるような$||u||=1$を求めるというものでした。
\frac{1}{N}\sum_{i=1}^{N}\left\{u^{\mathsf{T}}X_{i}-\frac{1}{N}\left(\sum_{j=1}^{N}u^{\mathsf{T}}X_{j}\right)\right\}^{2}
カーネル主成分分析では特徴写像$\phi:\chi→H$を用いてデータ$X_i$を$H$上に飛ばし、$H$で内積$\langle・,・\rangle_H$を使って計算すれば非線形な特徴を捉えることができます。つまり以下の式を最大化する$f (||f||_H=1)$を求めることになります。
\frac{1}{N}\sum_{i=1}^{N}\left\{\langle f,\phi\left(X_{i}\right)\rangle_{H}\ -\ \frac{1}{N}\left(\sum_{j=1}^{N}\left\langle f,\ \phi\left(X_{j}\right)\right\rangle_H \right)\right\}^{2}
$\tilde{\phi}(X_i)=\phi(X_i) - \frac{1}{N}\sum_{i=j}^{N}\phi(X_j)$と中心化すれば、
\frac{1}{N}\sum_{i=1}^{N}\left(\langle f,\ \tilde{\phi}\left(X_{i}\right)\rangle_{H} \right)^{2}
を最大化するような$f$を考えればよいことがわかる。
$ ||f||_{H}=1$であるから、$f$は $\tilde{\phi} \left(X_{1}\right)...\tilde{\phi} \left(X_{N}\right)$で貼られる$H$の部分空間
Span\left\{\tilde{\phi}\left(X_{1}\right),...,\tilde{\phi}\left(X_{N}\right)\right\} \subset H
の要素として考えてよい。したがって、
f = \sum_{i=1}^{N}\alpha_{i}\tilde{\phi}\left(X_{i}\right)
と表せる。
つまり、さきほどの内積$\langle f, \tilde{\phi}(X_{i}) \rangle_H$は$\langle \tilde{\phi}(X_i), \tilde{\phi}(X_j) \rangle$の線形結合で表せ、$\tilde{\phi}$の中心化をとけば、$k(X_i,X_j)=\langle \phi(X_i), \phi(X_j) \rangle$であるから$k$の線形結合で表せ、係数も$\alpha$を使って表せる。したがって$\alpha$を求めることで$f$は$H$上の関数として定まり、最大化を達成できる。
ここでは簡単のために
\tilde{k}(X_i,X_j)= \langle \tilde{\phi}(X_i), \tilde{\phi}(X_j) \rangle_H
と置き、$\tilde{k}(X_i,X_j)$を$ij$成分に持つ行列を$\tilde{K}$とする。これは中心化グラム行列と呼ばれる。
最大化するする問題は以下のように変形でき、一般化固有値問題に帰着できる。
\begin{align}
&\begin{split}
\frac{1}{N}\sum_{i=1}^{N}\left(\langle f,\ \tilde{\phi}\left(X_{i}\right)\rangle_{H} \right)^{2}
&= \frac{1}{N}\sum_{i=1}^{N}\left\{\sum_{j=1}^{N}\alpha_j\tilde{k}(X_j,X_i)\right\}^{2}\\
&=\frac{1}{N}\sum_{i=1}^{N}\left\{\sum_{j=1}^{N}\sum_{k=1}^{N}\alpha_{j}\alpha_{k}\tilde{k}(X_j,X_i)\tilde{k}(X_k,X_i)\right\} \\
&= \frac{1}{N}\sum_{j=1}^{N}\sum_{k=1}^{N}\left\{\alpha_{j}\alpha_{k}\sum_{i=1}^{N}\tilde{k}(X_j,X_i)\tilde{k}(X_i,X_k)\right\}\\
&= \frac{1}{N}\sum_{j=1}^{N}\sum_{k=1}^{N}\left(\alpha_{j}\alpha_{k}\tilde{K}_{jk}^2\right)\\
&=\frac{1}{N}\alpha^\mathsf{T} \tilde{K}^2 \alpha\\
\end{split}\\
&\begin{split}
||f||_H &= \langle f, f \rangle \\
&= \langle \sum_{i=1}^{N}\alpha_{i}\tilde{\phi}\left(X_{i}\right), \sum_{j=1}^{N}\alpha_{j}\tilde{\phi}\left(X_{j}\right) \rangle \\
&= \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j \langle \tilde{\phi}(X_i), \tilde{\phi}(X_j) \rangle \\
&= \alpha^\mathsf{T} \tilde{K} \alpha
\end{split}\\
\end{align}
以上より最大化問題は
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\argmax_{\alpha \in \mathbb{R}^N} \, \alpha^\mathsf{T} \tilde{K}^2 \alpha \ \ s.t. \ \alpha^\mathsf{T} \tilde{K} \alpha = 1
$\tilde{K}$は半正定値対称行列であるから、固有値分解(対角化)すると、縦ベクトル$u^i$を$N$本並べたユニタリ行列$U$と対角行列$\Lambda=diag(\lambda_1,...,\lambda_N) \ (\lambda_1 \geq \lambda_2 \geq ...\geq \lambda_N \geq 0)$を用いて、
\tilde{K} = U \Lambda U^{*}
と分解できる。$\tilde{K}^2 = U \Lambda^2 U^{*}$であるから、
\alpha^\mathsf{T} \tilde{K}^2 \alpha = \sum_{i=1}^{N} (\alpha^\mathsf{T} u^i)^2 \lambda_i^2
したがって、$\lambda_1 \geq \lambda_2 \geq ...\geq \lambda_N \geq 0$を考えれば、p番目に大きくなる$\alpha$は$\alpha \parallel u^p$の時であり、長さは$\alpha^\mathsf{T} \tilde{K} \alpha=1$を満たすように調整すればよい。$\alpha = c_p u^p$と置けば、$u^i$はユニタリ行列の列ベクトルということに気を付けると、
\begin{align}
&\begin{split}
\alpha^\mathsf{T} \tilde{K} \alpha &= \sum_{i=1}^{N} (c_p u^{p^{\mathsf{T}}} u^i)^2 \lambda_i \\
&= c_p^2 \lambda_p
\end{split}\\
\end{align}
であるから、$c_p = \frac{1}{\sqrt{\lambda_p}}$である。
したがって分散をp番目に大きくする$f$(第p主軸)は
f^p = \sum_{i=1}^{N}\frac{1}{\sqrt{\lambda_p}} u_i^p \tilde{\phi}(X_i)
となり、データ$X_i$の第p主成分は
\begin{align}
&\begin{split}
\langle \tilde{\phi}(X_i), f^p \rangle_H &= \sum_{j=1}^N \frac{1}{\sqrt{\lambda_p}} u_j^p \langle \tilde{\phi}(X_i), \tilde{\phi}(X_j) \rangle_H \\
&= \sum_{j=1}^N \frac{1}{\sqrt{\lambda_p}} u_j^p \tilde{K}_{ij} \\
&= \sum_{j=1}^N \frac{1}{\sqrt{\lambda_p}} u_j^p \sum_{k=1}^N \lambda_k u_i^k u_j^k \\
&= \frac{1}{\sqrt{\lambda_p}} \sum_{k=1}^N \lambda_k u_i^k \sum_{j=1}^N u_j^p u_j^k \\
&= \frac{1}{\sqrt{\lambda_p}} \sum_{k=1}^N \lambda_k u_i^k \delta(p,k) \\
&= \sqrt{\lambda_p} u_i^p
\end{split}\\
\end{align}
つまり、$\tilde{k}(X_i,X_j)$を$ij$成分に持つ行列$\tilde{K}$を固有値分解したときの固有値とユニタリ行列がわかれば十分である。
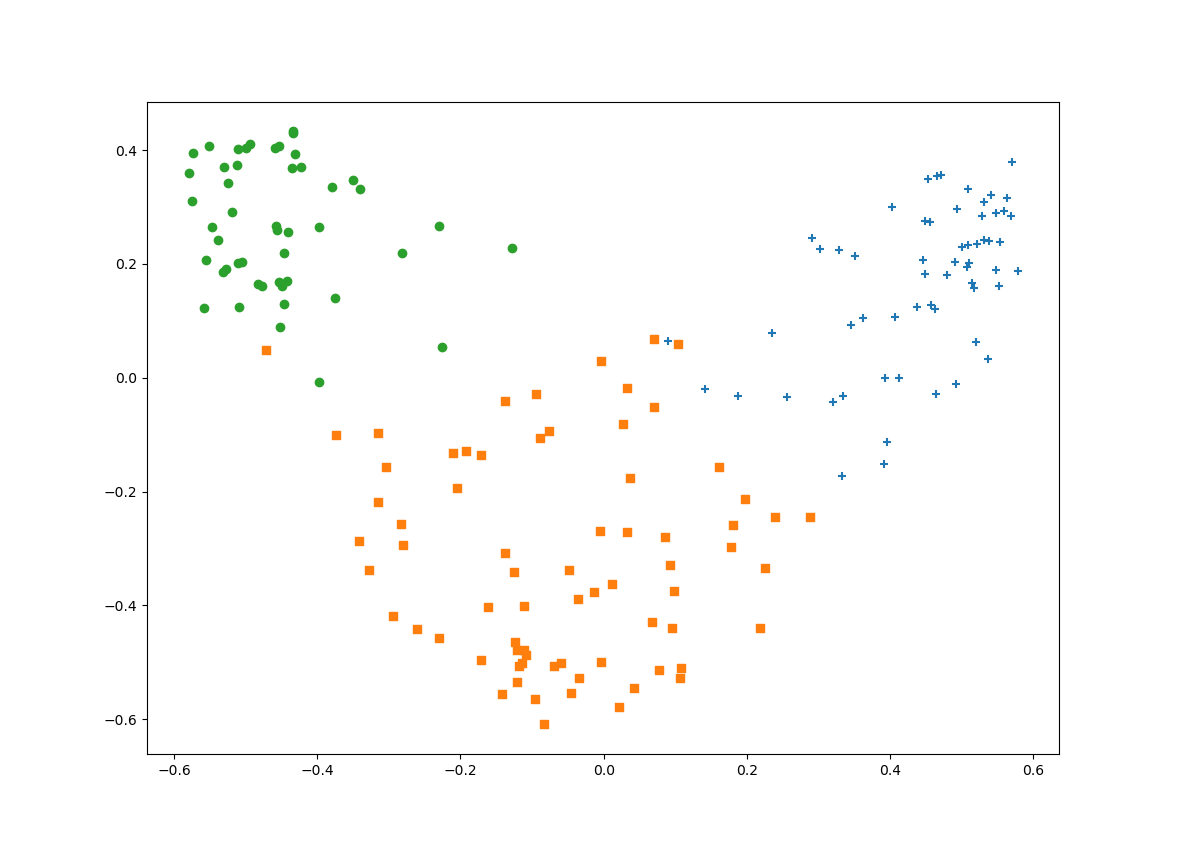
以上をPythonを用いて実装する。データにはワインデータ(http://archive.ics.uci.edu/ml/datasets/Wine)
を利用する。
カーネル関数にはガウスカーネルを使うことにする。
import numpy as np
import matplotlib.pyplot as plt
# データの読み込み
wine = np.loadtxt("wine.csv", delimiter=",")
N = wine.shape[0] #178
labels = np.copy(wine[:,0]).flatten()
wine = wine[:, 1:]
# 標準化
mean = wine.mean(axis=0)
wine -= mean
std = wine.std(axis=0)
wine /= std
def kernel(x,y, σ=4): return np.exp(-((x-y)**2).sum() / (2*σ**2))
# 中心化グラム行列Kの計算
K = np.zeros(shape=(N,N))
for i,j in np.ndindex(N,N):
K[i,j] = kernel(wine[i,:], wine[j,:])
Q = np.identity(N) - np.full(shape=(N,N), fill_value=1/N)
K_tilde = Q @ K @ Q
# 固有値分解
λs, us = np.linalg.eig(K_tilde)
# 固有値の大きい順に並べ替え
λ_index = np.argsort(λs)
D = np.zeros(shape=(N))
U = np.zeros(shape=(N,N))
for i, index in enumerate(λ_index[::-1]):
D[i] = λs[index]
U[:,i] = us[:,index]
# データの第n主成分
X_1 = np.sqrt(D[0]) * U[:,0]
X_2 = np.sqrt(D[1]) * U[:,1]
# グラフの作成
clasters = dict([(i,[[],[]]) for i in range(1,4)])
for i,label in enumerate(labels):
clasters[label][0].append(X_1[i])
clasters[label][1].append(X_2[i])
for label,marker in zip(range(1,4), ["+","s","o"]):
plt.scatter(clasters[label][0], clasters[label][1], marker=marker)
plt.show()
いい感じに分類できていることがわかります。
ちなみにカーネル関数の選び方でグラフの形が大きく変わります。同じガウスカーネルでもハイパーパラメータの設定によって変わるので、グリッドサーチみたいなことをしてもいいですね。
参考文献
福水健次, カーネル法入門[正定値カーネルによるデータ解析], 朝倉書店, 2010年