はじめに
この記事は普段C++とかTypeScriptに慣れ親しんでいる、pythonもソルバーとか使ったことない筆者がpythonとpulpというソルバーライブラリを使ってみる記事です。
「あんたがた」シリーズ第二弾です
前作→#atgt2019 14匁にC++の力で挑んだが甜菜はそんなものをふっとばして答えにたどり着く - Qiita
atgtとは
「あめちゃん」が考案し、2ちゃんねるVIP板にて開催された「VIPPERのあんたがたに挑戦します」
その遊びはTwitterの世界に持ち込まれ、有志によって続いてきました。
その正当な流れを組みつつ、新型コロナウィルス対策を施したルールにより、
ステイホームのゴールデンウィークを最高にwktkなものにしてくれたイベント、
それが「ツイッターのあんたがたに挑戦します2020GW」です。
- このイベントは全体戦で、「ツイッターのあんたがたに挑戦します2020GW」のパロディです。
本家GMの皆様におかれましては、本当にごめんなさい。そして心から御礼申し上げます。
パロディの程度や内容については、実戦でお確かめください。 - 本家GM以外のあんたがたも積極的にご参加ください。本家ほどではありませんが、難易度も分量もかなりのレベルです。
- ハッシュタグは #atgm_2020 を使用してください。
- 本イベントに関するツイートにはこのハッシュタグを付けてください。
- GM側からあんたがたに対するサポートは、問題が長時間解けない時のヒント出しです。
ヒントを出す前に、それが必要かどうかの投票を行います。 - このイベントで外出が必要なものはありません。暑い季節ですので、あんたがた各自で水分塩分糖分を補給する、睡眠を十分に確保するなど、健康管理に注意してください。
- 一般の方々には絶対に迷惑をかけない。
- 転んでも泣かない。そして楽しむ心が大事です。
12匁
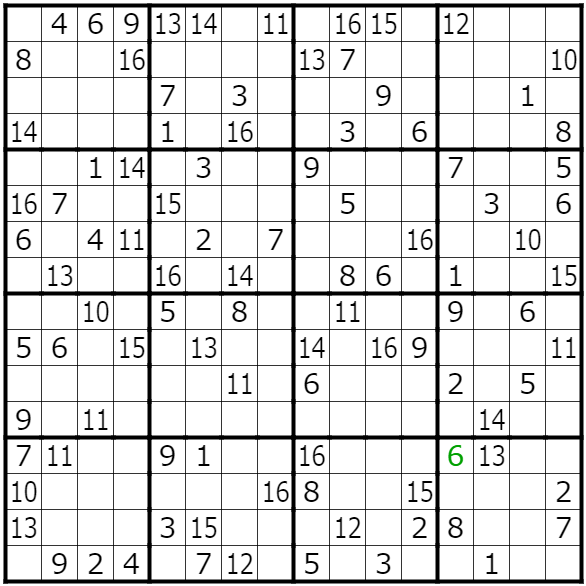
さて、そうして始まったatgm_2020の12問目、問題を解き進めていくと、16x16の巨大な変則的数独を解く必要が出てきました。
9x9の通常の数独を拡張しただけではなく、
диагональ(対角線)
対角線上も重複してはいけないというルールでした。
ひんと#atgm_2020 pic.twitter.com/BXyALwv0KR
— 2020GW運営のあんたがたに挑戦します (@atgm_2020) July 25, 2020
しかし人力で解き進めるにはいささか難しすぎるものでした
こういうのはソルバーに解かせたほうが速いのでは???
解かせ方
数独問題を制約充足問題として定義すれば、最適化の汎用ソルバーで解けますよねという方法です。この方法でも解があれば必ず見つかります。
正直ソルバーの類は扱ったことがないのですが、やってみます。
幸いこの記事には「Pulp使ったConstraint programming」のソースコードが提供されています。
残念なお知らせはpythonで書かれていることです。なぜ残念なお知らせかといえば、どういうわけか私がpythonでなにかしようとするたびに、なにかしらのエラーに遭遇して動かないからですね。まあせめてエラーに遭遇しにくいLinux環境を用意しましょう。
$ sudo apt-get install python3-distutils
$ curl https://bootstrap.pypa.io/get-pip.py -o get-pip.py
$ sudo python3 get-pip.py
$ python3 -m pip install pulp
とりあえずそこらへんに転がってたUbuntu18.04のVPSにSSHしたところ、pipすらなかったのでそこから導入しました。python3-distutilsがないとsudo python3 get-pip.pyがコケるとかまじですか・・・。
元記事のコードを理解する
内包記法
digits = [str(d + 1) for d in range(n)]
boxes = [[(rows[b * i + k], columns[b * j + l]) for k in range(b) for l in range(b)] for j in range(b) for i in range(b)]
でたな、内包記法。他の言語ではなかなかお目にかかれない頭のおかしい特徴的な記法ですね。rangeは[0...n)の整数列をつくるやつですね。
LpVariable.dicts
choices = LpVariable.dicts("Choice", (values, rows, columns), 0, 1, LpInteger)
PuLP による線型計画問題の解き方ことはじめ - Qiita
によればpulpで変数オブジェクトを作る方法の一つのようですね。
多分Choice_1_1_1, Choice_1_1_2, ...って感じの変数名が作られていくのだと思います。基本的に0が入って、埋まったら1なのかな?
目的関数
problem = LpProblem("Solving Sudoku", LpMinimize) # MinimizeでもMaximizeでもOK
problem += 0, "Arbitrary Objective Function"
目的関数が0ってどういうことなんでしょうね、任意の目的関数とか言われても、ちょっと良くわかりません。
制約
for v in values:
for r in rows:
problem += lpSum([choices[v][r][c] for c in columns]) == 1, ""
for c in columns:
problem += lpSum([choices[v][r][c] for r in rows]) == 1, ""
for b in boxes:
problem += lpSum([choices[v][r][c] for (r, c) in b]) == 1, ""
for i in range(n**2):
val = inp[i]
if val != '0':
problem += choices[str(val)][str(i/n + 1)][str(i % n + 1)] == 1, ""
LpVariable.dictsで作った変数は3次元なのでchoices[v][r][c]みたいにアクセスすると個々の変数が取れるようです。
lpSumは名前の通り合計ですね。普通のsumを使うとO(n^2)のオーダーになる、って書いてる記事があるんですが、どういう理屈なんだろうか。
上から順に
- 各ますには一つの数字しか入らない
- 各列に同じ数字は1つ
- 各行に同じ数字は1つ
- 3x3 の中に同じ数字は一つ
- もとから入ってる数字
という制約だと思います。
再制約
while True:
# cbcソルバー利用
problem.solve()
if LpStatus[problem.status] == "Optimal":
answers.append(''.join([v for r in rows for c in columns for v in values if value(choices[v][r][c]) == 1]))
# 見つけた解を制約として追加
problem += lpSum(
[choices[v][r][c] for v in values for r in rows for c in columns if value(choices[v][r][c]) == 1]
) <= 80
else:
break
何をやってるのかさっぱりです。80って何???
今回の問題に合わせて書き換える
盤面の大きさが違うのをまず直します
- n = 9
- b = 3
+ n = 16
+ b = 4
それから追加の制約が必要です。対角線のことを制約に加えましょう。rangeをサクッとzipできるのいいですね、C++も外部ライブラリじゃなくて標準でできるようになってほしい(C++20ではまだなかったはず)
problem += lpSum([choices[v][i][i] for i in range(n)]) == 1, ""
problem += lpSum([choices[v][r][c] for (r, c) in zip(range(n), reversed(range(n)))]) == 1, ""
KeyError: 0
Traceback (most recent call last):
File "solve.py", line 62, in <module>
main(f)
File "solve.py", line 35, in main
problem += lpSum([choices[v][i][i] for i in range(n)]) == 1, ""
File "solve.py", line 35, in <listcomp>
problem += lpSum([choices[v][i][i] for i in range(n)]) == 1, ""
KeyError: 0
だめじゃん。
Python - KeyError pulpを使って特殊な数独を解きたいがエラーが出る|teratail
で質問したところ次のようなことがわかりました。
digits = [str(d + 1) for d in range(n)]
values = rows = columns = digits
より、keyは'1'~'16'という文字列なのに、0~15の数値をkeyにしていることが問題だったようです。
problem += lpSum([choices[v][str(i + 1)][str(i + 1)] for i in range(n)]) == 1, ""
problem += lpSum([choices[v][str(r + 1)][str(c + 1)] for (r, c) in zip(range(n), reversed(range(n)))]) == 1, ""
というわけで制約条件を見直しました。
入力の与えかたを変更
元記事では長大な数値列をコマンドライン引数として渡していました。しかしこれは使いにくいし、そもも盤面が大きくなったことで入力を1文字ずつ取り出すわけにはいかなくなりました。
素直にcsvを使いましょう。
当初
pythonでのcsvファイルの読み込み - Qiita
を見て
f = csv.reader("input.csv", delimiter=",", doublequote=True, lineterminator="\r\n", quotechar='"', skipinitialspace=True)
でリストくれるしいいじゃんと思ってたのですが、TypeError: '_csv.reader' object is not subscriptableとか言われるらしいですね、ようはイテレータで逐次読み出すような実装だからそのものはリストじゃなくって、だから添字アクセスできません、ということだろうか。
teratailでの指摘通り
with open('input.csv') as fp:
f = []
lines = fp.read().splitlines()
for line in lines:
f += line.split(',')
にしました。
出力の変更
やっぱり数値列そのまま出てくる元記事のは読めないので整形したいなと思っていたらteratailで回答してくれた人がついでに教えてくれました。
import numpy as np
ans = np.array([int(v) for r in rows for c in columns for v in values if value(choices[v][r][c]) == 1]).reshape(16,-1)
answers.append(ans)
# answers.append(''.join([v for r in rows for c in columns for v in values if value(choices[v][r][c]) == 1]))
こんなふうに書き換えました。
最終的なプログラム
# -*- coding: utf-8 -*-
import argparse
import numpy as np
from pulp import LpVariable, LpInteger, LpProblem, LpMinimize, LpStatus, lpSum, value
def main(inp):
n = 16
b = 4
digits = [str(d + 1) for d in range(n)]
values = rows = columns = digits
answers = []
choices = LpVariable.dicts("Choice", (values, rows, columns), 0, 1, LpInteger)
boxes = [[(rows[b * i + k], columns[b * j + l]) for k in range(b) for l in range(b)] for j in range(b) for i in range(b)]
# 問題提議
problem = LpProblem("SolvingSudoku", LpMinimize) # MinimizeでもMaximizeでもOK
problem += 0, "Arbitrary Objective Function"
# 制約追加
for r in rows:
for c in columns:
problem += lpSum([choices[v][r][c] for v in values]) == 1, ""
for v in values:
for r in rows:
problem += lpSum([choices[v][r][c] for c in columns]) == 1, ""
for c in columns:
problem += lpSum([choices[v][r][c] for r in rows]) == 1, ""
for b in boxes:
problem += lpSum([choices[v][r][c] for (r, c) in b]) == 1, ""
problem += lpSum([choices[v][str(i + 1)][str(i + 1)] for i in range(n)]) == 1, ""
problem += lpSum([choices[v][str(r + 1)][str(c + 1)] for (r, c) in zip(range(n), reversed(range(n)))]) == 1, ""
for i in range(n**2):
val = inp[i]
if val != '0':
problem += choices[str(val)][str(i // n + 1)][str(i % n + 1)] == 1, ""
while True:
# cbcソルバー利用
problem.solve()
if LpStatus[problem.status] == "Optimal":
ans = np.array([int(v) for r in rows for c in columns for v in values if value(choices[v][r][c]) == 1]).reshape(16,-1)
answers.append(ans)
# answers.append(''.join([v for r in rows for c in columns for v in values if value(choices[v][r][c]) == 1]))
# 見つけた解を制約として追加
problem += lpSum(
[choices[v][r][c] for v in values for r in rows for c in columns if value(choices[v][r][c]) == 1]
) <= 80
else:
break
if answers:
# 最初の解だけ表示
print(answers[0])
if __name__ == '__main__':
with open('input.csv') as fp:
f = []
lines = fp.read().splitlines()
for line in lines:
f += line.split(',')
main(f)
0,4,6,9,13,14,0,11,0,16,15,8,12,0,0,3
8,0,0,16,0,0,0,0,13,7,0,0,0,0,0,10
11,0,0,0,7,0,3,0,0,0,9,0,0,0,1,0
14,0,0,0,1,0,16,0,0,3,0,6,0,0,0,8
0,0,1,14,0,3,0,0,9,0,0,0,7,0,0,5
16,7,0,0,15,0,0,0,0,5,0,0,0,3,0,6
6,0,4,11,0,2,0,7,0,0,0,16,0,0,10,9
0,13,0,0,16,0,14,0,0,8,6,0,1,0,0,15
0,0,10,0,5,0,8,0,0,11,0,0,9,0,6,0
5,6,0,15,0,13,0,0,14,0,16,9,0,0,0,11
0,0,0,0,0,0,11,0,6,0,0,0,2,0,5,0
9,0,11,0,0,0,0,0,0,0,0,0,0,14,0,0
7,11,0,8,9,1,0,0,16,0,0,0,0,13,0,0
10,0,0,0,0,0,13,16,8,9,7,15,0,0,0,2
13,0,0,0,3,15,0,0,0,12,0,2,8,0,0,7
15,9,2,4,0,7,12,0,5,0,3,0,0,1,0,0
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
command line - /home/yumetodo/.local/lib/python3.6/site-packages/pulp/apis/../solverdir/cbc/linux/64/cbc /tmp/86dc532bb7f1470791450da595738a61-pulp.mps branch printingOptions all solution /tmp/86dc532bb7f1470791450da595738a61-pulp.sol (default strategy 1)
At line 2 NAME MODEL
At line 3 ROWS
At line 1167 COLUMNS
At line 26363 RHS
At line 27526 BOUNDS
At line 31624 ENDATA
Problem MODEL has 1162 rows, 4097 columns and 17002 elements
Coin0008I MODEL read with 0 errors
Continuous objective value is 0 - 0.00 seconds
Cgl0003I 24 fixed, 0 tightened bounds, 0 strengthened rows, 0 substitutions
Cgl0003I 361 fixed, 0 tightened bounds, 0 strengthened rows, 124 substitutions
Cgl0003I 111 fixed, 0 tightened bounds, 0 strengthened rows, 8 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 0 strengthened rows, 8 substitutions
Cgl0004I processed model has 0 rows, 0 columns (0 integer (0 of which binary)) and 0 elements
Cbc3007W No integer variables - nothing to do
Cuts at root node changed objective from 0 to -1.79769e+308
Probing was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Gomory was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Knapsack was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Clique was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
MixedIntegerRounding2 was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
FlowCover was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
TwoMirCuts was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Result - Optimal solution found
Objective value: 0.00000000
Enumerated nodes: 0
Total iterations: 0
Time (CPU seconds): 0.50
Time (Wallclock seconds): 0.54
Option for printingOptions changed from normal to all
Total time (CPU seconds): 0.53 (Wallclock seconds): 0.58
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
command line - /home/yumetodo/.local/lib/python3.6/site-packages/pulp/apis/../solverdir/cbc/linux/64/cbc /tmp/31c316a84f9740ac877548623e61cbc7-pulp.mps branch printingOptions all solution /tmp/31c316a84f9740ac877548623e61cbc7-pulp.sol (default strategy 1)
At line 2 NAME MODEL
At line 3 ROWS
At line 1168 COLUMNS
At line 26620 RHS
At line 27784 BOUNDS
At line 31882 ENDATA
Problem MODEL has 1163 rows, 4097 columns and 17258 elements
Coin0008I MODEL read with 0 errors
Problem is infeasible - 1.54 seconds
Option for printingOptions changed from normal to all
Total time (CPU seconds): 1.57 (Wallclock seconds): 1.64
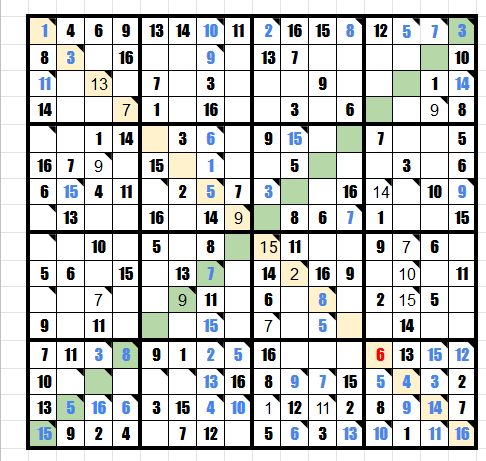
[[ 1 4 6 9 13 14 10 11 2 16 15 8 12 5 7 3]
[ 8 3 5 16 2 12 9 15 13 7 14 1 11 6 4 10]
[11 2 13 12 7 8 3 6 4 10 9 5 15 16 1 14]
[14 10 15 7 1 5 16 4 11 3 12 6 13 2 9 8]
[ 2 8 1 14 10 3 6 13 9 15 4 11 7 12 16 5]
[16 7 9 10 15 11 1 8 12 5 2 14 4 3 13 6]
[ 6 15 4 11 12 2 5 7 3 1 13 16 14 8 10 9]
[ 3 13 12 5 16 4 14 9 10 8 6 7 1 11 2 15]
[ 4 14 10 2 5 16 8 12 15 11 1 3 9 7 6 13]
[ 5 6 8 15 4 13 7 1 14 2 16 9 3 10 12 11]
[12 16 7 13 14 9 11 3 6 4 8 10 2 15 5 1]
[ 9 1 11 3 6 10 15 2 7 13 5 12 16 14 8 4]
[ 7 11 3 8 9 1 2 5 16 14 10 4 6 13 15 12]
[10 12 14 1 11 6 13 16 8 9 7 15 5 4 3 2]
[13 5 16 6 3 15 4 10 1 12 11 2 8 9 14 7]
[15 9 2 4 8 7 12 14 5 6 3 13 10 1 11 16]]
というわけで結果が求められました。
余談
私がpythonと格闘している最中に別の人がやっぱりソルバー使ってすでに答えを求めてました。
#atgm_2020
— 古銅@マイクラリソパ民 (@txkodo) July 25, 2020
未検証だがおそらく解答 pic.twitter.com/F5Zj7UPE7d