はじめに

C++erの皆様へ

本当は三項演算子(条件演算子)について、規格書を丹念に読み進めていく記事にするはずでした。

C++の三項演算子の仕様は要するに「2つの式から共通の型を導出するのをなるべく頑張る」で、それはstd::common_(type|reference)の仕様にダイレクトにつながって、そこからさらに複数のrangeを1つのrangeに見せるアダプタ等にも綺麗につながる発展性のある話になる予定（私的に）なので誰か頑張れ。
— Akso de la Malbono (@Cryolite) November 6, 2019

それ、必要なのはstd::common_typeの解説であって三項演算子関係ないやん

そしてそれには規格書でも丸々一章くらい割いてる型変換周りの仕様を全部解説しないといけない。 https://t.co/KB2Mq5EiLK
— yumetodo-鳥の氷河から逃げる (@yumetodo) November 7, 2019

std::common_type の解説に三項演算子関係無いですか？
— Akso de la Malbono (@Cryolite) November 7, 2019

std::common_type の仕様は記述の大幅な簡略化のために decltype(false ? declval<X(&)()>()() : declval<Y(&)()>()()) や decay_t<decltype(false ? declval<D1>() : declval<D2>())> を refer すると言う離れ業をしているわけで，ここがポイントになりませんか？
— Akso de la Malbono (@Cryolite) November 7, 2019

これらがきっかけです。

しかしながら、執筆現在(2019/12/24)全く調べておらず、また規格書を一章まるごと翻訳するに近い作業が発生することから、今年のAdvent Carenderの記事にするのは断念しました。

そこでatgt(後述)というイベントでC++のコードを書いたのでそれの解説でもしながらお茶を濁します。

例年真面目な記事?を書いてきたのに期待されていた方(いないって)、ごめんなさい。

atgtから来た方へ

どうも、4匁で勇者として藤野に凸してきたのは私です。

その記録をまだお読みでない方は

atgt2019 4匁勇者記録 - yumetodoの旅とプログラミングとかの記録

をお読みください。あとついでに

#atgt2019 10匁　青信号はそのまま通過ルール検証

もよかったら見てやってください。マイクラ検証班で録画担当してました。

atgtとは

「あめちゃん」が考案し、平成17年2月に2ちゃんねるVIP板にて開催された「VIPPERのあんたがたに挑戦します」。

GMが提示したパスワードから出題される謎を解き、その答えが指し示す場所に突撃すると、そこには次のパスワードが。

全国に散らばった謎を辿り、顔も知らない仲間達と協力する、世界で最もｗｋｔｋな遊びです。

そして、その遊びはTwitterの世界にも持ち込まれました。それが「Twitterのあんたがたに挑戦します」です。

ルール

8桁のパスワードをメモし、財布を持ってセブンイレブンへ。
コピー機で「ネットプリント」を選択し、パスワードを入力して問題を印刷。
印刷された問題を解いて現地を突き止める。
現地でパスワードが書かれたガムテープを探す。
1～4を繰り返し、ゴールを目指す。

atgtでの慣習とか用語(記事を読むに当たり必要そうなもの抜粋)

問題がリレーして出てくるわけですが、順番に普通なら1問目、2問目・・・と書くところを、atgtでは「匁」を使って表す傾向にあります。 ex.) 14問目→14匁
天才→甜菜
問題を回答する道筋が立たずに行き詰まっているときに、pspsと表現する
ガムテープがある現地に行く人を勇者と呼ぶ
勇者が見つけたガムテープに書かれたネットプリントのパスワードを使ってセブンイレブンに印刷しに行って上げる人を「せばん」と呼ぶ(ただし「あ」は1以上の任意個数、セバアアアンなど)
Google Spread sheetで共同作業して模索することが近年しばしば行われる。これにかじりつく担当をスプシ担当と呼ぶ(嵐防止のためにリンクはしません、全貌が一発でわかるので検索して見てきてください)

14匁

問題

どうやってここまでたどり着いたかはTwitterで各自#atgt2019を検索してほしいが、とにかく13匁を解いて現地(つくばセンタービル　緑色の自動販売機)に行ったところ、セブンイレブンのネットプリントのパスワード(89159986、ネットプリントの有効期限には注意)を入手した

つくばです！！！せばんさんおねがいしまあああああす #atgt2019 pic.twitter.com/9XSzM2N8VW
— ーちっぃ@謎@ぃっちー (@_icchicchi0903_) December 23, 2019

セブンイレブンのネットプリントを使ったことがある人ならご存知と思うが、ネットプリントするときにファイル名を見ることができる。ファイル名も問題を解く手がかりとなる。ファイル名は「白か黒か」だった。

白か黒か #atgt2019 pic.twitter.com/tF6LBK7J2f
— りー🦁🦁 (@leafed_riaf) December 23, 2019

この記事を書くためだけに、自分もさっき近くのセブンイレブンに行って印刷してきたのがこちらだ。

ここからガムテープがある場所と現地でガムテープを探すときのヒントを特定する。

ガムテープは大抵は日本国内のどこかにある。たまにシカゴとか釜山とかベトナム(←NEW)とかいう海外にあったりするが。

試行錯誤

一筋縄では行かない問題で様々な模索が行われた。オセロとか、問題文下が途切れてることからループ説が出てオルゴールとか、音ゲーの譜面じゃないかとか、幅が16ますなので文字コード表のどこかじゃないかとか、数字をアルファベットに置き換えてみたり、数字を順番に線で結んでなんか図形が見えないか調べたりなどなど・・・。

一つの道筋

そんななか、私が目にしたツイートがこれだ。

#atgt2019
Excelみたいに
1から2まで範囲指定して白黒反転
2から3まで範囲指定して白黒反転
繰り返したら何か浮かび上がるとか？
— こーた (@escape1008) December 23, 2019

面白いので検証しようとしたが、これを人力でやるには面倒すぎる。2から3までやった時点であきた。

そういうわけでプログラムの出番やろ！

検証するプログラムを書く

というわけで私の得意言語、C++の出番だ。

せっかくなのでsproutのちからを借りてコンパイル時に結果を求めよう。(というのもstd::bitsetはconstexprに操作できない)

コード

#include <iostream>    
#include <string>
#include <sprout/bitset.hpp>
#include <array>
#include <algorithm>
template<std::size_t N>
constexpr sprout::bitset<N> reverse(const sprout::bitset<N> &bit_set) {
    sprout::bitset<N> reversed;
    for (std::size_t i = 0, j = N - 1; i < N; i++, j--) {
        reversed[j] = bit_set[i];
    }
    return reversed;
}
//y:20 x:16
class table {
public:
    inline static constexpr std::size_t width = 16;
    inline static constexpr std::size_t height = 20;
    using line_t = sprout::bitset<width>;
    using number_table_t = std::array<std::array<std::uint8_t, width>, height>;
    using pos_t = std::pair<std::uint8_t, std::uint8_t>;
    using color_table_t = std::array<line_t, height>;
private:
    inline static constexpr color_table_t t_base = {
        reverse<width>(0b0001100000011000),
        reverse<width>(0b1000000001011111),
        reverse<width>(0b0001101000011010),
        reverse<width>(0b1001001001011111),
        reverse<width>(0b0000100000000000),
        reverse<width>(0b0000001000001111),
        reverse<width>(0b0100000100000001),
        reverse<width>(0b0010001000001111),
        reverse<width>(0b0000100011011101),
        reverse<width>(0b0100111111111000),
        reverse<width>(0b0100100011010101),
        reverse<width>(0b0100111111111000),
        reverse<width>(0b0100110000011000),
        reverse<width>(0b0101000000011000),
        reverse<width>(0b0010100000001000),
        reverse<width>(0b0100000000001000),
        reverse<width>(0b0000000000011101),
        reverse<width>(0b0000010000011101),
        reverse<width>(0b0100010000001000),
        reverse<width>(0b0001000000000000)
    };
    color_table_t t = t_base;
    inline static constexpr std::array<pos_t, 36> pos{{
        /* 0-startで数字のxy座標 */
        /* 1*/{  5u, 10u },
        /* 2*/{  4u,  3u },
        /* 3*/{ 10u, 16u },
        /* 4*/{  0u, 18u },
        /* 5*/{ 12u,  6u },
        /* 6*/{  0u,  7u },
        /* 7*/{  8u,  6u },
        /* 8*/{  4u, 13u },
        /* 9*/{ 15u, 15u },
        /*10*/{ 10u,  6u },
        /*11*/{  8u, 13u },
        /*12*/{  6u, 15u },
        /*13*/{  1u,  5u },
        /*14*/{  0u,  9u },
        /*15*/{  9u, 19u },
        /*16*/{ 13u, 18u },
        /*17*/{  9u,  0u },
        /*18*/{  0u, 16u },
        /*19*/{ 14u, 11u },
        /*20*/{  6u, 18u },
        /*21*/{  9u,  2u },
        /*22*/{  0u, 12u },
        /*23*/{  9u, 17u },
        /*24*/{ 13u,  2u },
        /*25*/{ 15u,  2u },
        /*26*/{ 15u,  0u },
        /*27*/{  1u,  1u },
        /*28*/{  2u,  1u },
        /*29*/{  3u,  1u },
        /*30*/{  4u,  1u },
        /*31*/{  5u,  1u },
        /*32*/{  6u,  1u },
        /*33*/{  7u,  1u },
        /*34*/{  8u,  1u },
        /*35*/{ 10u,  1u }
    }};
    inline constexpr void fill(pos_t p1, pos_t p2)
    {
        const auto [x1, x2] = std::minmax(p1.first, p2.first);
        const auto [y1, y2] = std::minmax(p1.second, p2.second);
        line_t mask{};
        for(auto i = x1; i <= x2; ++i) mask.set(i);
        for(auto i = y1; i <= y2; ++i) this->t[i] ^= mask;
    }
public:
    inline static constexpr number_table_t create_base_table()
    {
        number_table_t re{};
        for(std::size_t i{}; i < pos.size(); ++i) {
            const auto [x, y] = pos[i];
            re[y][x] = i + 1u;
        }
        return re;
    }
    table() = default;
    inline constexpr color_table_t fill_all()
    {
        for(std::size_t i = 1u; i < pos.size(); ++i) {
            this->fill(pos[i - 1u], pos[i]);
        }
        return this->t;
    }
};
constexpr table::number_table_t base_table = table::create_base_table();
inline constexpr auto calc()
{
    table t{};
    return t.fill_all();
}
int main()
{
    constexpr auto re = calc();
    for(auto l : re) {
        for(std::size_t i{}; i < l.size(); ++i) {
            if (i) std::cout << ',';
            std::cout << l[i];
        }
        std::cout << std::endl;
    }
    std::cout << std::endl;
    for(auto&& l : base_table) {
        bool first = true;
        for(auto&& e : l) {
            if (!std::exchange(first, false)) std::cout << ',';
            std::cout << int(e);
        }
        std::cout << std::endl;
    }
}

解説

色の反転ということは黒と白の2値しかないのだから、これはboolの出番だ。

ここでは黒をtrue(=1),白をfalse(=0)とする。

また、数値が含まれている範囲だけが対象だから

のように座標を取ることにした。

`std::bitset`

C++には２進数数値リテラルがあるので表の一列はstd::bitsetを使って

#include <iostream>    
#include <string>
#include <bitset>
int main()
{
    std::bitset<16> b{0b1000100001011111};
    for(std::size_t i{}; i < b.size(); ++i) {
        std::cout << b[i] << ',';
    }
}

のように書ける・・・ということはない。

出力例

1,1,1,1,1,0,1,0,0,0,0,1,0,0,0,1,

バイトオーダーとかに依存して意図したようにならない。

さしあたってどうせコンパイル時に実行するので単純にforを回してひっくり返す関数をStackOverflowで探してきた

c++ - How to reverse bits in a bitset? - Stack Overflow

#include <iostream>    
#include <string>
#include <sprout/bitset.hpp>
template<std::size_t N>
constexpr sprout::bitset<N> reverse(const sprout::bitset<N> &bit_set) {
    sprout::bitset<N> reversed;
    for (std::size_t i = 0, j = N - 1; i < N; i++, j--) {
        reversed[j] = bit_set[i];
    }
    return reversed;
}
int main()
{
    constexpr auto b = reverse<16>(0b1000100001011111);
    for(std::size_t i{}; i < b.size(); ++i) {
        std::cout << b[i] << ',';
    }
}

実行例

1,0,0,0,1,0,0,0,0,1,0,1,1,1,1,1,

数値の表を作る

1～36までの数値はその(x,y)座標をstd::pairで管理した。これは後述の色の反転処理には便利だが、最終的には表の形でほしいので作る。数値が入らないところは0にする。

    inline static constexpr number_table_t create_base_table()
    {
        number_table_t re{};
        for(std::size_t i{}; i < pos.size(); ++i) {
            const auto [x, y] = pos[i];
            re[y][x] = i + 1u;
        }
        return re;
    }

色の反転

まず2点の座標がp1, p2で与えられる。std::minmaxを使って左上と右下の座標に変換する。

まず[x1, x2](閉区間)のbitを立てたmaskを作る。

そして[y1, y2]の範囲の行に対してさっきのmaskとxorを取ればいい。xorで済むというのはとってもシンプルでいい。

    inline constexpr void fill(pos_t p1, pos_t p2)
    {
        const auto [x1, x2] = std::minmax(p1.first, p2.first);
        const auto [y1, y2] = std::minmax(p1.second, p2.second);
        line_t mask{};
        for(auto i = x1; i <= x2; ++i) mask.set(i);
        for(auto i = y1; i <= y2; ++i) this->t[i] ^= mask;
    }

あとはこれを全部の数字について実行すればいい。

    inline constexpr color_table_t fill_all()
    {
        for(std::size_t i = 1u; i < pos.size(); ++i) {
            this->fill(pos[i - 1u], pos[i]);
        }
        return this->t;
    }

結果

0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,0
1,0,1,1,1,1,1,1,1,0,0,1,1,1,0,1
0,0,0,1,1,0,0,1,1,1,0,1,1,1,0,0
1,0,0,1,0,0,1,0,0,1,1,1,1,1,1,1
0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0
1,0,1,1,1,1,0,0,0,0,1,0,1,1,1,1
0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0
0,1,1,0,1,1,0,0,1,1,1,1,0,0,0,0
0,1,0,0,0,1,1,0,0,1,0,1,1,0,1,0
1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1
0,0,1,1,1,0,0,1,1,0,0,1,0,0,1,0
1,1,0,0,1,1,1,0,1,0,1,1,1,1,1,1
0,0,1,1,0,0,1,0,1,0,0,1,1,1,1,1
1,1,0,1,1,1,0,1,0,0,1,0,0,0,0,0
1,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0
1,1,0,0,0,0,1,0,0,1,0,1,0,0,0,0
0,0,0,0,1,1,1,1,1,1,1,0,0,1,0,1
0,0,0,0,0,1,0,0,0,0,1,1,1,0,1,1
1,0,1,1,1,0,1,1,1,1,1,0,1,1,1,0
1,1,1,0,1,1,1,1,1,0,1,1,1,1,0,0

36,0,0,0,0,0,0,0,0,17,0,0,0,0,0,26
0,27,28,29,30,31,32,33,34,0,35,0,0,0,0,0
0,0,0,0,0,0,0,0,0,21,0,0,0,24,0,25
0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
0,13,0,0,0,0,0,0,0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0,7,0,10,0,5,0,0,0
6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
14,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0,0,0,0,0,0,0,19,0
22,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
0,0,0,0,8,0,0,0,11,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
0,0,0,0,0,0,12,0,0,0,0,0,0,0,0,9
18,0,0,0,0,0,0,0,0,0,3,0,0,0,0,0
0,0,0,0,0,0,0,0,0,23,0,0,0,0,0,0
4,0,0,0,0,0,20,0,0,0,0,0,0,16,0,0
0,0,0,0,0,0,0,0,0,15,0,0,0,0,0,0

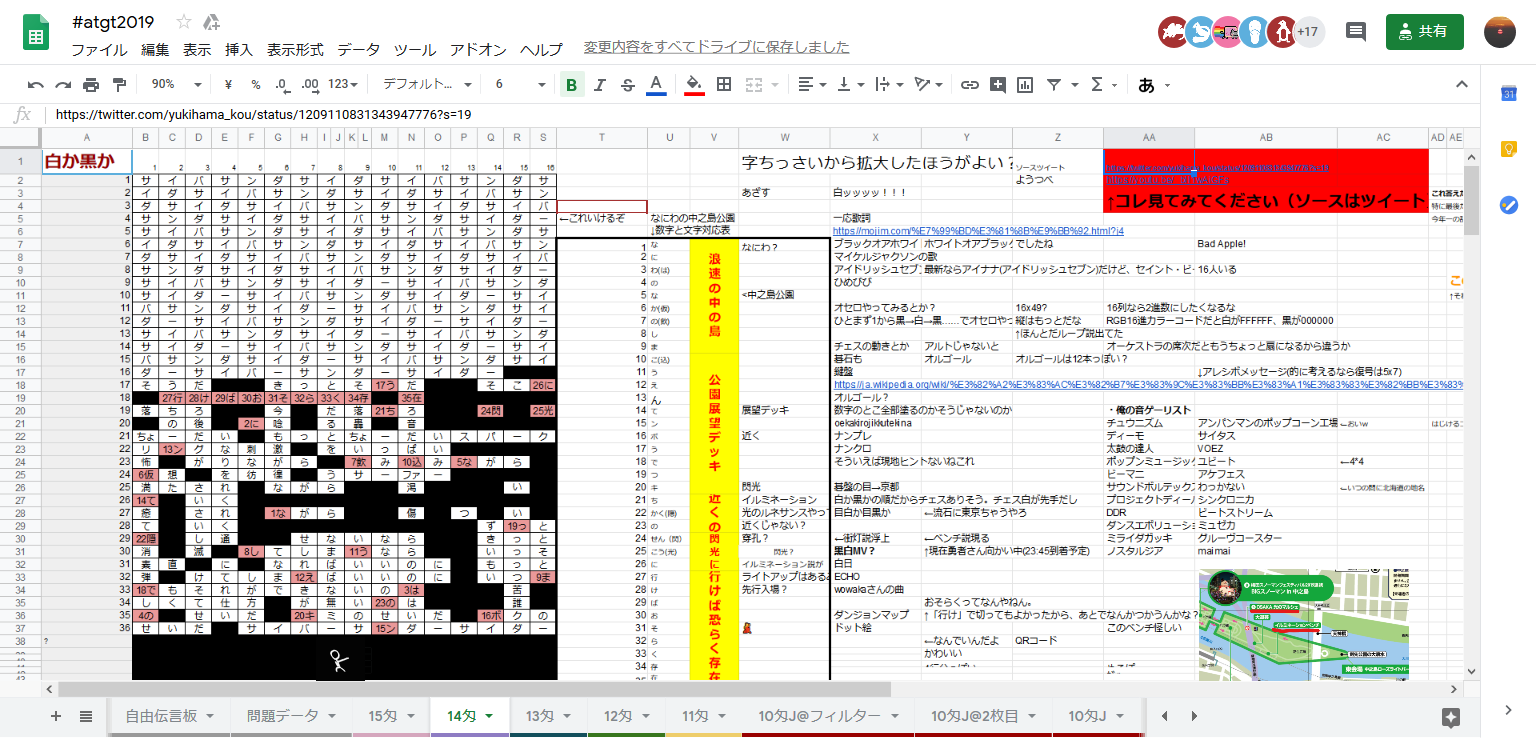
結果の処理

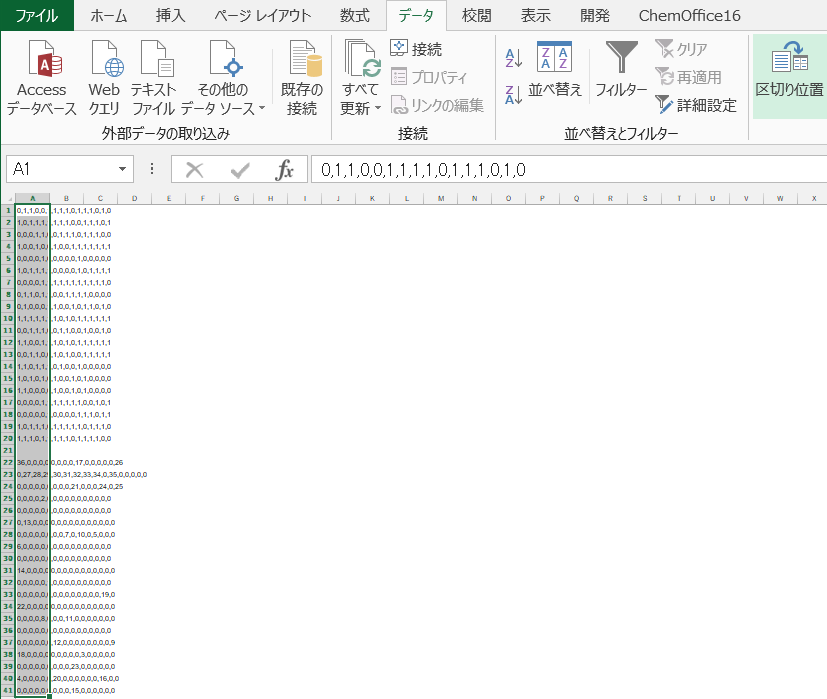
Excelを使う。

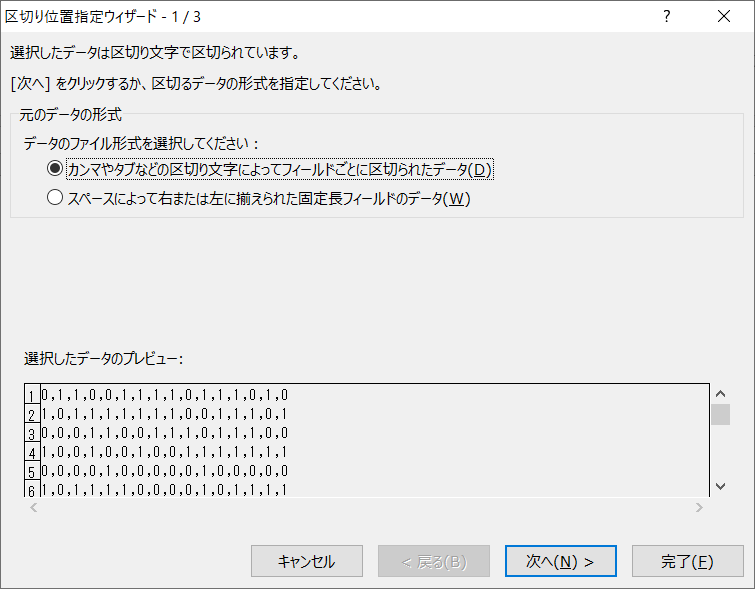
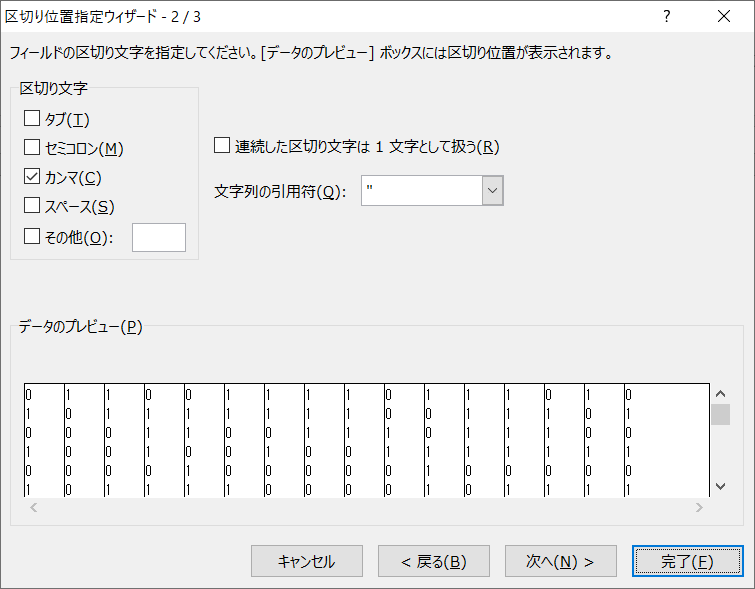
まずExcelに貼り付けて、区切り位置指定する

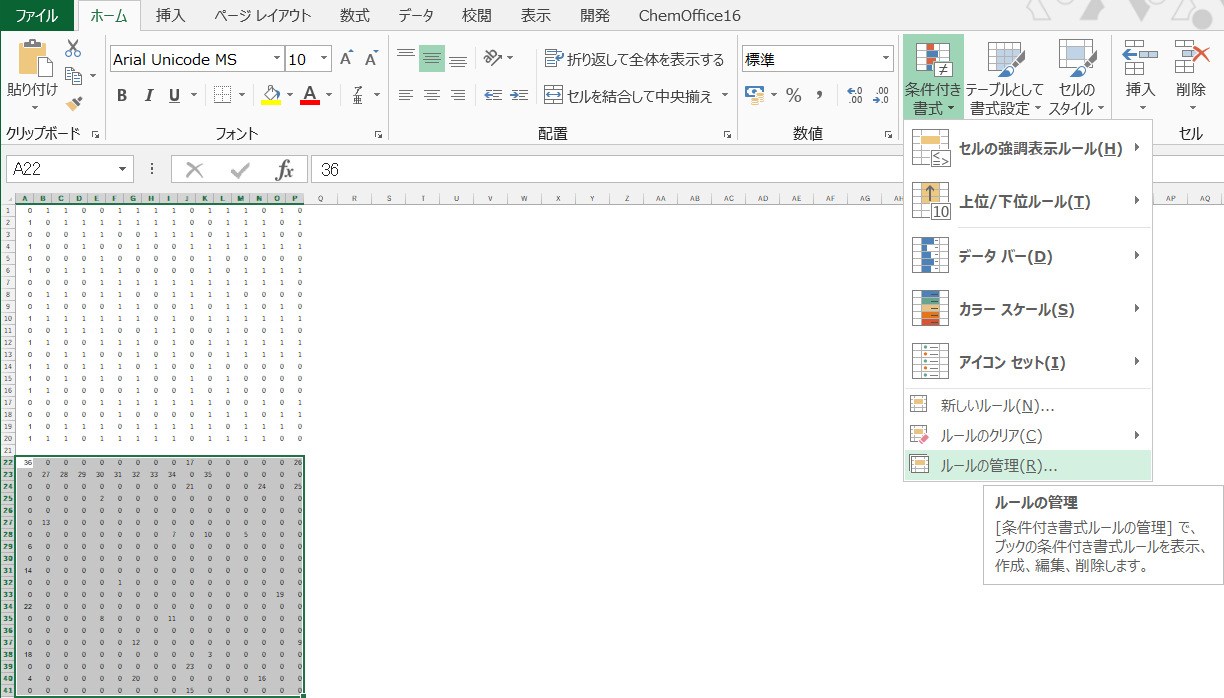
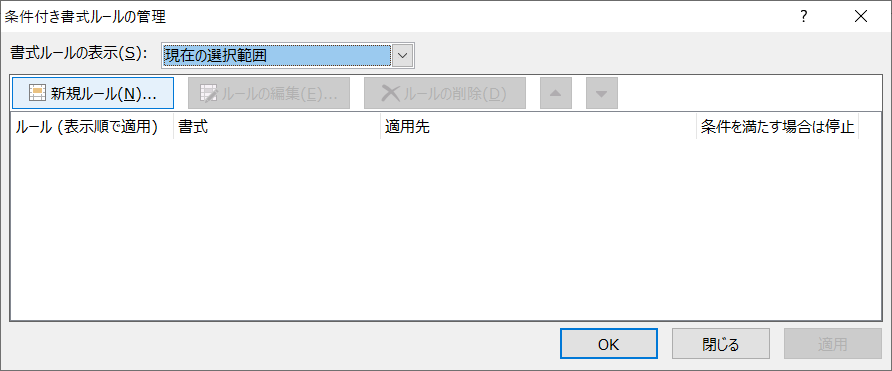
適当に列の幅を調整した後、下の表を選択して条件付き書式の設定をしていく。

条件付き書式は選択開始位置からの相対参照ができる。

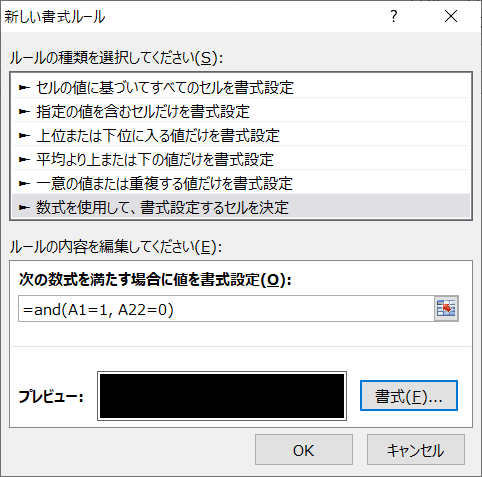
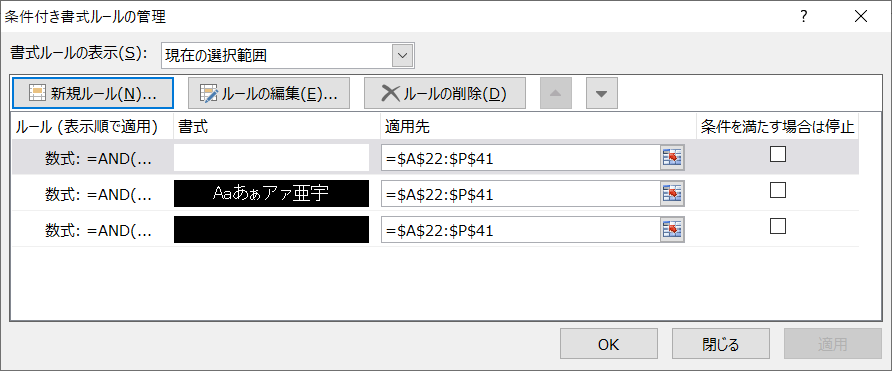
if関数で色分け。文字・背景色を変更して「赤字」で表示させる方法

上の表の対応する座標が1
- 下の表が0 → 背景も文字も黒
  =and(A1=1, A22=0)
- 下の表が0以外 → 背景は黒、文字は白
  =and(A1=1, A22<>0)
上の表の対応する座標が0
- 下の表が0 → 背景も文字も白
  =and(A1=0, A22=0)

こんな感じ

というわけでこんな結果を得る。

先を越された

1〜2　2〜3 ...　って反転させたけど。 pic.twitter.com/uCvWP37vlS
— たあ (@chakabou) December 23, 2019

Sub hanten()
    '選択範囲の座標取得
    x1 = Selection(1).Row
    y1 = Selection(1).Column
    x2 = Selection(Selection.Count).Row
    y2 = Selection(Selection.Count).Column


    For i = x1 To x2
        For j = y1 To y2
        If Cells(i, j).Interior.Color = 0 Then
            Cells(i, j).Interior.Color = 16777215 '白く塗る
        Else
            Cells(i, j).Interior.Color = 0             '黒く塗る
        End If

        Next
    Next

End Sub

そうとうスモールな半自動化による結果が先に飛び出てしまった。

(あれっ、でも私のと結果合わなくね？)

甜菜はそんなものをふっとばして答えにたどり着く

難航するかに見えたこの問題は、結論から言うと一人の甜菜によってすべてを吹き飛ばして答えにたどり着いた。

#atgt2019

完全に理解した

これサイバーサンダーサイダーのPVだ
— 雪浜皐 (@yukihama_kou) December 23, 2019

本日のは？件だ。どっからそれが飛び出てきた。

というかそもそも私はサイバーサンダーサイダーなんて知らない。何だそれは

【VY1】サイバーサンダーサイダー【オリジナル曲】 https://t.co/Yr55VajU8x #sm15440067 #ニコニコ動画 pic.twitter.com/zbggwnKoLw
— yumetodo-鳥の氷河から逃げる (@yumetodo) December 23, 2019

ボカロ殿堂入り楽曲らしい。すまんな、ボカロはわからん。

とにかくこの空白のパターンが合致する、かつ、問題用紙下側黒い16×4くらいのくろい部分の真ん中にある白い部分の説明がつくというのでスプシ班が一斉に動き始め怒涛の勢いで埋めた

スプシ班入力し始めたｗｗｗｗ #atgt2019 pic.twitter.com/xdDwp7AbzC
— リョウ（凌）@C97①ロビン？ (@fctokyo1016) December 23, 2019

#atgt2019 pic.twitter.com/d42TFBRNdZ
— MAGNET (@Magnet_Compass) December 23, 2019

まもなくスプシで答え出そうです #atgt2019 pic.twitter.com/50E8UKleL7
— リョウ（凌）@C97①ロビン？ (@fctokyo1016) December 23, 2019

#atgt2019

なんかおる pic.twitter.com/uDz2oMoxGG
— Masateo(スリープモード) (@masateo0414_v2) December 23, 2019

さっきのイベントの地図だけど記載ないけど閃光が近くにあるんかな#atgt2019 pic.twitter.com/8O9YjQcKF8
— つる (@crane628496) December 23, 2019

怪しいベンチ発見@tos #atgt2019 pic.twitter.com/44CE0O858D
— たか (@takafee) December 23, 2019

あったーーーーー！！ #atgt2019 pic.twitter.com/L8P5IKnElT
— 古井戸 (@deepandoldwell) December 23, 2019

#atgt2019 14匁にC++の力で挑んだが甜菜はそんなものをふっとばして答えにたどり着く