この文章
http://www.scholarpedia.org/article/Evolution_strategies の和訳です。文章のライセンスは CC BY-NC-SA 3.0 です。
概要
進化戦略(ES)は自然にインスパイアされた探索(と最適化)の一種です。突然変異や組み替えを使用する進化アルゴリズムに属します。より良い解を反復的に求めるために個体群から個体を選択します。1960年代中頃のドイツの Technical University of Berlin の P. Bienert, I. Rechenberg, H.-P. Schwefel に由来します。風洞の最小抗力体の理想的な形を求めるために生物にインスパイアされた手法を開発しました。
進化戦略は連続・離散・組合せ最適化を含む全ての領域で利用可能です。制約があってもなくても良いですし、これらの混合探索空間でも利用可能です。最適化問題の形式は、
y^* = \text{argopt}_{y \in Y} f(y)
の形式で与え、$f(y)$ が最適化すべき関数で、目的関数とも呼ばれます。これは、シミュレーションなど数学的な形で与えても良いですし、実世界から計測しても良いです。進化戦略は目的関数を集合で与えた、多目的最適化問題も解けます。
標準的な進化戦略
標準的な進化戦略はそれぞれ下記の記法で表記します。
(\mu/\rho,\lambda)-ES \\
(\mu/\rho+\lambda)-ES
$\mu$ は親の数です。$\rho < \mu$ は混ぜる数です(子供を生殖する際に関与する親の数です)。$\lambda$ は子供の数です。親は子供の集合から決定論的に選択されます(決定論的生存者選択)。カンマ選択の場合は子供から選ばれ、$\mu < \lambda$ でなければなりません。プラス選択の場合は親と子供を合わせた集合から選ばれます。選択は個体の適応度 $F(y)$ のランキングに基づいて $\mu$ 個、最善の個体を選びます。
一般的に進化戦略の個体は下記の方法で表記されます。
a := (y, s, F(y))
目的パラメータ $y \in Y$ が最適化すべき物です。$s$ は戦略パラメータで、自己適応進化戦略に必要です。$F(y)$ は観測された個体の適応度で、単純なケースでは目的関数と一緒で $F(y) = f(y)$ です。$F(y)$ が最適化すべき $f(y)$ に対して局所探索をした結果だったり、別の進化戦略の結果だったりする場合などで $F(y)$ と $f(y)$ を区別する必要があります。さらには、観測された $F(y)$ はノイズを含む $f(y)$ の結果だったりします。
$(\mu/\rho ; \stackrel{+}{,} ;\lambda)-ES$ のアルゴリズムの概要は下記の通りです。
$(\mu/\rho ; \stackrel{+}{,} ;\lambda)$ 自己適応進化戦略
- 親の個体群 $P_{\mu} = {a_1,\cdots,a_{\mu}}$ を初期化します。
- 下記方法で $\lambda$ 個の子供を作ります。$\tilde P _\lambda = \{ \tilde a _1, \cdots, \tilde a _\lambda \}$ 。
- $\rho$ 個の親をランダムに選びます。 $\rho = \mu$ ならば全て使います。
- $\rho$ 個の親を組み替えて個体 $r$ を作ります。
- $r$ の戦略パラメータ $s$ を突然変異します。
- $r$ の突然変異した戦略パラメータ $s$ を使用し、目的パラメータ $y$ を突然変異します。
- 決定論的選択で親を選びます。
- カンマ選択:子供の個体群 $\tilde P _\lambda$ より選択。
- プラス選択:子供 $\tilde P _{\lambda}$ と親 $P _{\mu}$ より選択。
- 終了条件を満たしていない場合は 2 に戻ります。
探索空間や目的関数次第で、組み替えや戦略パラメータは使用しなかったりします。例えば、 $(\mu/1 + \lambda)-ES$ つまり $(\mu + \lambda)-ES$ は組み替えを使用しません。これは、新しい $\mu$ 個の親を古い $\mu$ 個の親と $\lambda$ 個の子供から $F(y)$ に基づいて最善の $\mu$ 個を選ぶ方法です。
$(\mu/\rho + 1)$ タイプの進化戦略は定常状態進化戦略と呼ばれます。この方法は世代間のギャップがないです。各世代ごとに子供は1つだけ作り、適応度 $F(y)$ に基づいて最悪の個体が個体群から取り除かれます。個体の評価値の計算時間が定数時間で無い場合に並列計算したい場合は非同期並列処理が出来るので便利です。
終了条件としては、適応度の距離、探索空間の距離、世代数などが使えます。
例:自己適応進化戦略
進化戦略における突然変異と組み替えの設計は問題固有です。例として、無制約の実数値空間 $\mathbb{R}^n$ を探索する $(\mu/\mu_I,\lambda)$ 自己適応進化戦略を考えます。個体は $a = (y, \sigma, F(y))$ で定義されます。下記に基づいて $\lambda$ 個の子供が作られます。
\forall l=1, \ldots, \lambda : \;\; \mathbf{a}_l \leftarrow
\begin{cases}
& \sigma_l \leftarrow \langle \sigma \rangle
\mathrm{e}^{\tau \mathrm{N}_l(0,1)}, \\[2mm]
& \mathbf{y}_l \leftarrow \langle \mathbf{y} \rangle +
\sigma_l \mathbf{N}_l(\mathbf{0}, \mathbf{I}), \\[2mm]
& F_l \leftarrow F(\mathbf{y}_l),
\end{cases}
\qquad\qquad\mbox{(I)}
これはアルゴリズムの概要のステップ 2 と 3 に該当します(初期化・進化ループ・終了条件は含まれていません)。$\mathrm{N}_l(0,1)$ と $\mathbf{N}_l(\mathbf{0}, \mathbf{I})$ は (0, 1) 正規分布のスカラーとベクトルです。それぞれ、戦略パラメータ $\sigma$ と n 次元目的パラメータベクトル $\mathbf{y}$ の突然変異操作を実装しています。それぞれ $\langle \sigma \rangle$ と $\langle \mathbf{y} \rangle$ を組み替えた物に対して突然変異の操作を適用します。
突然変異した後の戦略パラメータ $\sigma_l$ は目的パラメータの突然変異の強さをコントロールします(この例では $\sigma_l$ は単に正規分布の標準偏差です)。突然変異は組み替え後の $\langle \mathbf{y} \rangle$ に加算されます。
(I) に基づいて突然変異の強さ $\sigma$ を変えることは、突然変異の強さの自己適応になります。なぜなら、個体の $\sigma_l$ は個体の $y_l$ の生成をコントロールし、適応度 $F(\mathbf{y})$ に基づいて特定の個体 $\mathbf{a}_l$ を選択することは、対応する $\sigma_l$ を引き継ぐことになるからです。この過程は $\sigma$ 自己適応とも呼ばれます。内部の戦略パラメータをモデルベースの外部のコントロールルールなしに自己適応進化戦略が動作することを意味します。
自己適応は学習パラメータ $\tau$ に依存します。経験的および理論的調査では $1 / \sqrt{n}$ に比例させることが推奨されています。例えば、$\tau = 1 / \sqrt{2n}$ です。
(I)の組み替えは最善な $\mu$ 個の子供の算術平均を使います。$a$ を個体 $\mathbf{a}$ の要素($\sigma$ や $\mathbf{y}$)とします。組み替え後の要素 $\langle a \rangle$ はこのように計算します。
\langle a \rangle := \frac{1}{\mu} \sum_{m=1}^{\mu} a_{m;\lambda},
\qquad\qquad\mbox{(II)}
$m;\lambda$ は(最新の世代の)上位 $m$ 番目の子供です。
この手の組み替えは、全体的中間の組み替えと呼ばれ、下付きの $I$ を混ぜる数の $\rho$ につけます。中間による組み替え以外にも、離散的な組み替えでは、親同士を軸ごとにランダムに組み替えたりもします。
Mathematica および Matlab/Octave の $(\mu/\mu_I, \lambda)$-$\sigma$ 自己適応進化戦略の簡単な実装は http://www2.staff.fh-vorarlberg.ac.at/~hgb/downloads.html からダウンロードできます。
(訳注:実験結果 http://qiita.com/yukoba/items/2dd4d254267f011af84d もご覧ください)
進化戦略のバリエーションと操作の設計原則
$(\mu/\mu_I,\lambda)$ は、等式 (I) において等方的分布による突然変異を目的パラメータベクトル $\mathbf{y}$ に対して適用しますが、より高度な進化戦略としては実数値探索空間内で相関性のある突然変異が出来るように、共分散行列適応 (CMA) 手法 (CMA-ES) を使用します。
さらには、階層構造進化戦略(メタ進化戦略、入れ子進化戦略とも呼ばれます)や捕食者-被食者進化戦略などが使われます。例えば、単純なメタ進化戦略はこのように定義されます。
\left[ \mu' / \rho' + \lambda' (\mu/\rho, \lambda)^\gamma \right]\mbox{-ES}
部分個体群 $\lambda'$ 個に対して、 $(\mu/\rho, \lambda)$-進化戦略を世代 $\gamma$ 回(分離された時間)独立に実行します。このような戦略は、混合構造や、パラメータ最適化タスクや、内側の進化ループの戦略パラメータ(個体数や突然変異パラメータ)の進化的学習に使われます。
特定の問題に対する進化戦略のパフォーマンスは進化戦略の操作(突然変異、組み替え、選択)の設計および進化の過程における進化戦略の適応方法(適応スキーム:σ自己適応、共分散行列適応など)に大きく依存しています。理想的には、進化過程全体においてシステムが進化可能であることを保証するように設計されるべきです。いくつか一般的な原則とガイドラインがあります。
- 選択は動植物に対してブリーダーが行うように行います。
- 連続空間でのカンマ選択の場合での典型的な $\mu / \lambda$ は 1/7 から 1/2 の間です。
- 有限の離散空間で、変異操作が全ての点に到達することを保証する場合、プラス選択を使用すると、有限の時間でグローバルな最適解に確率収束することを保証します。しかし、これは、無限時間走らせた結果であり、一般的な有限時間での結論は導き出せないです。
- 組合せ最適化問題ではプラス選択を使用することを推奨します。
- 進化は一般的には表現型レベルで設計します。問題文は、強因果関係の原理が保存される自然な方法で表現されるべきです。変異操作(突然変異と組み替え)は小さな探索ステップが評価値の小さな変化となるように(逆もしかり)なってないと行けないことを意味します。
- 変異操作(突然変異と組み替え)は最大エントロピー原理に基づいて設計されるべきです。
- 突然変異が変異の主要な源です。進化戦略は常に突然変異操作を含むべきです。突然変異は、到達可能性の制約条件を満たさなければなりません。全ての探索空間内の有限距離の点は有限回数のステップで到達可能でなければなりません。可能であれば、自己適応のために突然変異はスケーラブルであるべきです。最大エントロピー原理によると、探索空間が実数の場合は正規分布を、整数の場合は幾何分布を使用するべきです。
- 組み替えは可能であり、かつ、役に立つ場合に使用すべきです。$\rho$ = 2以上の親個体を使用して1つの組み替え個体を生成します。2より大きい場合はマルチ組み替えと言います。組み替えの主要な目的は親の共通コンポーネントを保存することです。役に立つ共通性を次の世代に残し、親の遺伝子のコンポーネントの破壊的影響を和らげることです(遺伝的修復効果)。
個別の問題では上記の全ての原則に従う必要はありません。これらの原則に反することは必ずしも悪い結果をもたらすわけではありません。
例:組合せ順列問題に対する単純な (μ+λ)-ES
$\mathbf{y}^* = \mathrm{argopt}_{\mathbf{y}} f(\mathbf{y})$ において $\mathbf{y}$ ベクトルが n 個の要素の順列を表現する最適化問題を考えます。例えば $\mathbf{y} = (1, 3, 9, 2, \ldots)$ が要素の順列です。セールスマンが都市を訪れる順番(巡回セールスマン問題)や全体のコスト $f(\mathbf{y})$ を最小にする仕事の順番のジョブスケジューリング問題だったりします。
進化戦略において、最適化問題は通常、自然な問題表現の方法で表現します。つまり、変異操作を $\mathbf{y}$ の順列に直接作用させます。
個体を $\mathbf{a} = (\mathbf{y}, F(\mathbf{y}))$ で定義します。進化戦略は $\lambda$ 個の子供を下記の方法で生成します。
\forall l=1, \ldots, \lambda : \;\;
\begin{cases}
& m \leftarrow \mbox{rand}\{1, \mu\}, \\[2mm]
& \mathbf{y}_l \leftarrow \mbox{PerMutate}( \mathbf{y}_{m; \, \mu+\lambda}), \\[2mm]
& F_l \leftarrow F(\mathbf{y}_l)
\end{cases}
これは、進化戦略のアルゴリズムの概要のステップ 2 と 3 に該当します。
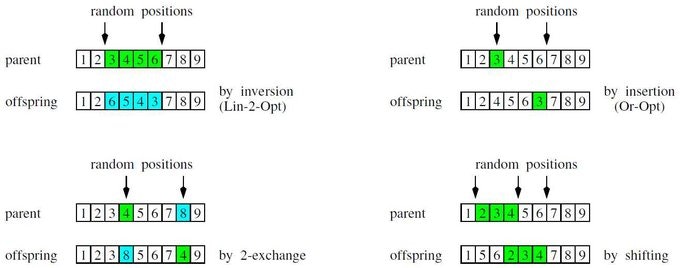
進化戦略は、1つ前の世代の親と子供の中の最善の $\mu$ 個の個体の中からランダムに親として選びます(これを $\mathbf{y}_{m; , \mu+\lambda}$ と表記します)。この親がランダムな順列で突然変異します。単純な順列操作を下記の図に記載しました。4つの順列操作:左上から右下へ、反転・挿入・2交換・シフト。
これらは、探索近傍(1ステップで到達できる状態)を定義する基礎的な移動ステップを表現しています。連続探索空間での突然変異とは異なり、(可能な最小の突然変異を表現する)最小の探索ステップが必ず存在します。異なる順列操作のパフォーマンスは解くべき最適化問題に依存します。強因果関係の原理(小さなステップが小さな適応度の変化)を保証しようとすることが、これらの操作の主要な設計および選択原理の1つです。
共分散行列適応進化戦略 CMA-ES
CMA-ES は実数値 $\mathbb{R}^n$ 探索空間に対する最高水準の進化的最適化です。CMA-ES は A. Gawelczyk, N. Hansen, A. Ostermeier らに1990年代中頃に提案されました。
$(\mu/\mu_I, \lambda)$-$\sigma$ 自己適応進化戦略との基本的な違いは、突然変異の分布が共分散行列 $\mathbf{C}$ から生成されることで、これは進化中に適応していきます。それゆえ、突然変異は適応度の局所的な地形に適応し、それゆえ最適解へ飛躍的に速く収束します。内部の戦略パラメータ(共分散行列 $\mathbf{C}$ とグローバルステップサイズ $\sigma$)をコントロールするのに、世代ごとに蓄積していく特殊な統計処理を行います。この部分が、(突然変異で変化する) $\sigma$ 自己適応の方法と異なります。
個体群の大きさ $\lambda$ が小さい時(小さいというのは、探索空間の次元 n に比べて小さいという意味です)、$(\mu/\mu_I, \lambda)$ CMA-ES の子供の更新公式を簡単に(しかし十分動きます)記述すると以下の通りです。
$(\mu/\mu_I, \lambda)$-CMA-ES
\mbox{(L1):} \quad
\forall l=1, \ldots, \lambda : \;\;
\begin{cases}
& \mathbf{w}_l
\leftarrow \sigma \sqrt{ \mathbf{C} } \,
\mathbf{N}_l(\mathbf{0}, \mathbf{1})\\[2mm]
& \mathbf{y}_l \leftarrow \mathbf{y} + \mathbf{w}_l \\[2mm]
& F_l \leftarrow F(\mathbf{y}_l)
\end{cases}
\mbox{(L2):} \quad
\mathbf{y} \leftarrow \mathbf{y} + \langle \mathbf{w} \rangle
\mbox{(L3):} \quad
\mathbf{s} \leftarrow \left(1-\frac{1}{\tau}\right)\mathbf{s}
+ \sqrt{\frac{\mu}{\tau} \left(2-\frac{1}{\tau}\right)} \,
\frac{\langle \mathbf{w} \rangle}{\sigma}
\mbox{(L4):} \quad
\mathbf{C} \leftarrow
\left(1-\frac{1}{\tau_{\mathrm{c}}}\right)\mathbf{C}
+ \frac{1}{\tau_{\mathrm{c}}} \mathbf{s} \mathbf{s}^T
\mbox{(L5):} \quad
\mathbf{s}_\sigma
\leftarrow \left(1-\frac{1}{\tau_\sigma}\right) \mathbf{s}_\sigma
+ \sqrt{\frac{\mu}{\tau_\sigma}
\left(2-\frac{1}{\tau_\sigma}\right)} \,
\langle \mathbf{N}(\mathbf{0}, \mathbf{1}) \rangle
\mbox{(L6):} \quad
\sigma \leftarrow \sigma\exp\left[
\frac{\| \mathbf{s}_{\sigma} \|^2 - n}
{2 n \sqrt{n} }
\right]
(L1) において、$\lambda$ 個の子供 $\mathbf{y}_l$ は正規分布の乱数ベクトルを変換行列 $\sqrt{\mathbf{C}}$ を使って変換して生成します。変換行列は共分散行列 $\mathbf{C}$ を $\sqrt{\mathbf{C}} \sqrt{\mathbf{C}}^T = \mathbf{C}$ でコレスキー分解した物と、グローバルステップサイズの $\sigma$ から作ります。
(L2) において、突然変異した物のうち最善の $\mu$ 個の個体を等式 (II) に基づいて組み替えて、次の世代の組み替え後の個体 $\mathbf{y}$ (重心)を作ります。アルゴリズム上、組み替え後の個体は1つです(これがアルゴリズム終了時の最終的な解になります)。
ベクトル $\langle \mathbf{w} \rangle$ は連続する2つの世代の組み替え後の個体をつなぎます。それゆえ $\langle \mathbf{w} \rangle/\sigma$ は探索空間内の進化の傾向を表現します。この情報は $\mathbf{s}$ ベクトルに蓄積されます(初期値は $\mathbf{s} = \mathbf{0}$ です)。時定数 $\tau=\sqrt{n}$ に従って指数関数的に減衰します。ベクトル $\mathbf{s}$ の方向は、時定数 $\tau_{\mathrm{c}} \propto n^2$ を使い、共分散行列 $\mathbf{C}$ (初期値は $\mathbf{C} = \mathbf{1}$ です) を更新(ランク1の更新)します。
残りの (L5) と (L6) は蓄積されたステップサイズ適応 (CSA) 手法と時定数 $\tau_\sigma = \sqrt{n}$ (初期値は $\mathbf{s}_\sigma = \mathbf{0}$)を使い、グローバルステップサイズ $\sigma$ をコントロールします。組み替え後の $\langle \mathbf{N}(\mathbf{0}, \mathbf{1}) \rangle$ は等式 (II) を使い計算します。
Mathematica および Matlab/Octave での CMA-ES の簡単な実装は http://www2.staff.fh-vorarlberg.ac.at/~hgb/downloads.html からダウンロードできます。
CMA-ES で個体群の大きさが大きい場合
CMA-ES で個体群の大きさが大きい場合、(L4) での共分散行列 $\mathbf{C}$ の更新方法が変わります。(L4) は下記に比例するようにランク $\mu$ の更新になります。
\frac{1}{\mu \sigma^2} \sum_{m=1}^\mu
\mathbf{w}_{m;\lambda} (\mathbf{w}_{m;\lambda})^T
この更新を最大限活用するには時定数 $\tau$, $\tau_{\mathrm{c}}$, $\tau_\sigma$ はそれように選ばれていないと行けないです。(詳細は Hansen, N. and Müller, S.D. and Koumoutsakos, P. (2003) をご覧ください)
(訳注:僕には CMA-ES の解説が少し間違っている気がします。本家の http://www.cmap.polytechnique.fr/~nikolaus.hansen/cmaesintro.html を読まれることをお薦めします)
参考文献
- Beyer, H.-G. and Schwefel, H.-P. (2002). Evolution Strategies: A Comprehensive Introduction. In ''Natural Computing,'' 1(1):3-52.
- Beyer, H.-G. (2001). The Theory of Evolution Strategies. Natural Computing Series. Springer, Berlin 2001.
- Hansen, N. and Ostermeier, A. (2001). Completely Derandomized Self-Adaptation in Evolution Strategies. In ''Evolutionary Computation,'' 9(1):159-195.
- Hansen, N. and Müller, S.D. and Koumoutsakos, P. (2003). Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). In ''Evolutionary Computation,'' 11(1):1-18.
- Rechenberg, I. (1994). Evolutionsstrategie '94. Frommann-Holzboog Verlag, Stuttgart, (in German).
- Schwefel, H.-P. (1995). Evolution and Optimum Seeking. Wiley, New York, NY.
訳注Tips
この文章では、連続値と言うこともあり、個体の全ての要素 $n$ 個を変異させていますが、個体が $n$ 個の離散値で構成されている場合は、1回の突然変異では変異させるのは1カ所の方が上手く行く事が多いです。その上で、親や子どもの数は $O(n)$ にします。人間の DNA には60億ヌクレオチドあり、 https://www.afpbb.com/articles/-/2805898 によると30~100個程度変異し(つまり変異率は1億分の1)、人口が70億人であり、つまり、n=60億の、同じ感じのスケール感です。
その上で、離散も連続も計算量は $O(n^2)$ になります。勾配法の計算量は $O(n)$ ですが、その代わり、最小値ではなく極小値に行く確率が高いです。メタヒューリスティクスな最適化アルゴリズムの多くは $O(n^2)$ だと思います。書籍『組合せ最適化』によると、巡回セールスマン問題の局所探索は $O(n^{2.2})$ だそうです。