進化戦略を実数パラメータの最適化問題に適用した場合の実験例です。進化戦略とは何かというのは、 http://qiita.com/yukoba/items/ed40e0c4f4a27b73c6b8 をご覧ください。
実数パラメータの最適化問題の最も簡単な問題例として、線形回帰のパラメータの最適化を本記事では採用しました。進化戦略は例えば組合せ最適化と実数パラメータの最適化を同時に行えたりなど、もっと複雑な問題に良さが出るのですが、線形回帰のパラメータの最適化には、他にもっと良い方法があるので、この例題は実用性はないです。
データセットは、scikit-learn のボストン住宅価格データセットを使いました。入力は13次元の実数ベクトル、出力は実数です。なのでパラメータは ax + b の a が13個、bが1個の合計14個です。
ソースコード
実験のソースコードは https://github.com/yukoba/EvolutionStrategyLinearModel をご覧ください。
厳密解
線形回帰なので厳密解が求まります。$R^2$ の最大値は 0.740607742865 です。
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
(x, y) = load_boston(True)
lr = LinearRegression()
lr.fit(x, y)
print(lr.score(x, y))
比較対象
全て自己適応進化戦略です。
| 名称 | 選択 | 交叉 | 戦略パラメータの交叉 | 戦略パラメータ数 | τ |
|---|---|---|---|---|---|
| 方式1 | + | 確率0.8 | 片方 | 14 | 1/sqrt(2) |
| 方式2 | + | 確率0.8 | 平均 | 14 | 1/sqrt(2) |
| 方式3 | + | なし | 交叉なし | 14 | 1/sqrt(2) |
| 方式4(最善) | + | 確率0.8 | 片方 | 14 | 1/sqrt(2*14) |
| 方式5 | + | 確率0.8 | 平均 | 1 | 1/sqrt(2*14) |
| 方式6 | , | 確率0.8 | 片方 | 14 | 1/sqrt(2) |
| 方式7 | + | 確率0.8 | 平均 | 14 | 1/sqrt(2*14) |
事前の予備調査で方式1が最善かなと予想していたので、(全て試すと組合せ爆発するので)それからずらした形で調査しました。しかし記事を書いているうちに方式4が最善であることが分かりました。
子孫数は全て30です。パラメータの初期値は平均0・分散1の正規分布です。戦略パラメータの初期値は0.1です。
- 選択:プラス選択(+)は親と子孫を両方残して最善100個体残す方法です。カンマ選択(,)は親を残さず子孫の中から上位10個を次世代の親としています。評価回数を固定にするため、子孫数は30で統一しています。
- 交叉:確率0.8とは、80%の確率で交叉あり、20%の確率で交叉なし(親1つ)の意味です。交叉する場合は親は2つです。パラメータは、2つの親から50%ずつの確率で選んでいます。
- 戦略パラメータの交叉:交叉する際に、「片方」は、2つの親から、パラメータを選んだ方の戦略パラメータを採用する方法です。「平均」とは、2つの親の戦略パラメータの平均を使います。
- 戦略パラメータ数:14とはパラメータと同数の戦略パラメータを使うという意味です。1とは戦略パラメータは1つにして使い回しするという意味です。
- τ:戦略パラメータの変化する速さです。
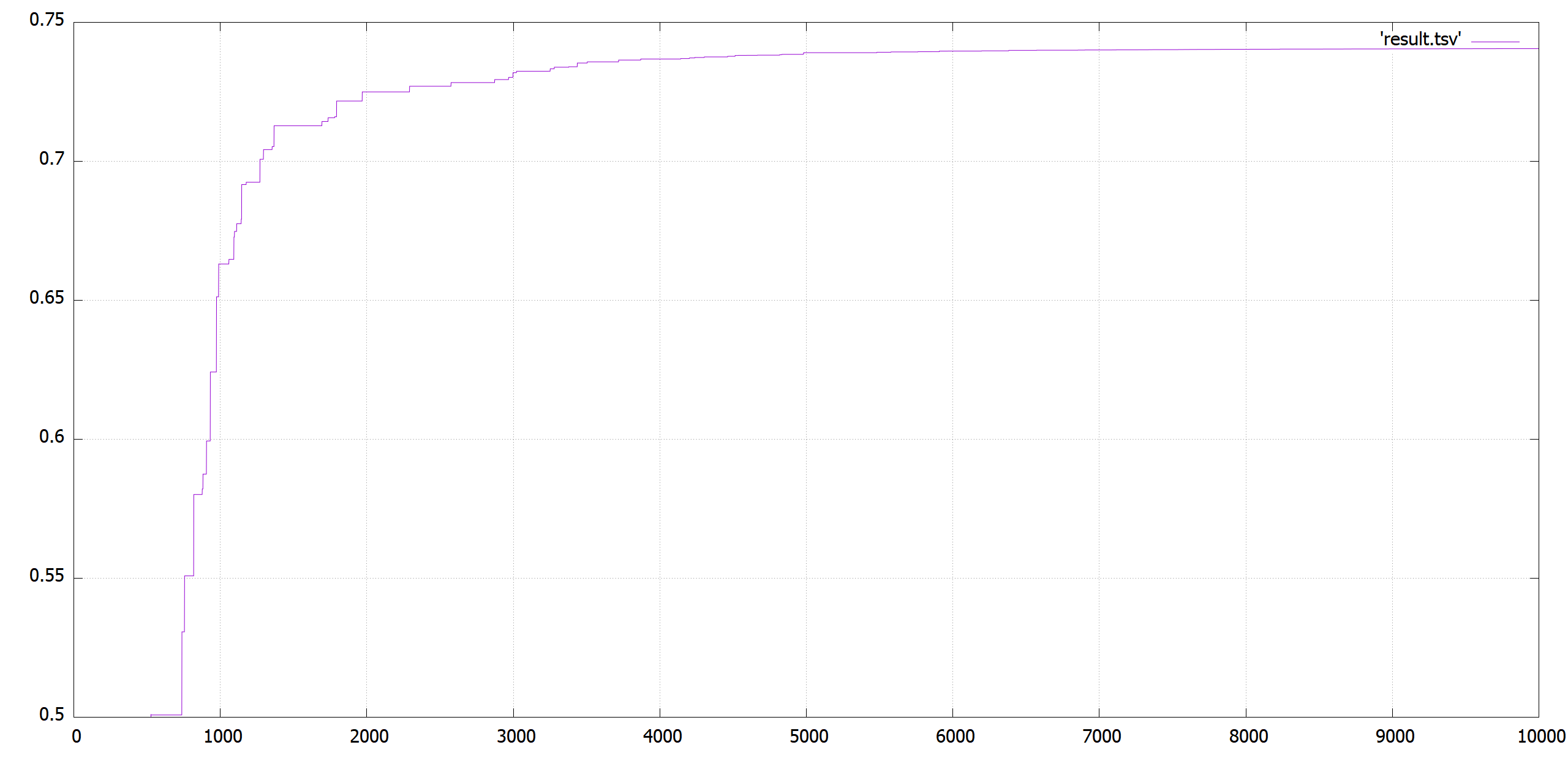
収束の様子
方式1では、このような感じで厳密解の 0.74 に収束していきます。
実験結果
どの $R^2$ に収束するかは確率的事象なので、100回行いヒストグラムにしました。反復回数1,000回と10,000回を調査しました。
反復回数1,000回
まだ収束する前の反復1,000回の段階では最善は方式1です。
|方式1|方式2|
|-----|-----|----|
|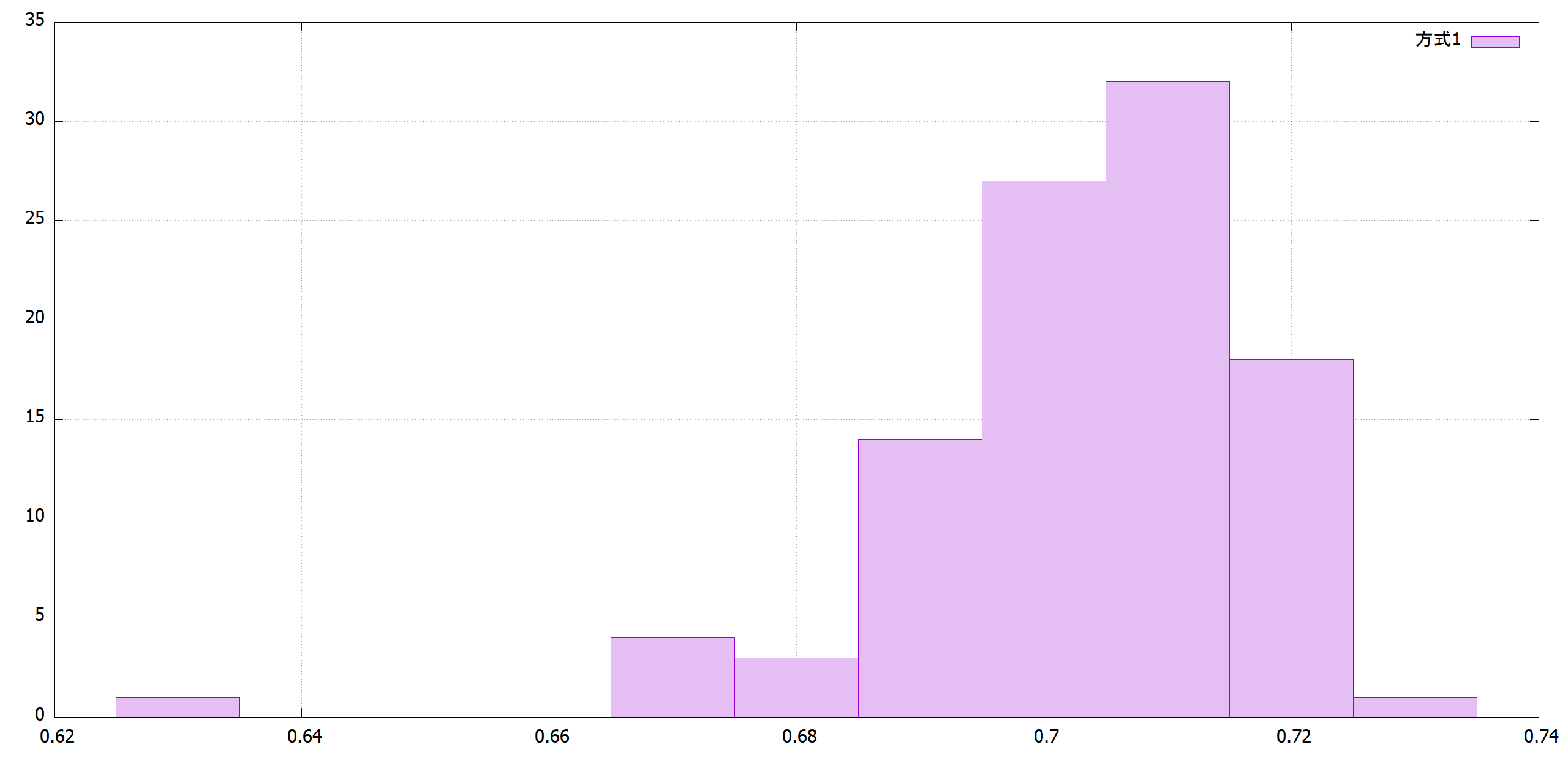 |
|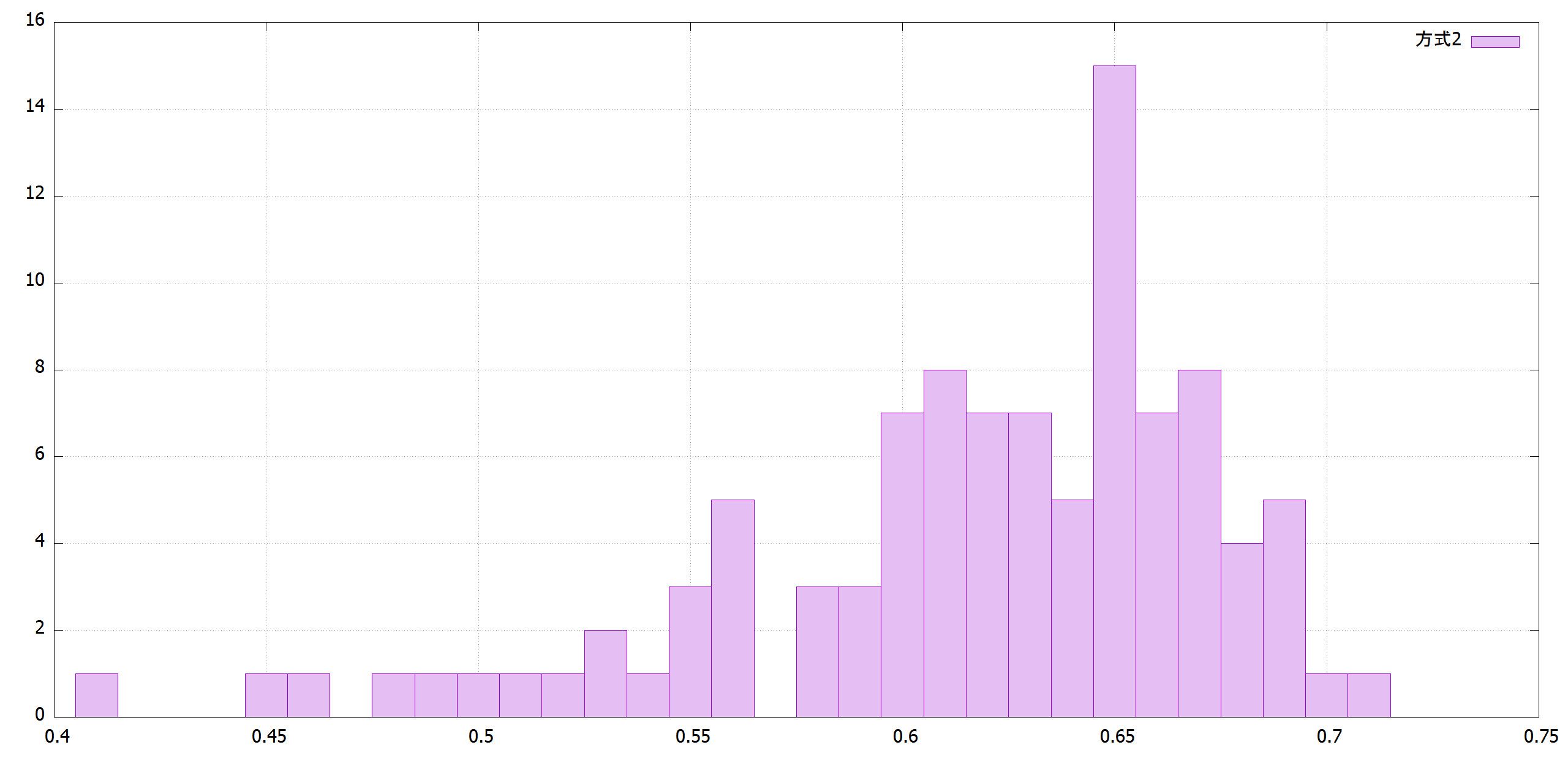 |
|
|方式3|方式4|
|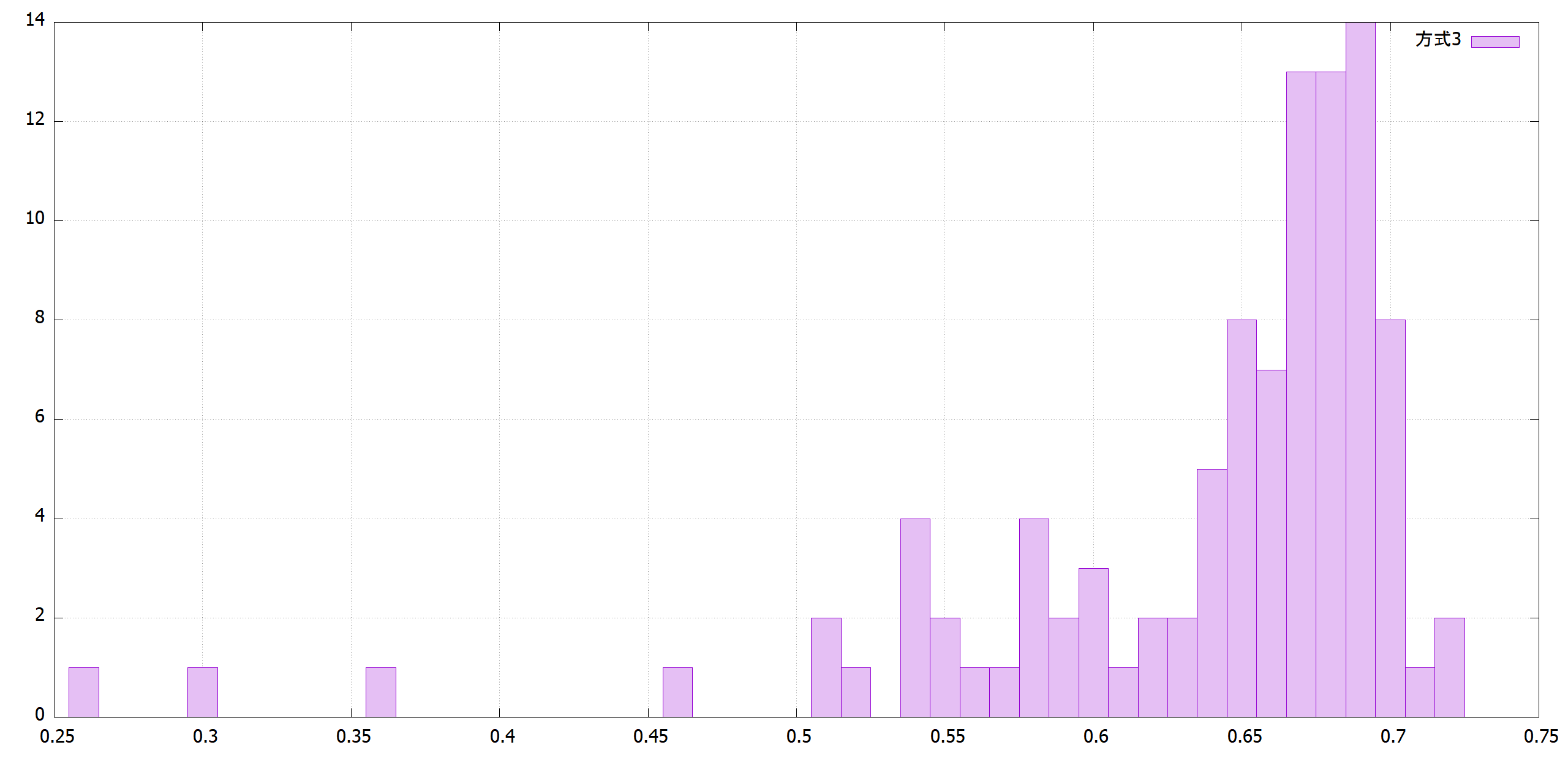 |
|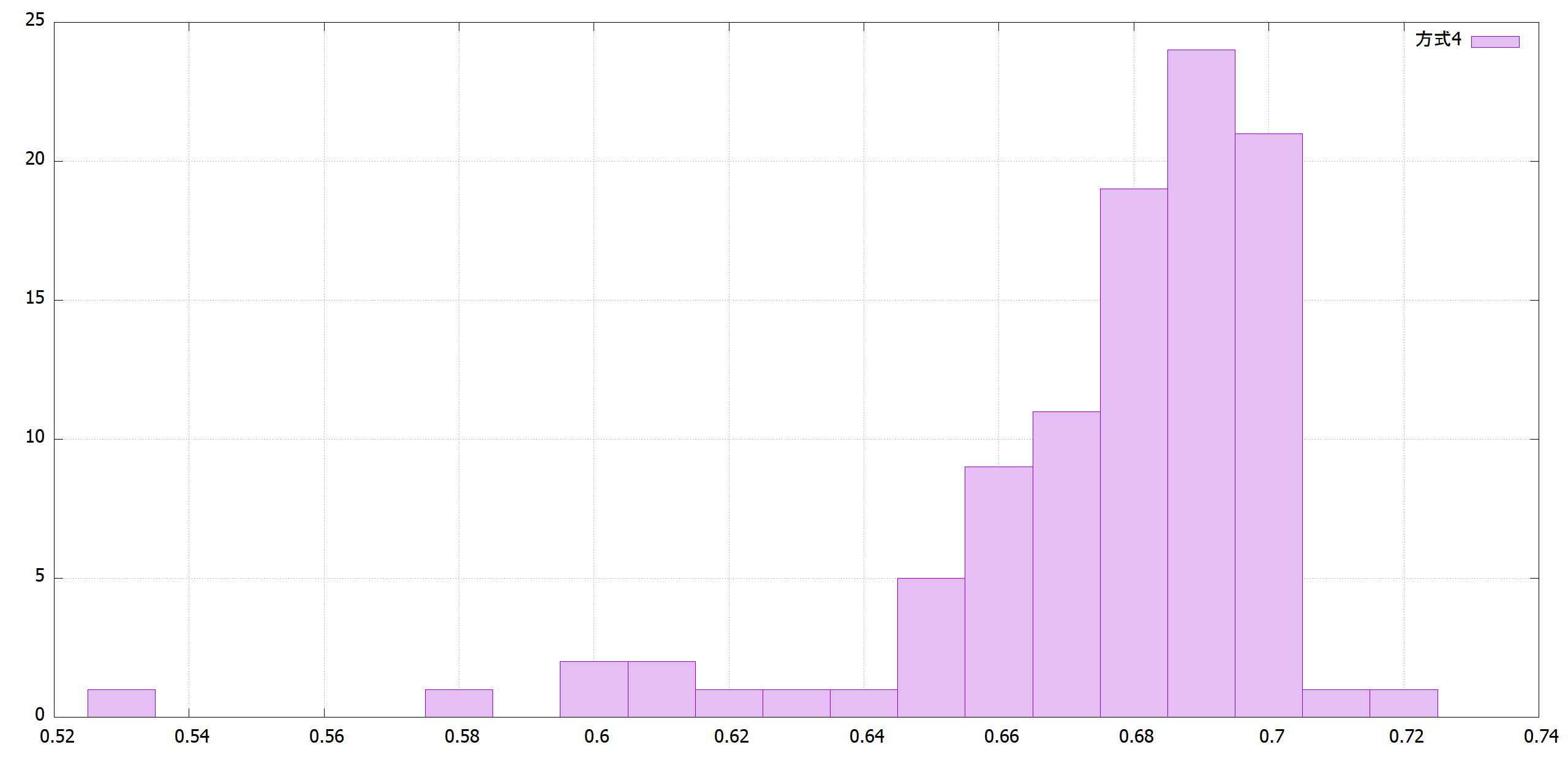 |
|
|方式5|方式6|
|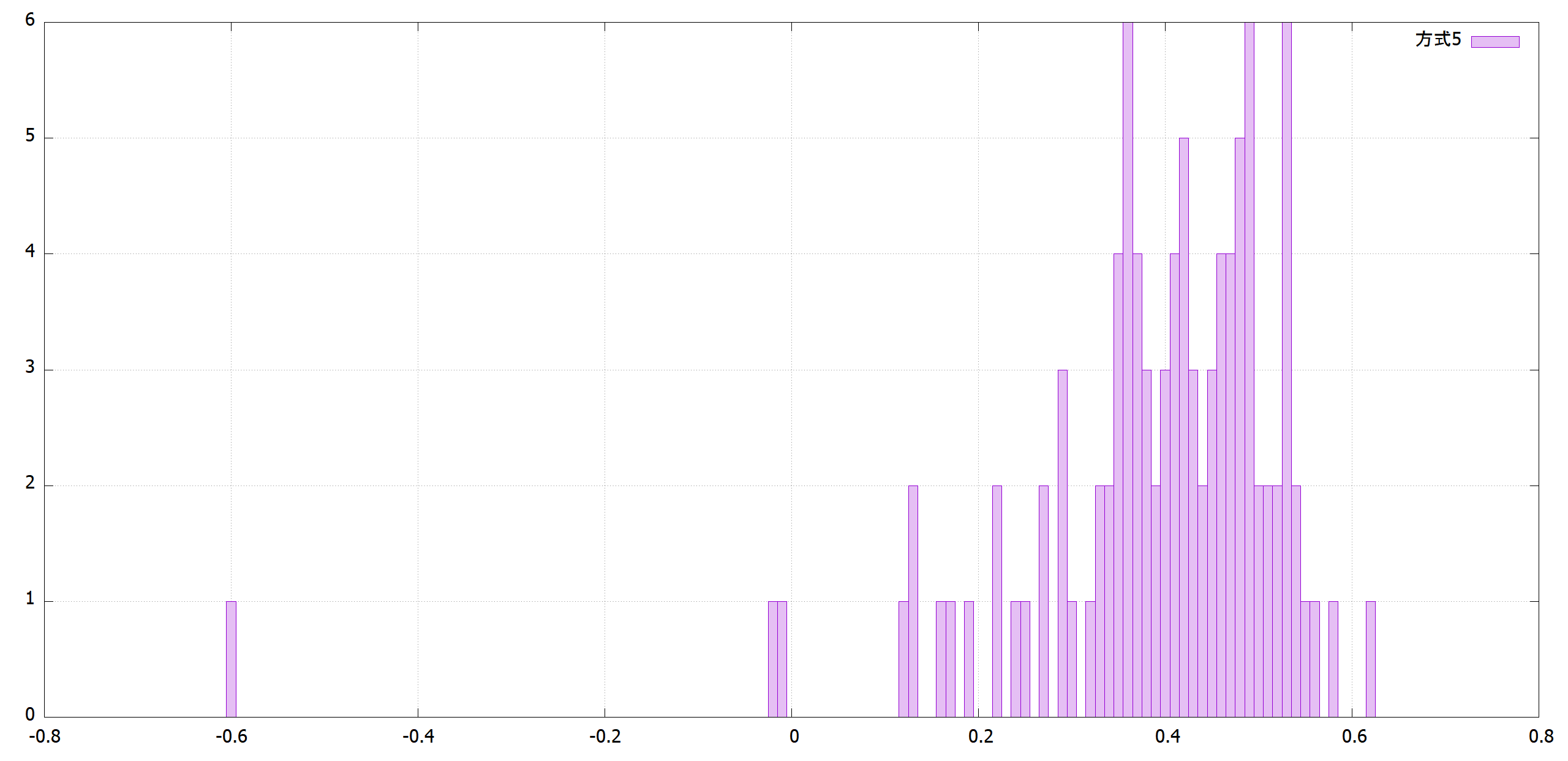 |
|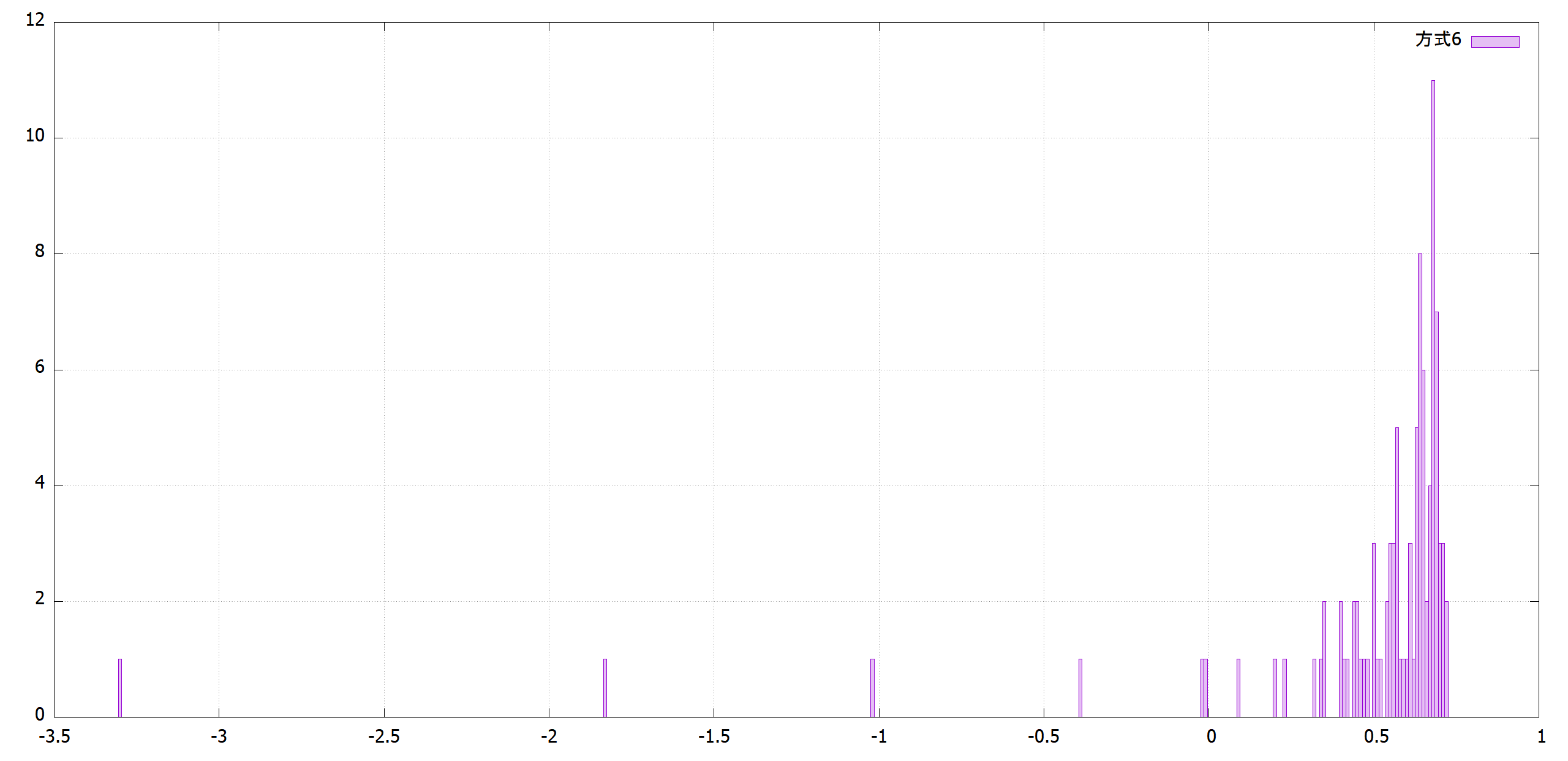 |
|
|方式7||
|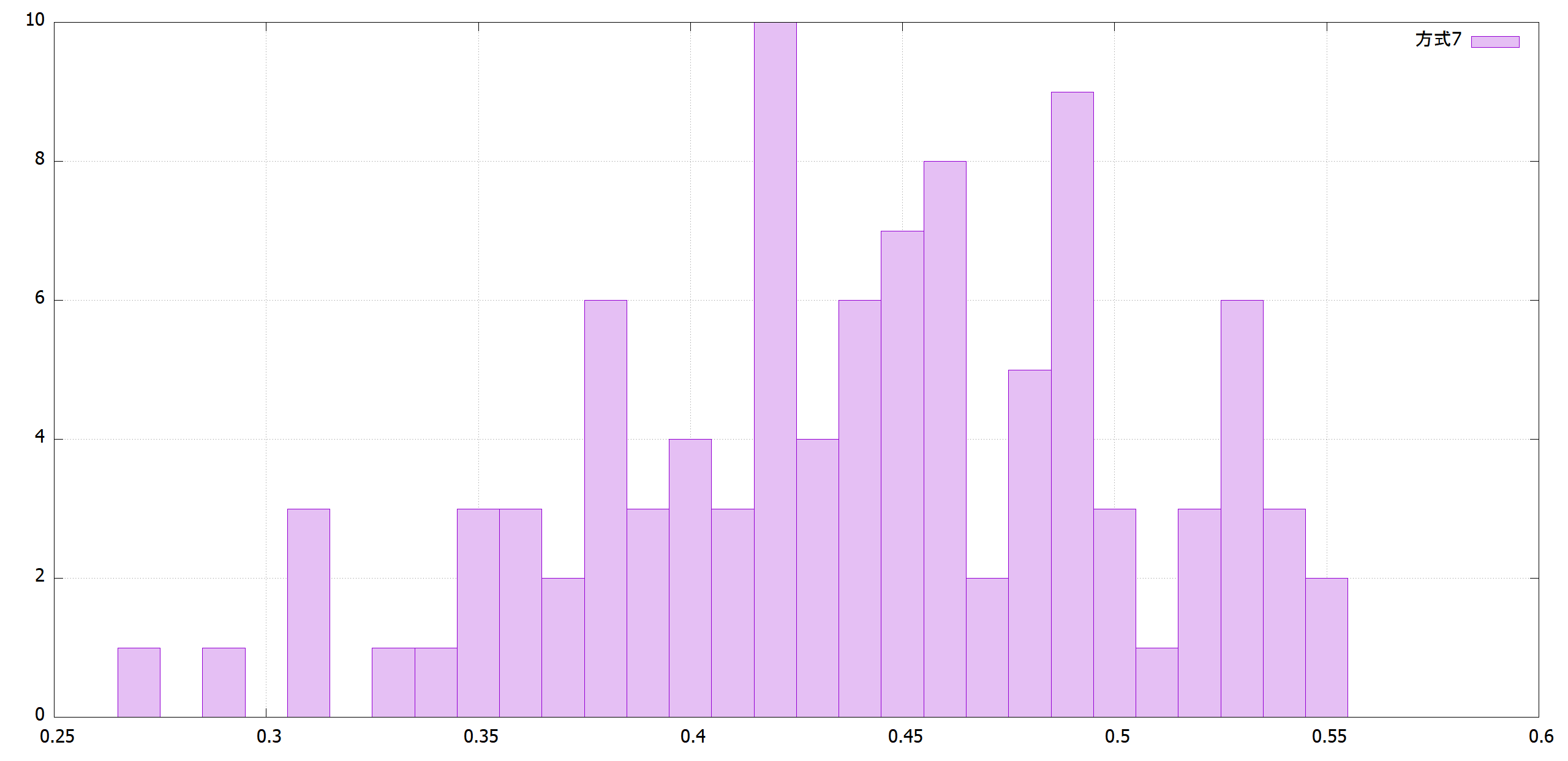 ||
||
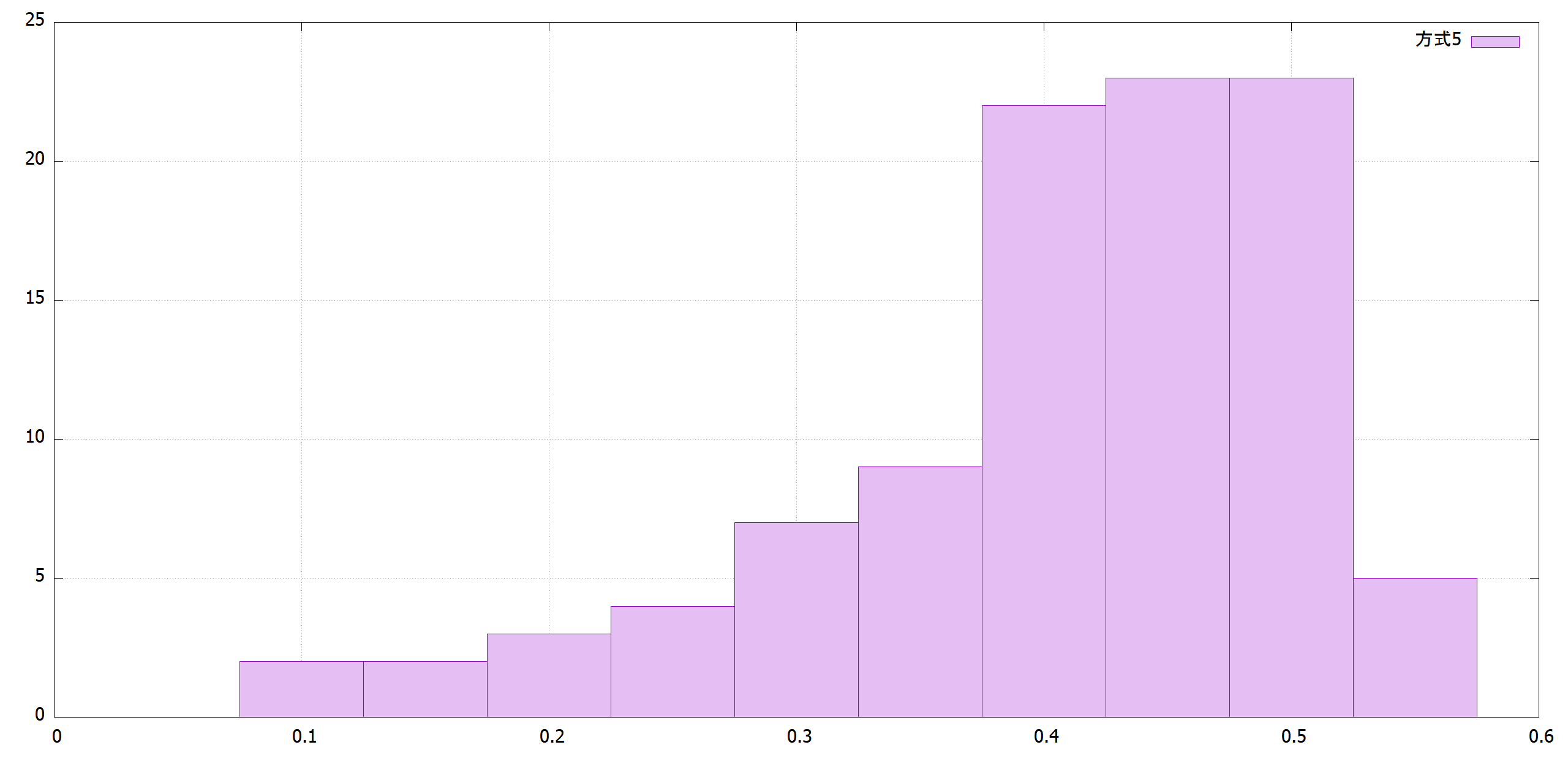
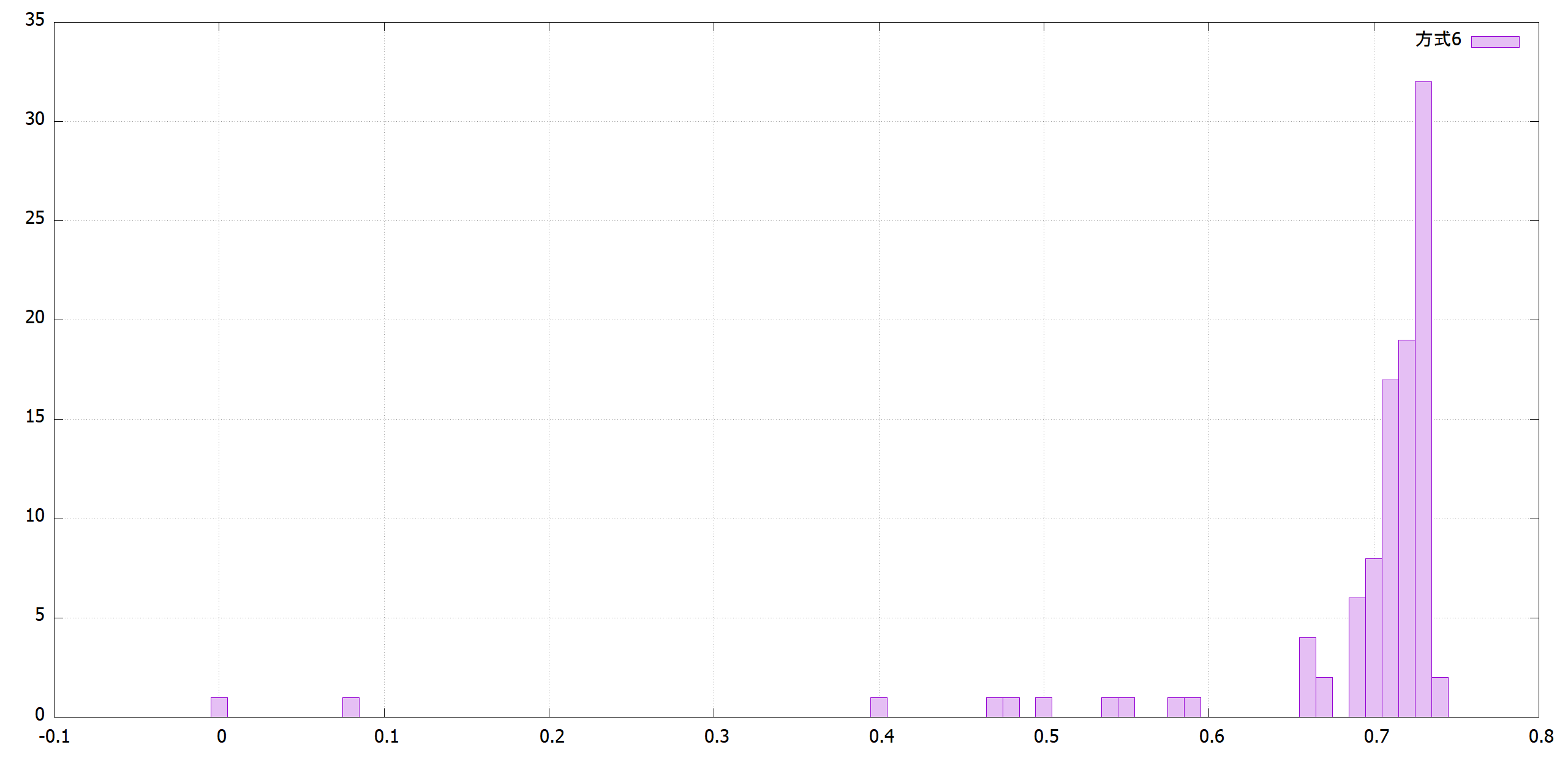
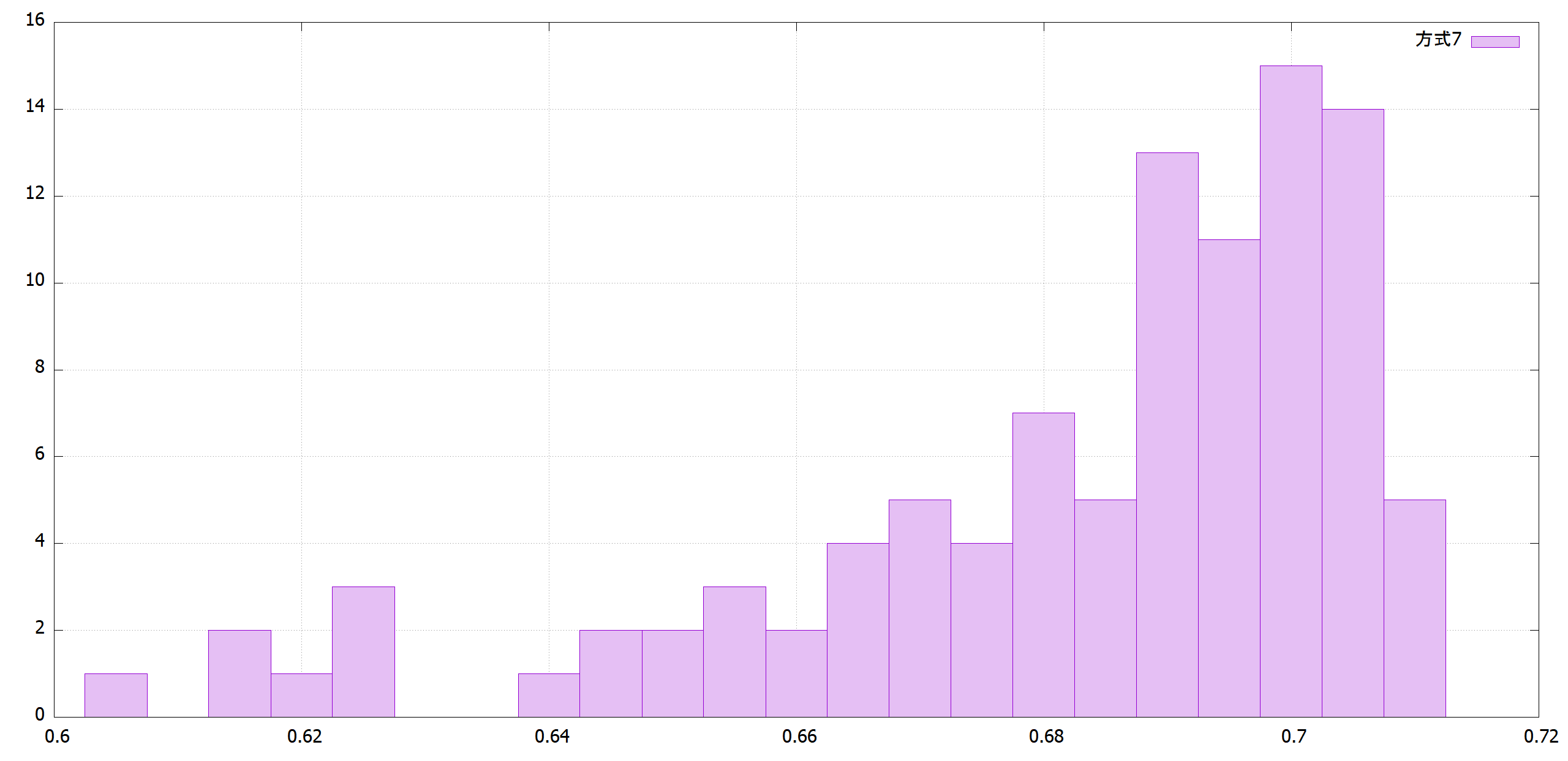
反復回数10,000回
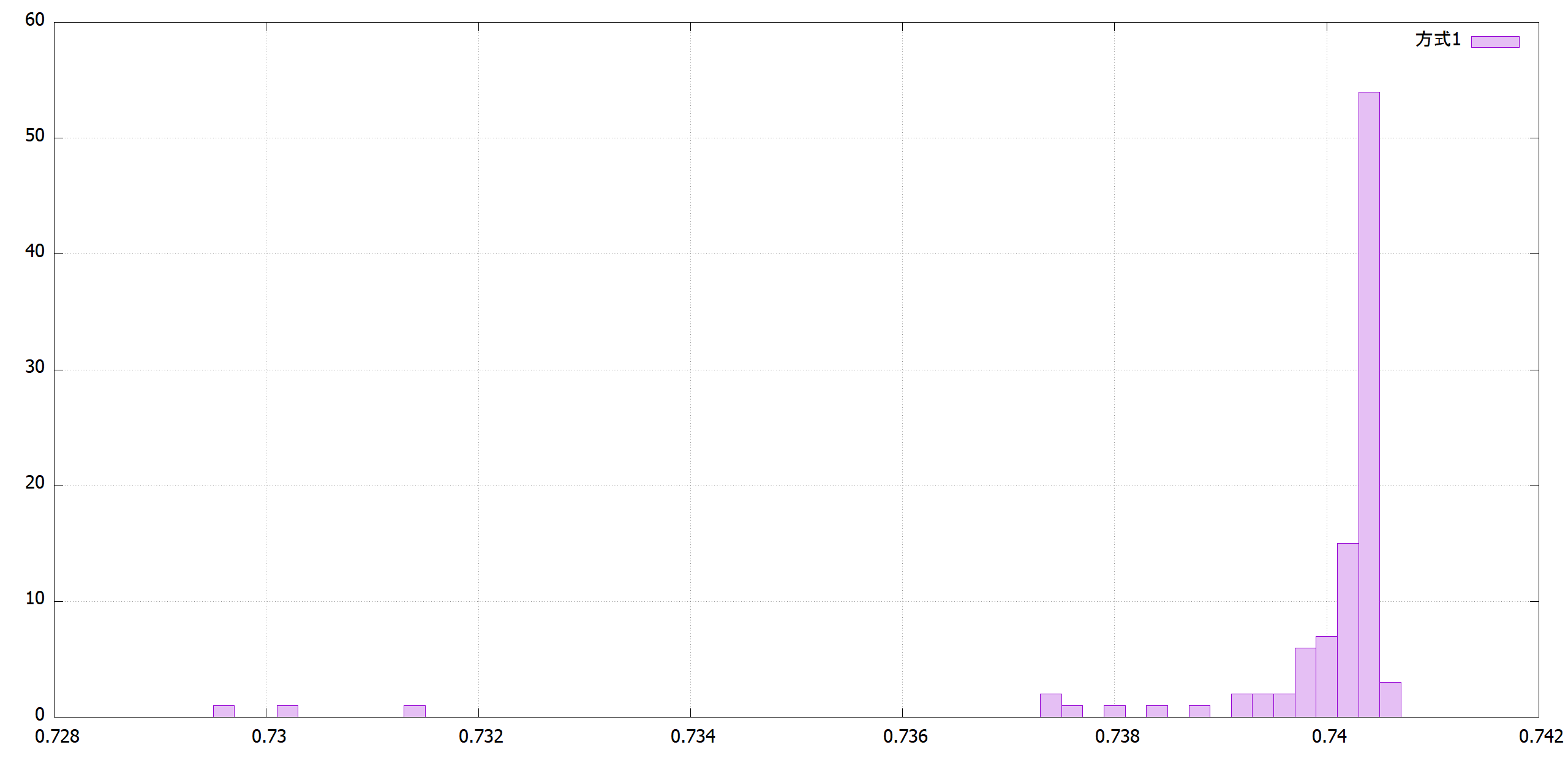
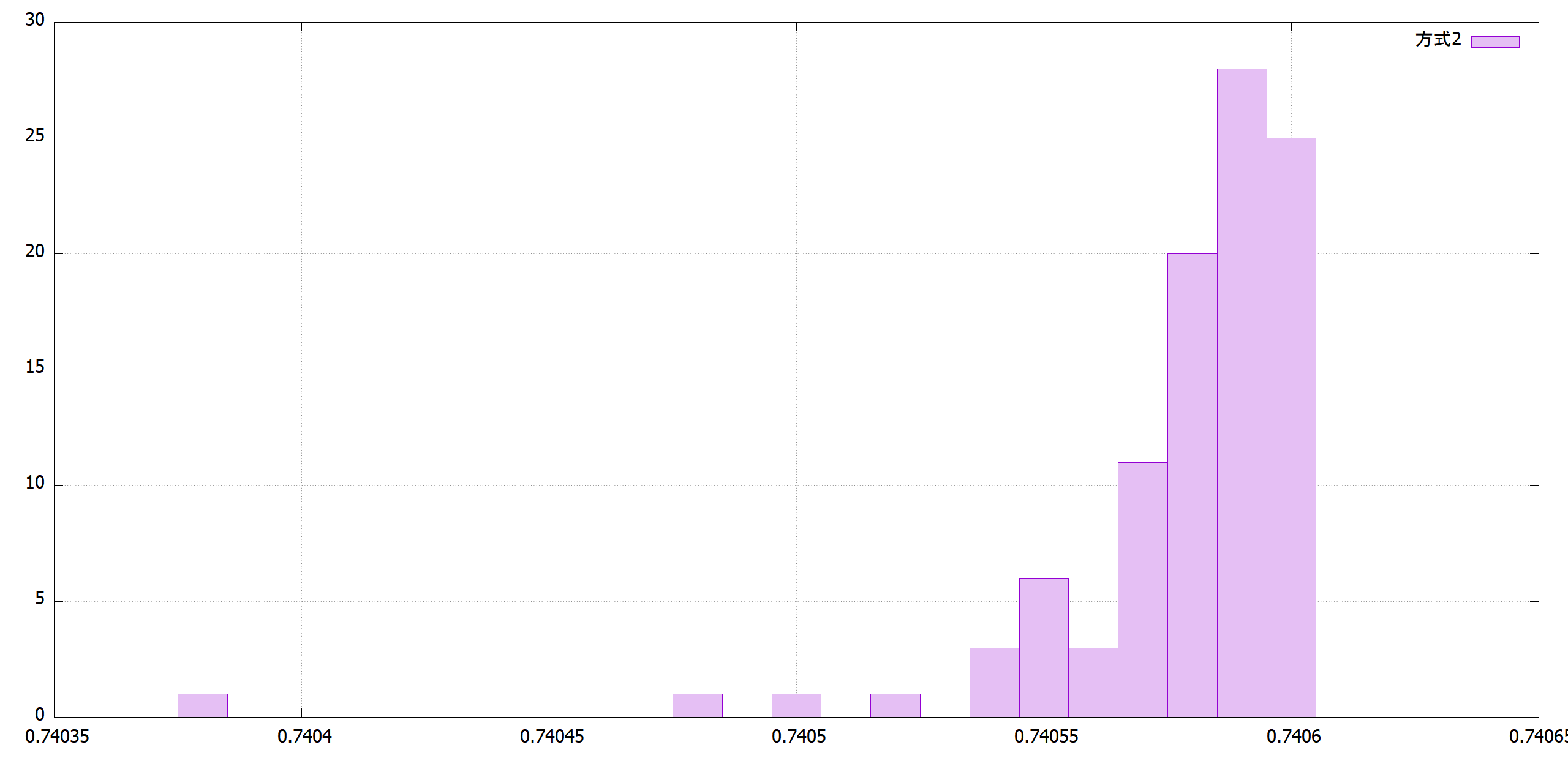
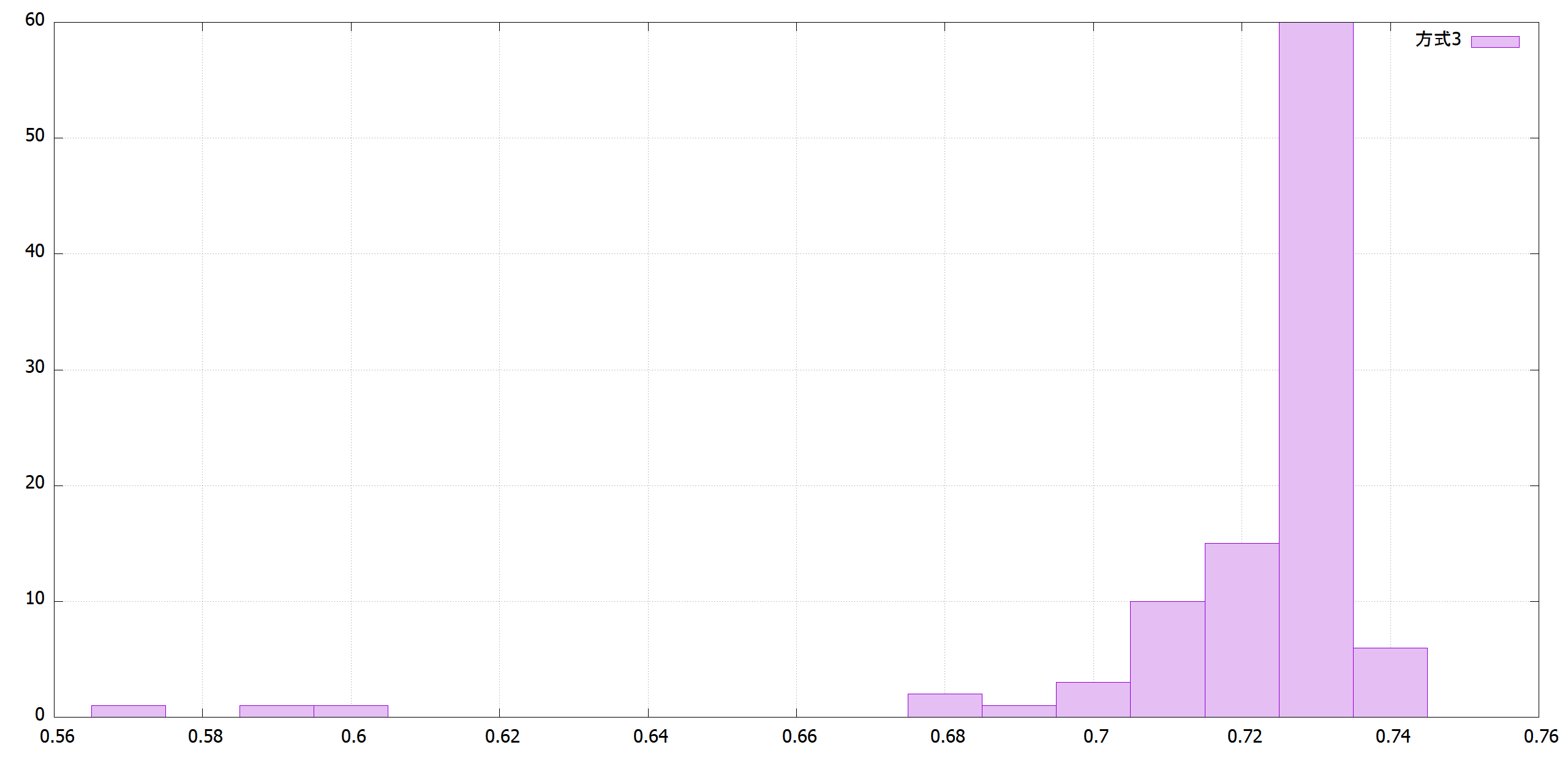
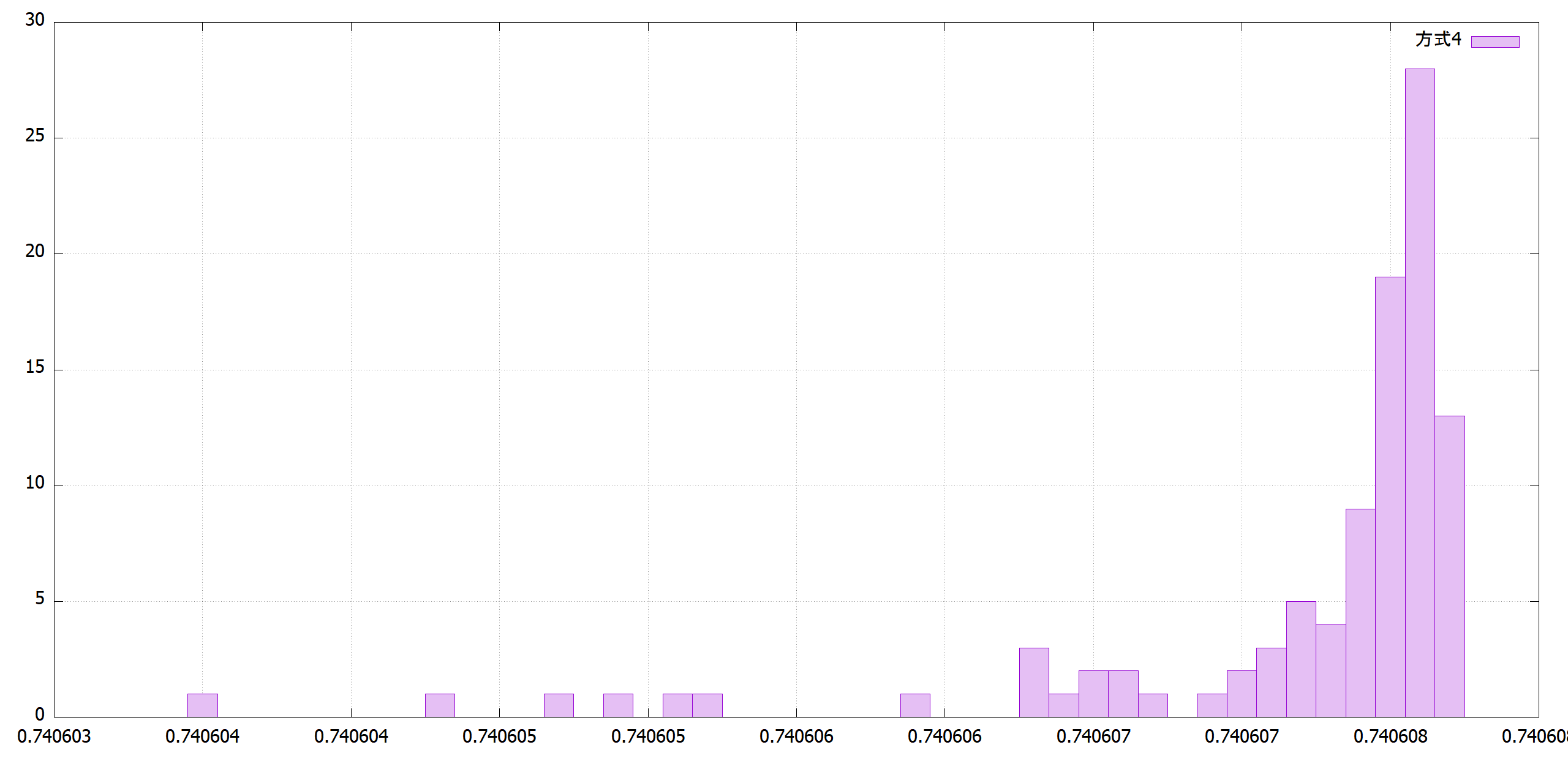
方式1はτが大きすぎて、最後収束していません。方式2のように戦略パラメータを交叉時に平均を取ると3桁合い、方式4のようにτを1/sqrt(2*パラメータ数)にすると5桁合います。
|方式1|方式2|
|-----|-----|----|
| |
| |
|
|方式3|方式4|
| |
| |
|
|方式5|方式6|
| |
| |
|
|方式7||
| ||
||
結論
ボストン住宅価格データセットおよび線形回帰での結論です。
- 交叉は効果あります。
- 戦略パラメータはパラメータ毎に用意すると良いです。
- 交叉時に、戦略パラメータは採用したパラメータの方の戦略パラメータを採用すると良いです。
- 戦略パラメータの変化の度合いを表すτは 1 / sqrt(2 * パラメータ数) が良いです。
- 選択時に親を残すプラス選択の方が良いです。