More than 5 years have passed since last update.

はじパタ9章で飛ばされがちな部分の説明1(グラム-シュミットの正規直交化, 主成分分析)

Last updated at 2017-08-20Posted at 2017-08-13

はじパタ9章をそこそこ頑張って読んでもわからなかった人を対象にしています。
(社内勉強会用なので、言葉足らずな部分があるかも。。コメントしていただけたらできるだけすぐ返事します)
行列の四則演算、転置行列の定義や展開方法、行列の微分、逆行列は知っている前提です。

特異値分解、CLAFIC法に関する説明はこちら↓
http://qiita.com/yukimt3/items/1738bff16046a3d7c501

行列の四則演算、転置行列の定義や展開方法、行列の微分、逆行列に詳しくない人へ

部分空間とは

例題ではじめる部分空間法の11 - 13枚目

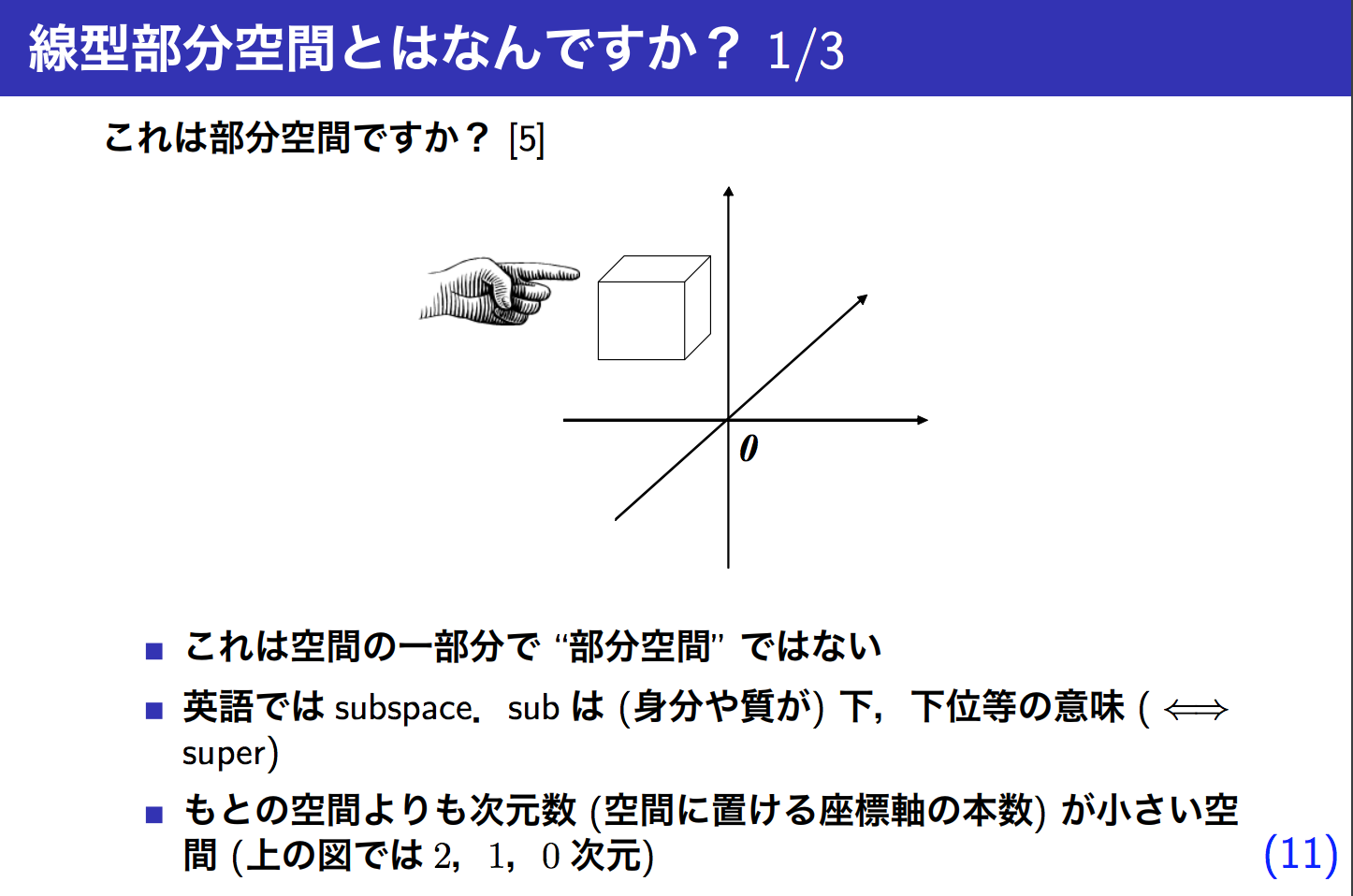
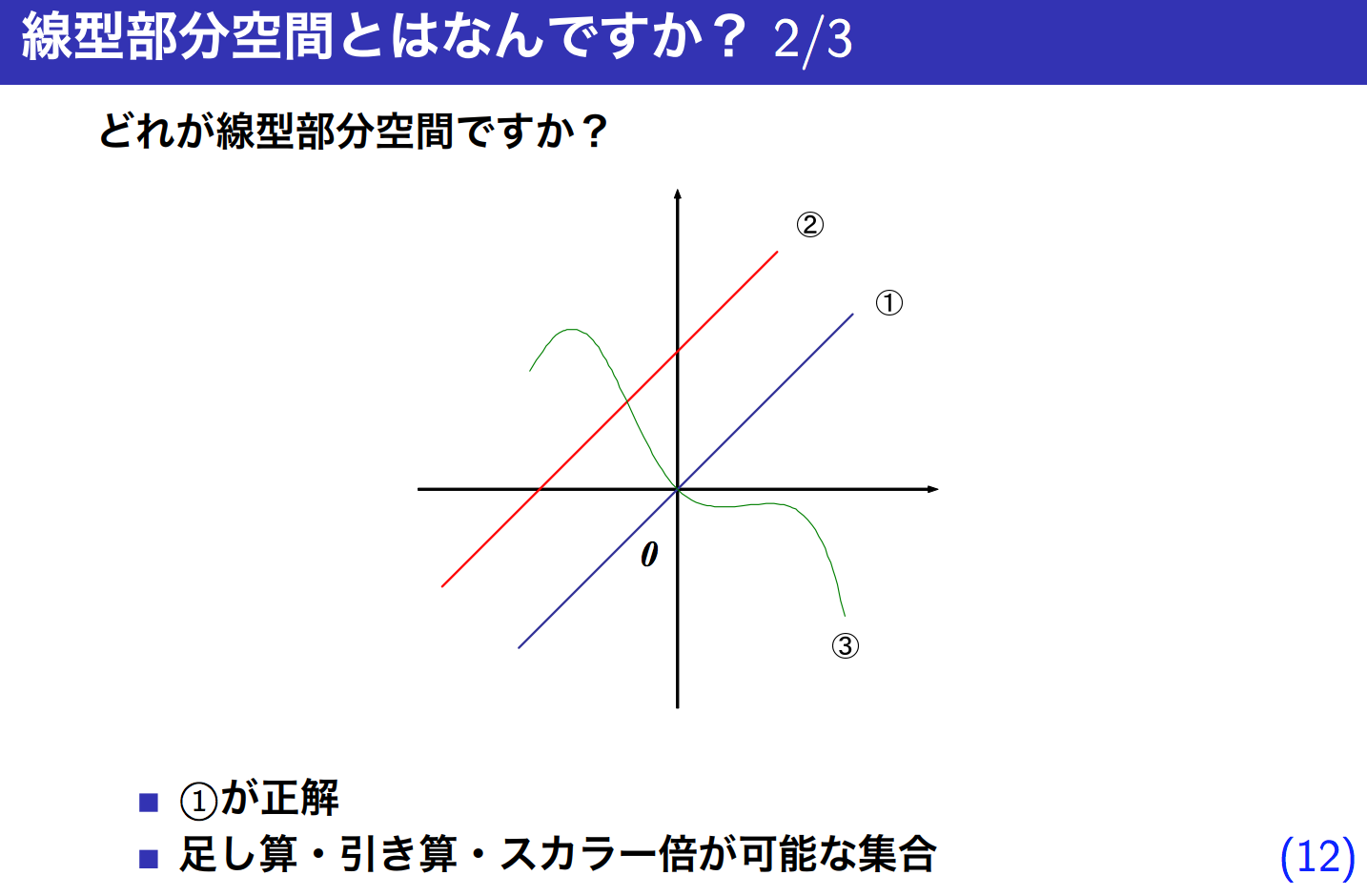
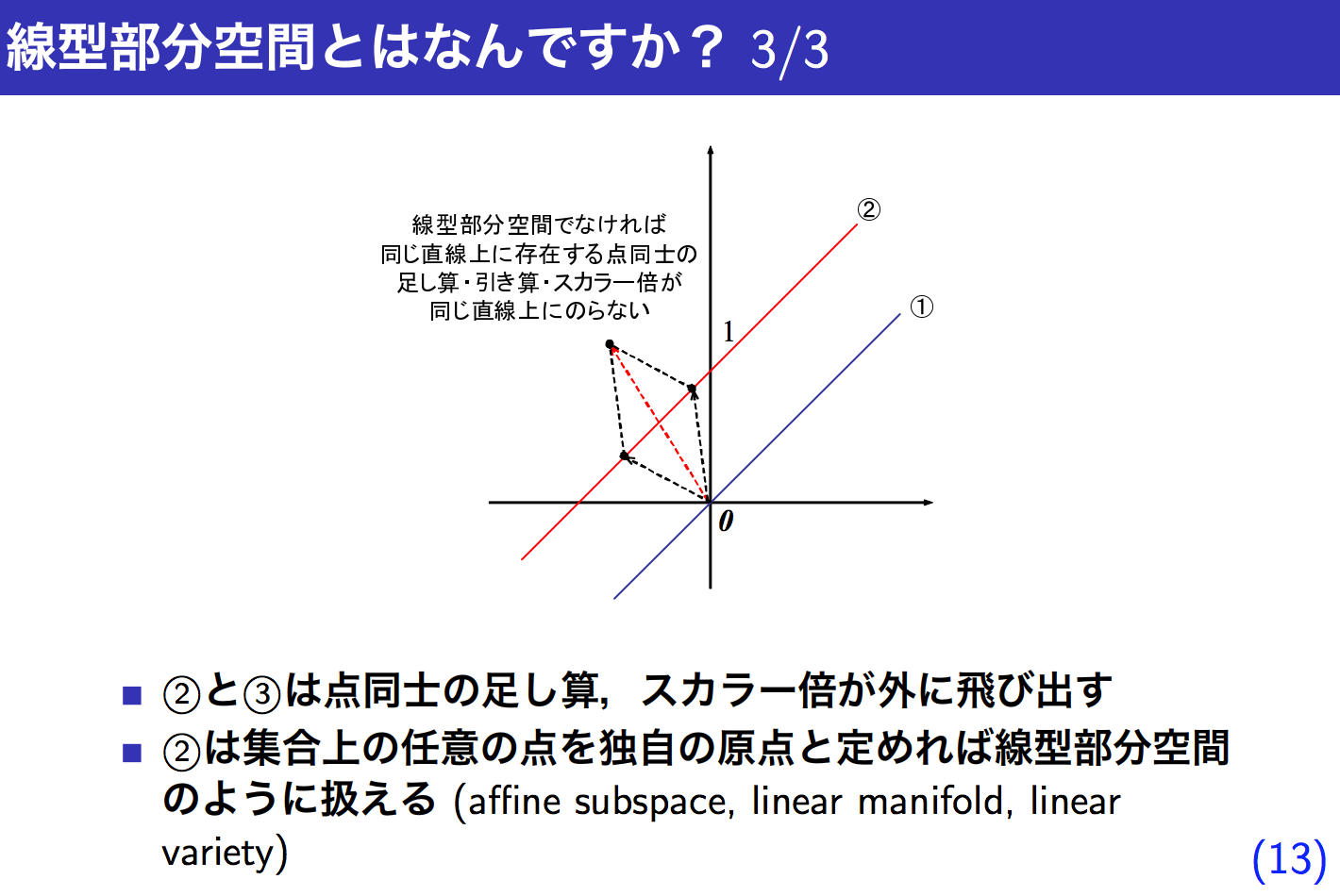
例えばxyzの3次元空間(V)において、xy平面(W)

\vec{x_1} = (1,0,0)\\
\vec{x_2} = (0,1,0)\\

W = \{a_1\vec{x_1} + a_2\vec{x_2} | a_iは実数, i = 1 \cdots 2\}

はxyz空間の部分集合である。
x1の他の要素(この場合はx2だけ)をいくら足したり掛けたりしてもx1は作れない(x2に対しても同様のことが言える)ので、x1, x2 は 一次独立していると言える。

グラム-シュミットの正規直交化

今ある部分空間の基底(x1, x2, ...)から正規直交基底(各ベクトルが直交していて長さが1のベクトルの集合)を導く方法。
例えばxy平面で

\vec{x_1} = (1,0,0)\\
\vec{x_2} = (2,1,0)\\

W = \{a_1\vec{x_1} + a_2\vec{x_2} | a_iは実数, i = 1 \cdots 2\}

だとしても、x1, x2 は一次独立しているし、部分空間としての定義には沿っているがx1とx2は直交してない。
上のx1とx2から新しい基底

\vec{n_1} = (1,0,0)\\
\vec{n_2} = (0,1,0)\\

W = \{a_1\vec{n_1} + a_2\vec{n_2} | a_iは実数, i = 1 \cdots 2\}

を算出しよう！というのがグラム-シュミットの正規直交化になる。

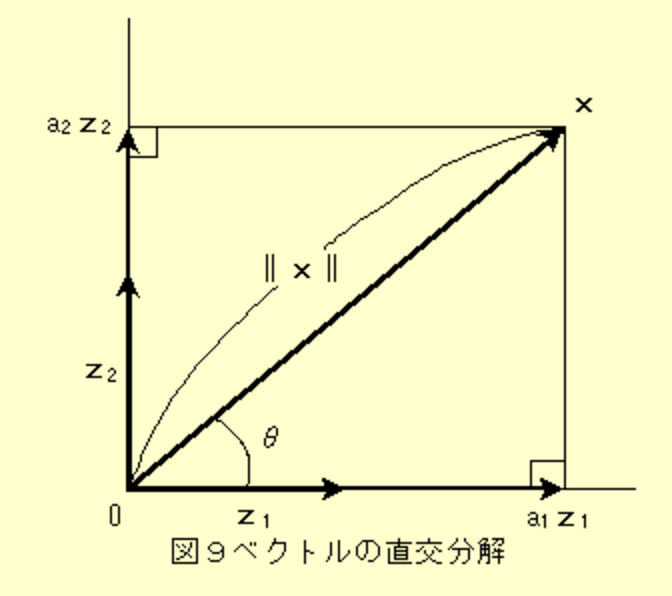http://www.snap-tck.com/room04/c01/matrix/matrix06.html から抜粋

手順

1.x1の単位ベクトルをn1(=上の図で言うz1)とする。
(単位ベクトル := 長さが1のベクトル。)
(||x1||はx1の長さを表しているので、それで割ると n1の長さは1になる)

\vec{n_1} = \vec{x_1} / ||\vec{x_1}||

2.x2(=上の図で言うx)からn1(=上の図で言うz1)方向の成分を除いたベクトル(=> n1と直交するベクトル)の単位ベクトルをn2(=上の図で言うz2)とする。

\vec{n_1}^T\vec{x_2} := \vec{x_2}のn1方向の長さ(スカラー値。上の図で言うa_1)\\
(\vec{n_1}^T\vec{x_2})\vec{n_1} := \vec{x_2}のn1方向の成分(ベクトル。上の図で言うa_1\vec{z_1})\\
\vec{\tilde{n_2}} = \vec{x_2} - (\vec{n_1}^T\vec{x_2})\vec{n_1}　:= 上の図で言うa_2\vec{z_2}\\

\vec{n_2} = \vec{\tilde{n_2}} / ||\vec{\tilde{n_2}}|| := 上の図で言う\vec{z_2}

これでn1, n2 が求まった。
3次元以上の場合は
「x3からn1, n2方向の成分を取り除いた単位ベクトルを求めてn3とする」
「x4からn1, n2, n3方向の成分を取り除いた単位ベクトルを求めてn4とする」
...
としていく。

主成分分析

概要とビジネスへの応用例: http://bdm.change-jp.com/?p=2761

情報量をあんまり削減せずに次元数を削減+データを無相関化できるので、
次元の呪いを軽減する効果や、重回帰分析の精度向上(重回帰分析で説明変数同士が相関関係にあるとうまくいきづらいので)が期待できます。

主成分分析に関する解説はネットにいっぱいあるので、ここでははじパタ9章を読んでて自分が「ん？」って思った部分だけピックアップします。

用語解説

共分散行列
共分散
ラグランジュの未定乗数法(ある制約のもと、関数f(x,y)の値が最大になるようなx,yを求める方法)
固有値、固有ベクトル
実対称行列: (aij = ajiになる行列。ざっくりいうと斜めにバーっと線引いてこっち側と向こう側が同じようになっている)

なぜ「主成分分析 = 学習データの分散が最大になる方向への線形変換」なのか

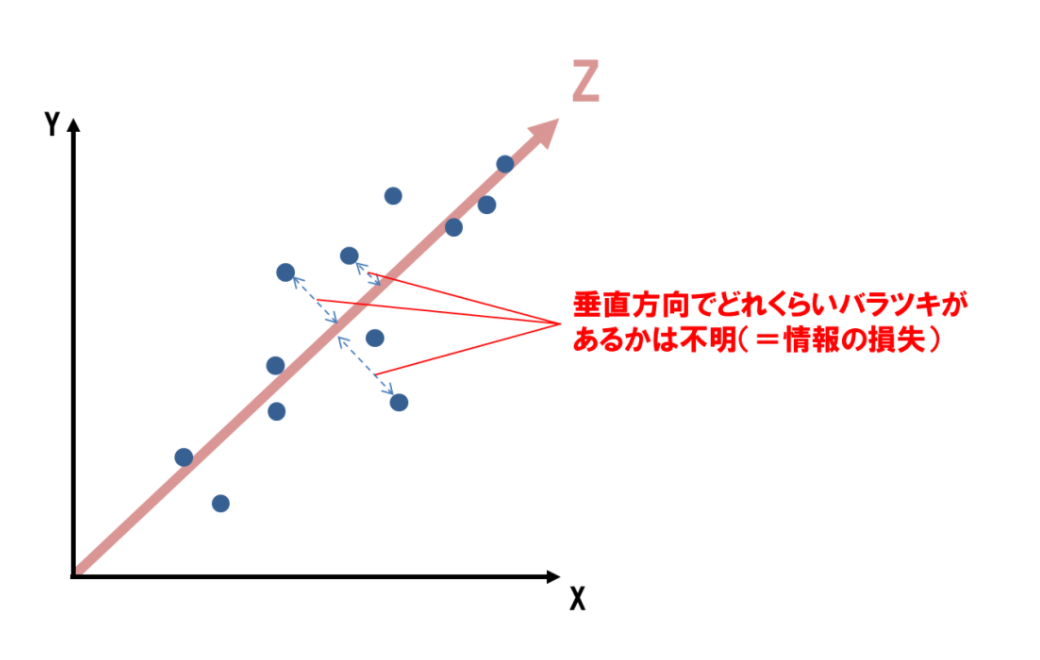
http://bdm.change-jp.com/?p=2761
より抜粋

上の図のように分散が大きい方向(Z方向)を新しい軸にしたほうが情報の損失が一番少なくなる(=次元削減しながらも情報量を担保する)から。

そもそも「学習データの分散が最大になる方向への線形変換」とは

難しい言い方をしたので具体例を下に示す。
(上の図の Z が今回求めたい「学習データの分散が最大になる方向」となる)

Zを頑張って計算(計算方法はもっとあとで説明)した結果

\vec{Z} = \left(
    \begin{array}{ccc}
      1/\sqrt{2},1/\sqrt{2}
    \end{array}
  \right)^T\\
\vec{x_1} = \left(
    \begin{array}{ccc}
      20, 5
    \end{array}
  \right)^T\\

(x1 : 1番目の学習データ)
となった時、主成分分析後の学習データx1は

\vec{x_1}^T\vec{Z} = \left(\begin{array}{ccc}20,5\end{array}\right)
\left(\begin{array}{ccc}1/\sqrt{2}\\1/\sqrt{2}\end{array}\right) = (25/\sqrt{2})

となる。(第一主成分だけで考えたので線形変換後は1次元データになる)
こんな感じでZ(複数あり得る)で学習データを線形変換すると主成分が抽出できる(=情報量をできるだけ失わずに次元数をさげる)よ、というのが主成分分析。

なぜ「学習データの分散が最大になる方向への線形変換 = データの無相関化」なのか

1.はじパタではなぜいつのまにか sj (ここではsとする)の分散について語っているのか

X = \left(
    \begin{array}{ccc}
      \vec{x_1}, \vec{x_2}, \cdots, \vec{x_N}
    \end{array}
  \right)^T\\
\vec{\overline{x}} := \vec{x_1}, \vec{x_2}, \cdots, \vec{x_N} の平均ベクトル\\
\overline{X} = \left(
    \begin{array}{ccc}
      \vec{x_1} - \vec{\overline{x}}, \vec{x_2} - \vec{\overline{x}} , \cdots, \vec{x_N} - \vec{\overline{x}} 
    \end{array}
  \right)^T\\
\vec{a} = \left(
    \begin{array}{ccc}
      a_1,  a_2, \cdots,  a_d
    \end{array}
  \right)^T\\

\vec{s} = \overline{X}\vec{a}

(x1, x2, ... xN: 学習データ)
としたとき、

主成分分析をする
=> 学習データXの分散が最大になる方向への線形変換
=> Xa(=学習データXをaで線形変換したときのデータ)の分散が最大になるようなaをもとめて、そのaで学習データを線形変換させる
=>X¯a(= s) の分散が最大になるようなaをもとめて、そのaで学習データを線形変換させる
(X¯はXを平均ベクトル分だけ平行移動させた(分布そのままで全体を中央にずらした)だけなので、X¯aの分散が最大になったときはXaの分散も最大になる)

というわけでsの分散が最大になるようなaをもとめて(複数解得られる)、それで学習データを線形変換させると主成分分析ができる！
(ただし、主成分の基底ベクトルの長さは1にしたほうが計算しやすいので(?)
||a|| = 1 という制限を設ける)

###2.sの分散を最大にするaを求める方法

2-1.sの各成分の平均が0になる、ということの証明

\vec{s} = \overline{X}\vec{a}\\
=  \left(
    \begin{array}{ccc}
      x_{11} - \overline{x}_1,x_{12} - \overline{x}_2,\cdots,x_{1d} - \overline{x}_d\\
      x_{21} - \overline{x}_1,x_{22} - \overline{x}_2,\cdots,x_{2d} - \overline{x}_d\\
      \cdots\\
      x_{N1} - \overline{x}_1,x_{N2} - \overline{x}_2,\cdots,x_{Nd} - \overline{x}_d
    \end{array}
  \right)
  \left(
    \begin{array}{ccc}
      a_1\\a_2\\\cdots\\a_d
    \end{array}
  \right)\\
= \left(
    \begin{array}{ccc}
      a_1(x_{11} - \overline{x}_1) + a_2(x_{12} - \overline{x}_2,) + \cdots + a_d(x_{1d} - \overline{x}_d)\\
      a_1(x_{21} - \overline{x}_1) + a_2(x_{22} - \overline{x}_2,) + \cdots + a_d(x_{2d} - \overline{x}_d)\\
      \cdots\\
      a_1(x_{N1} - \overline{x}_1) + a_2(x_{N2} - \overline{x}_2,) + \cdots + a_d(x_{Nd} - \overline{x}_d)
    \end{array}
  \right)

となるので、各成分の平均は

\overline{s} = \frac{a_1(x_{11} - \overline{x}_1) + a_2(x_{12} - \overline{x}_2,) + \cdots + a_d(x_{1d} - \overline{x}_d)\\
+ a_1(x_{21} - \overline{x}_1) + a_2(x_{22} - \overline{x}_2,) + \cdots + a_d(x_{2d} - \overline{x}_d)\\
+ \cdots\\
+ a_1(x_{N1} - \overline{x}_1) + a_2(x_{N2} - \overline{x}_2,) + \cdots + a_d(x_{Nd} - \overline{x}_d)}{N}\\
= \frac{a_1\sum^{N}_{i=1}(x_{i1} - \overline{x}_1) + a_2\sum^{N}_{i=1}(x_{i2} - \overline{x}_2) + \cdots + a_d\sum^{N}_{i=1}(x_{id} - \overline{x}_d)}{N}

各ｊ(1 <= j <= d)において

「平均」の定義により

\overline{x}_j = \frac{\sum^{N}_{i=1}x_{ij}}{N}

よって

\sum^{N}_{i=1}(x_{ij} - \overline{x}_j)
= \sum^{N}_{i=1}(x_{ij})  - N\overline{x}_j\\
= \sum^{N}_{i=1}(x_{ij})  - N\frac{\sum^{N}_{i=1}x_{ij}}{N}\\
= \sum^{N}_{i=1}(x_{ij})  - \sum^{N}_{i=1}x_{ij}\\
= 0

となるので、各成分の平均は

\frac{a_1\sum^{N}_{i=1}(x_{i1} - \overline{x}_1) + a_2\sum^{N}_{i=1}(x_{i2} - \overline{x}_2) + \cdots + a_d\sum^{N}_{i=1}(x_{id} - \overline{x}_d)}{N}\\
= \frac{a_1 \times 0 + a_2\times 0 + \cdots + a_d\times 0}{N}\\
= 0

2-2.sの分散を求める。

2-1と同じ方法でX¯の平均が0であることが証明できるのでX¯の分散Var{X¯}は
「分散」の定義により

Var\{\overline{X}\} = \frac{\sum^{N}_{i=1}(\vec{\overline{x_i}} - 0)^2}{N}\\
= \frac{\sum^{N}_{i=1}\vec{\overline{x_i}}^2}{N}\\
= \frac{\overline{X}^T\overline{X}}{N}

(2行名から3行目は行列の積を計算してみると証明できる)

sの分散を Var{s} とすると
「分散」の定義と上の結果により

Var\{s\} = \frac{\sum^{N}_{i=1}(s_{i} - \overline{s})^2}{N}\\
= \frac{\sum^{N}_{i=1}(s_{i} - 0)^2}{N}\\
= \frac{\sum^{N}_{i=1}s_{i}^2}{N}\\
= \frac{\vec{s}^T\vec{s}}{N}\\
= \frac{(\overline{X}\vec{a})^T(\overline{X}\vec{a})}{N}\\
= \frac{\vec{a}^T\overline{X}^T\overline{X}\vec{a}}{N}\\
= \vec{a}^TVar\{\overline{X}\}\vec{a}

2-3.sの分散が最大になるaを求める。

||a|| = 1 という制限(上で述べたやつ)のもと、　Var{s}　を最大化するaを求める方法は、ラグランジュの未定乗数法の定義とはじパタ138ページ目の上の方の式を読めばそんなに難しくないのでここでは過程は割愛。

ともかく、ラグランジュの未定乗数法によるとsの分散が最大になるaは

Var\{s\}\vec{a} = λ\vec{a}

を満たすので、固有値問題を解いて得られるaで線形変換をする(=データの無相関化)ことで、主成分分析ができる

(ちなみに138ページに出てくる「実対称行列の固有ベクトルは相互に直交する」の証明はこの解説が分かりやすかったです)

参考にしたサイト

非常に分かりやすかったです。本当にありがとうございました。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up