線形代数に固有値という概念が出てきます。最初はイメージしにくいのでは、と思うのですが重要な概念かつ、統計学でも頻繁に利用されるので、これもこの可視化シリーズとしてアニメーショングラフを書いて説明することを試みたいと思います。
1.固有値・固有ベクトルとは?##
まず、固有値・固有ベクトルとはなんぞや。数式で表すと下記のことです。
A{\bf x} = \lambda {\bf x}
${\bf x}\neq {\bf 0}$の${\bf x}$で、行列Aをかけると、長さが$\lambda$倍になるような${\bf x}$の事を固有ベクトル, $\lambda$を固有値と言います。
知らない人は???で、これだけではよくわからないですね。
早速、グラフィカルな説明も交えて説明していきたいと思います。
2.行列Aによる線形変換##
固有値・固有ベクトルの説明の前に、行列による線形変換について取り上げます。
例えば、行列$A$を下記のような数値を成分にもつ行列だとします。
A =
\left[
\begin{array}{cc}
2 & 1 \\
-0.5 & -1.5 \\
\end{array}
\right]
この時$Ax$を計算すると
A{\bf x} = \left[
\begin{array}{cc}
2 & 1 \\
-0.5 & -1.5 \\
\end{array}
\right]
\left[
\begin{array}{cc}
x_1 \\
x_2 \\
\end{array}
\right]
=
\left[
\begin{array}{cc}
2x_1 + x_2 \\
-0.5x_1 - 1.5x_2 \\
\end{array}
\right]
と、なります。${\bf x}=(1, 1)$とすると
A{\bf x} = \left[
\begin{array}{cc}
2 & 1 \\
-0.5 & -1.5 \\
\end{array}
\right]
\left[
\begin{array}{cc}
1 \\
1 \\
\end{array}
\right]
=
\left[
\begin{array}{cc}
2 + 1 \\
-0.5 - 1.5 \\
\end{array}
\right]
=
\left[
\begin{array}{cc}
3 \\
-2 \\
\end{array}
\right]
になります。
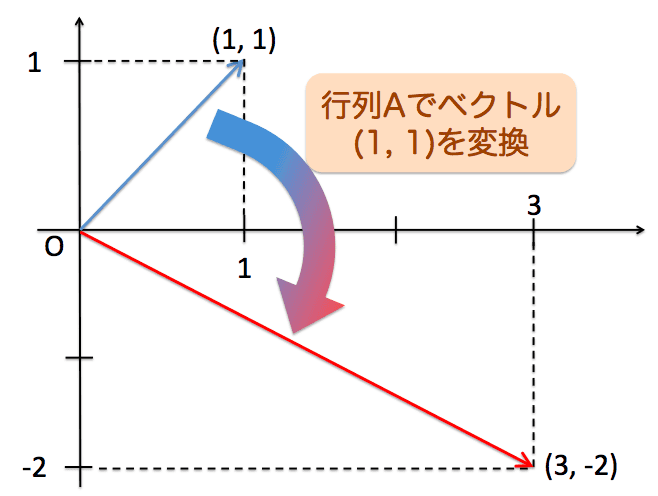
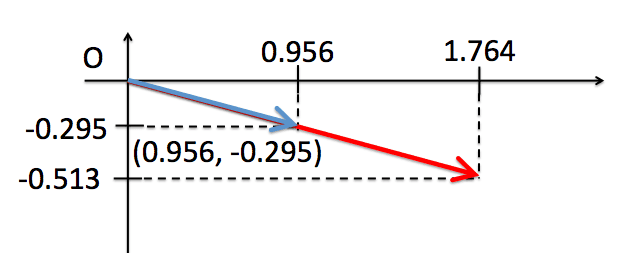
行列$A$を${\bf x}=(1, 1)$にかけると$(3, -2) $になりました。これを図解すると、
という感じで、青いベクトル$(1, 1)$が回転されて、引き伸ばされた感じになっています。なので、この行列をかけるという操作は、**「ベクトルを回転して引き延ばす」**というようにみなすこともできるかと思います。
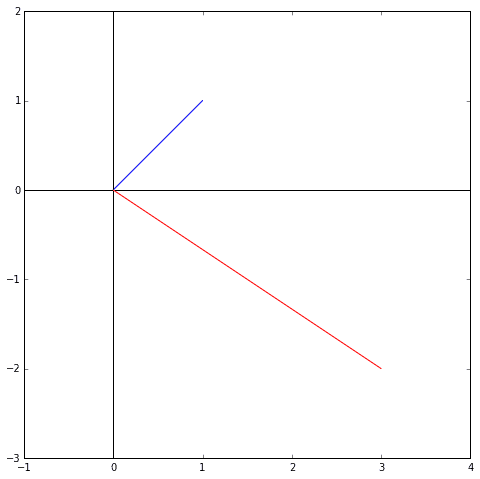
ちゃんと計算してもその通りになるか、Pythonのコードで確認してみます。結果のグラフを見ると、
という感じで、原点から伸びている青い線が (1, 1)ベクトルですが、変換後の赤い線が(3, -2)まで伸びているのがわかります。コードは下記になります。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import animation as ani
plt.figure(figsize=(8,8))
n=20
A = [[ 2, 1],
[-0.5,-1.5]]
x = [1, 1]
a = np.dot(A, x) # ここでAxを計算している
plt.plot([0, x[0]], [0, x[1]], "b", zorder=100)
plt.plot([0, a[0]], [0, a[1]], "r", zorder=100)
plt.plot([-15,50],[0,0],"k", linewidth=1)
plt.plot([0,0],[-40,40],"k", linewidth=1)
plt.xlim(-1,4)
plt.ylim(-3,2)
plt.show()
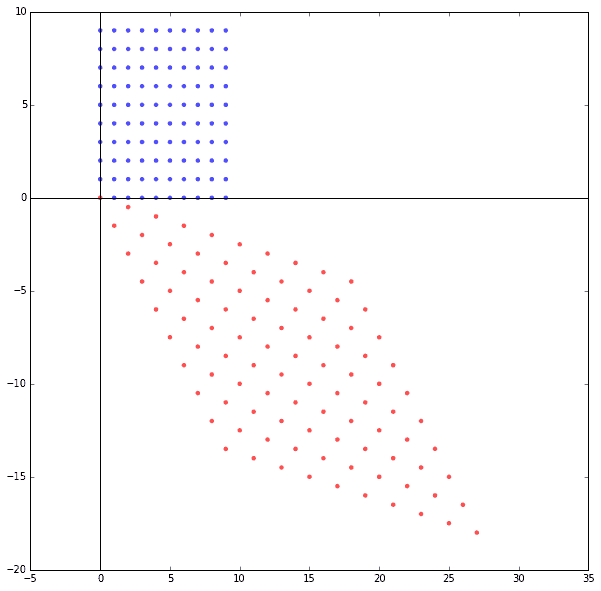
同様に、100個の点を正方形のエリアにプロットして、それを行列$A$で変換をすると平行四辺形に形が変わります。青い正方形の中の各点が、赤い平行四辺形状の点に移っているのです。
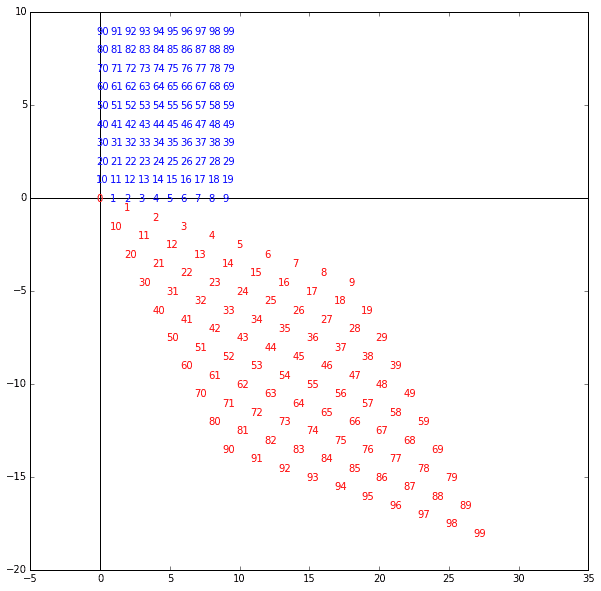
それそれの青い点と赤い点の対応がわかりやすいように、数字でプロットしてみました。
上記のグラフを描くコードはこちらです。
plt.figure(figsize=(10,10))
n=10
xmin = -5
xmax = 35
ymin = -20
ymax = 10
A = [[ 2, 1],
[-0.5,-1.5]]
for i in range(n):
for j in range(n):
x=j
y=i
a = np.dot(A, [x, y])
plt.scatter(x, y, facecolor="b", edgecolors='none', alpha=.7, s=20)
plt.scatter(a[0], a[1], facecolor="r", edgecolors='none', alpha=.7)
plt.plot([xmin,xmax],[0,0],"k", linewidth=1)
plt.plot([0,0],[ymin,ymax],"k", linewidth=1)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.show()
plt.figure(figsize=(10,10))
n=10
xmin = -5
xmax = 35
ymin = -20
ymax = 10
A = [[ 2, 1],
[-0.5,-1.5]]
for i in range(n):
for j in range(n):
x=j
y=i
a = np.dot(A, [x, y])
loc_adjust = .2 # 表示位置の調整
plt.text(x-loc_adjust, y-loc_adjust, "%d"%(i*n + j), color="blue")
plt.text(a[0]-loc_adjust, a[1]-loc_adjust, "%d"%(i*n + j), color="red")
plt.plot([xmin,xmax],[0,0],"k", linewidth=1)
plt.plot([0,0],[ymin,ymax],"k", linewidth=1)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.show()
3.固有値・固有ベクトルの可視化#
前項を踏まえて、固有値・固有ベクトルの式、
A{\bf x} = \lambda {\bf x}
は、下記のグラフのように、行列Aで変換しても、回転せず、単に長さだけが変わるような引き伸ばしのみを行う、Aと${\bf x}$の組み合わせの事になるのです。
これをアニメーションにしてみてみます。
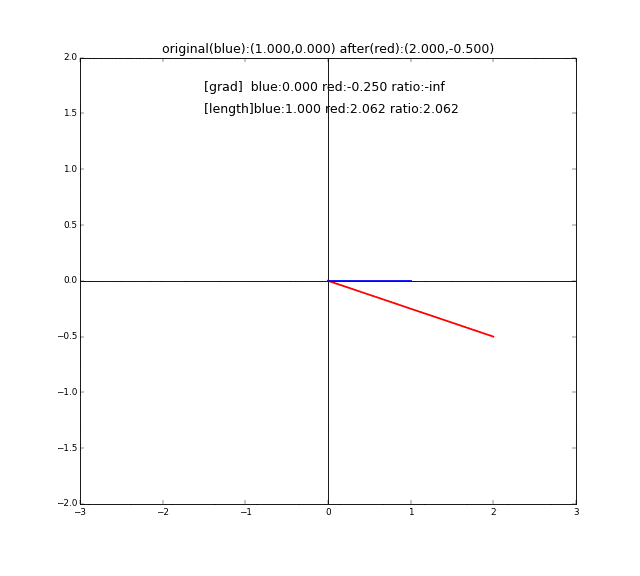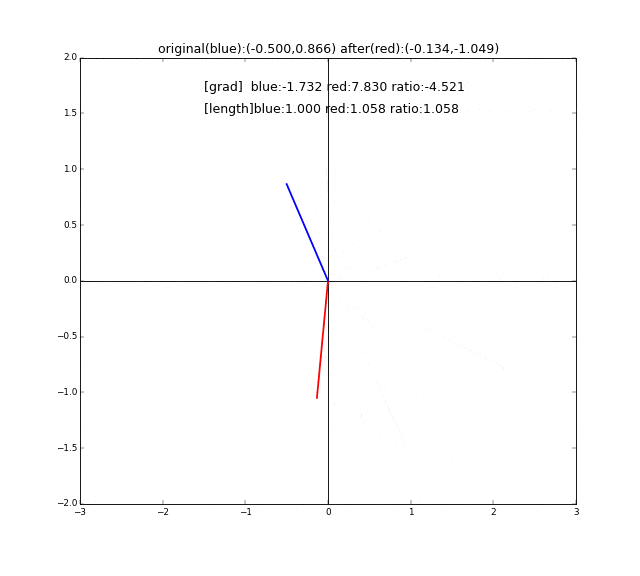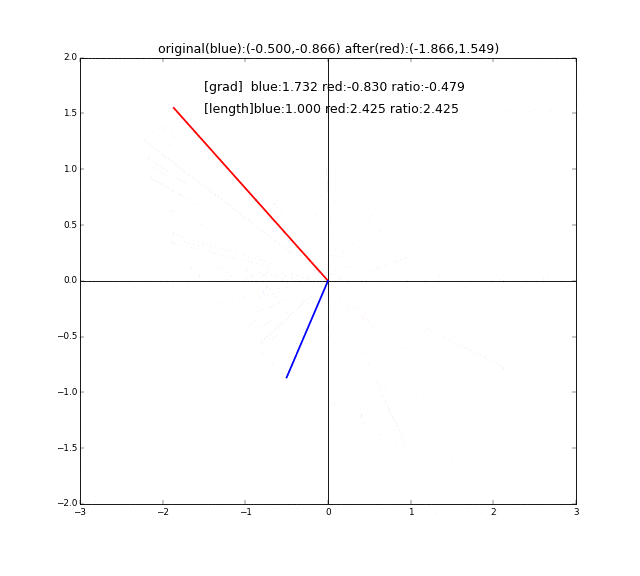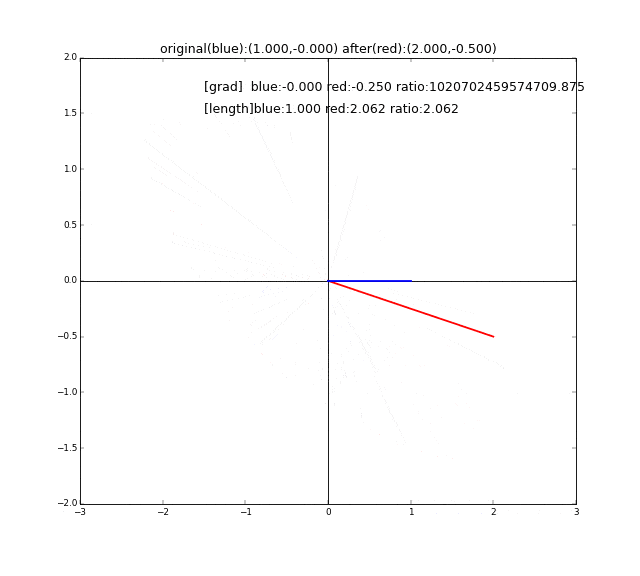
まず変換前のベクトルとして、長さ1のベクトル(青い線)用意して、それをぐるっと360度回転させます。それぞれに対して行列Aで線形変換したベクトル(赤い線)を描画します。この2つの線が一直線上に並ぶ時が、固有値、固有ベクトルに合致するときです。青い線${\bf x}$と赤い線$A{\bf x}$が同じ方向を向いていて長さだけ違う、つまり$A{\bf x}=\lambda {\bf x}$なのです。
わかりやすいように、一直線上に並んでいるときに線が太くなるようしています。
numpyで固有値、固有ベクトルを算出できますのでやってみます。
la, v = np.linalg.eig(A)
print "la",la
print "v",v
結果が下記です。
la [ 1.85078106 -1.35078106]
v [[ 0.98904939 -0.28597431]
[-0.1475849 0.95823729]]
2つの固有値$\lambda_1=1.85078106, \lambda_2=-1.35078106$と、2つの固有ベクトル$x_1=(0.98904939, -0.1475849), x_2=(-0.28597431, 0.95823729)$が得られました。
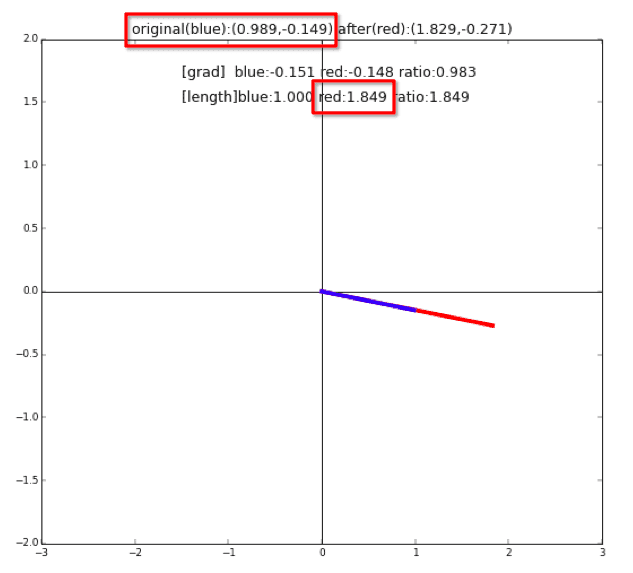
先ほどのアニメーションの一コマを取り出して比較してみましょう。
タイトル部分の"original(blue): (-0.989, -0.149)"は$x_1$とほぼ一致していますね。少し誤差があるのは、アニメーションのフレームレートが荒いためで、もっとレートを上げる(精度を上げる)ともっと一致します。また、"[length] red:1.849"とこれも$\lambda_1$と一致していますね ![]()
なので、固有ベクトルとは、2次元でいうと、原点から360度ぐるっと全方向のベクトルを試してみて、方向が変わらず長さだけが変わる方向のベクトル。固有値とは、その方向のベクトルで変換前と変換後のベクトルの長さの比、ということが言えます ![]()
4.統計学での応用例#
統計学で固有値、固有ベクトルが使われる例を挙げてみたいと思います。
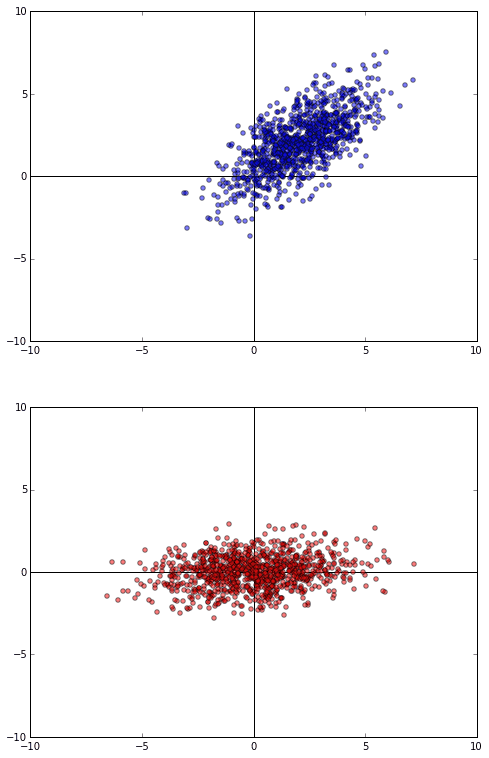
まずちょっとこちらのグラフを見てください。
上の青い点は、2次元正規分布に従う乱数を1000個プロットしたものです。このデータから分散共分散行列を算出すると2x2の行列ができます。この行列の固有ベクトルを算出すると、2次元の固有ベクトルが2つできます。これを2つ並べるとまた行列を作ることができますね。
この固有ベクトルを並べた行列を元データの中心を原点に合わせたものにかけて生成されるデータをプロットしたのが下の赤い点のグラフになります。
データの形を変えずに、回転させて楕円の長い方を水平に持ってきたような変換になっています。
この操作、実は統計学の世界で主成分分析と言われる分析手法になるんです。(主成分分析について書いた記事はこちら)
このように、固有値・固有ベクトルと言う考えは統計学の分野でも用いられています。
この操作を行ったPythonコードが下記になります。
np.random.seed(0)
xmin = -10
xmax = 10
ymin = -10
ymax = 10
# 平均
mu = [2,2]
# 共分散
cov = [[3,2.3],[1.8,3]]
# 2変量正規分布の乱数生成
x, y = np.random.multivariate_normal(mu,cov,1000).T
av_x = np.average(x)
av_y = np.average(y)
# 分散共分散行列をデータより算出
S = np.cov(x, y)
print "S", S
# 固有値、固有ベクトルを算出
la, v = np.linalg.eig(S)
print "la", la
print "v", v
# 原点が中心になるようスライドさせる
x2 = x - av_x
y2 = y - av_y
# 原点をスライドしたデータに、固有ベクトルを並べて作った行列をかける
a1 = np.array([np.dot(v, [x2[i],y2[i]]) for i in range(len(x))])
# グラフの描画
plt.figure(figsize=(8, 13))
# 元データのプロット
plt.subplot(211)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.scatter(x, y, alpha=0.5, zorder=100)
plt.plot([0, 0], [ymin, ymax], "k")
plt.plot([xmin, xmax], [0, 0], "k")
# 固有ベクトルを並べて作った行列をかけたデータのプロット
plt.subplot(212)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.scatter(a1[:,0], a1[:,1], c="r", alpha=0.5, zorder=100)
plt.plot([0, 0], [ymin, ymax], "k")
plt.plot([xmin, xmax], [0, 0], "k")
plt.show()
S [[ 2.6774093 1.93221432]
[ 1.93221432 3.05844013]]
la [ 0.92634075 4.80950869]
v [[-0.74098708 -0.67151928]
[ 0.67151928 -0.74098708]]
vの行列式を計算すると1になっているので、この変換は回転だけを行い、長さは変わっていないことがわかります。
本記事のすべてのPythonコードはこちらにあります。