0. はじめに
最近、強化学習について勉強をはじめました。
かなり難しいですね。
特に、Q学習とSARSAについてoff-policyがどうのとか、on-policyがこうのとか...
とても紛らわしいのでまとめてみました。
参考書として、

を使いました。
強化学習の参考書としては、分かりやすかったのでオススメです。
理解を間違えている点・詳しく説明して欲しい点などございましたら、ぜひ教えてください!
1. 価値反復法とは?
下画像は、【苦しみながら理解する強化学習】第10章 強化学習の特徴軸からお借りしました。
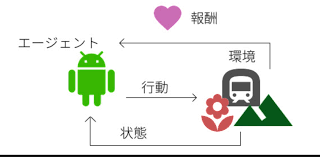
強化学習ではエージェントと環境のやりとりを通して、
「こんな状態だったらこういう行動をとれば、これくらいの報酬がもらえるんじゃないかな?」
といった、価値を推測していきます。(もちろん他にも方法はあります)
価値とは、報酬の総和を推測した値のことです。あくまで、推測値です。
それに対して、報酬はエージェントを環境下で動かすことでしか得られません。
このように、特に、状態と行動の組ごとの価値を関数にしたものを状態行動価値関数とよび、Q(s,a) で表します。基本的には、各状態に対する各行動の価値が書かれた表(Q-table)をイメージして頂ければ問題ありません。
価値反復法とは、この状態行動価値関数(単に価値関数と言ったりもします)をエージェントと環境のやりとりを通して繰り返し更新し、より良くしていきます。
2. 強化学習の流れ
出てくる文字について説明します。
- 状態 s:エージェントのいる状態
- 行動 a:エージェントのとる行動
- 報酬 r:エージェントが環境とのやりとりを通して受け取る報酬
- 方策 π(s,a):エージェントがある状態 s にいる時にある行動 a を選択する確率
- 価値関数 Q(s,a):状態 s で行動 a をとることの価値の関数(前述のとおり)
強化学習の流れは、
- 価値関数 Q、方策 π を初期化する。
- エージェントを送り込む(この時の状態をsとする)
- 方策πと ε-greedy に従ってエージェントの行動 a を決める。
- 状態sにいるエージェントが行動 a をとることで、次の遷移先 s' とそこでの報酬 r' が得られる。
- s, a, s', r'などをもとに価値関数 Q を更新する。
- 価値関数 Q をもとに、価値が最大になるように方策 π を決定する。
- 2.~6.を繰り返す。
といったかんじです。
ε-greedyについては、
ε-greedy行動選択の記事が分かりやすかったです。
行動を選択する際に、ε の確率でランダムに動き、残りの 1-ε の確率は方策 π に従う。
といった考え方です。
3. Q学習とSARSAの違い
ここで、本題の「Q学習とSARSAの違い」についてですが、この違いは上記のステップ5の、
s, a, s', r'などをもとに価値関数 Q を更新する。
という過程にしかありません。
どちらも、あくまではQ関数の更新式なので。
では、詳しい違いをみていきましょう。
価値反復法の更新式
お互いの更新式の違いをみる前に、どちらの場合もざっくりというと、
Q(s_{t},a_{t}) \leftarrow (1-\alpha)Q(s_{t},a_{t}) + \alpha[r_{t+1}+ \gamma Q(s_{t+1},a_{t+1})]
という式になっていることを理解しておいてください。
Qiitaでの数式の書き方が分からなかったので、Qiitaの数式チートシートを参考にさせて頂きました。
- αは学習率というもので、αの割合だけQ値を更新することを意味します。
- γは割引率というもので、時間(ステップ)が進むにつれて、価値がどの程度割り引かれるかを意味します。
また、これを式変形すると、
Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) +
\alpha[r_{t+1}+ \gamma Q(s_{t+1},a_{t+1})-Q(s_{t},a_{t})]
になります。このαで括られた部分の
r_{t+1}+ \gamma Q(s_{t+1},a_{t+1})-Q(s_{t},a_{t})
のことを**TD誤差(Temporal Difference)**と呼びます。
価値反復法ではTD誤差がなるべく小さくなるまで学習を行います。
SARSAの更新式
SARSAというのは、価値関数の更新に、
- 状態 s
- そのときの行動 a
- 遷移先s t+1で得た報酬 r t+1
- 遷移先の状態 s t+1
- 遷移先での行動 a t+1
を用いることからこの名前がつきました。
では、SARSAの更新式をみてみましょう。
Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) +
\alpha[r_{t+1}+ \gamma Q(s_{t+1},a_{t+1})-Q(s_{t},a_{t})]
あれ??
変わってないですね笑
そうなんです!
更新式そのものは変わらないんです。
ここで、大切なのは、
Q(s_{t+1},a_{t+1})
の部分について、ステップ t+1 以降はエージェントを動かしているわけではないので、
ステップt+1における行動はこのままでは未知であるということです。
なので、この部分は何らかの仮定を置いて見積もらないと(計算しないと)いけません。
このt+1での行動をどうやって見積もるかというのが、SARSAとQ学習の違いを生みます。
SARSAでは、この部分を
方策 π とε-greedyに従って動くと仮定して見積もります。
従って、SARSAはon-policy(方策オン)型に分類されます。
方策をオンにしておくと、エージェントを動かしていない場所の価値を見積もる際に、ε-greedy によるランダム性が乗ってきます。
つまり、エージェントがランダムに動くことも想定して見積もることになるので、迷路でいうと崖に落ちるなどのリスクを考慮した上で、価値を更新(学習)することになります。
その結果、エージェントは崖から遠回りするような学習をします。
Q学習の更新式
では、Q学習の更新式をみてみましょう。
Q学習の更新式は、
Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) +
\alpha[r_{t+1}+ \gamma max Q(s_{t+1},a_{t+1})-Q(s_{t},a_{t})]
となります。
Q(s_{t+1},a_{t+1})
の部分が、
max Q(s_{t+1},a_{t+1})
に変わってますね。
「maxってどういうこと??」
ってなると思います。
このmaxというのは、
「今持っている価値関数Qにおいて価値が最大になるような行動をとると仮定して見積もる。」
ということを意味しています。
ですので、価値関数を更新する際は方策は用いません。
従って、Q学習はoff-policy(方策オフ)型に分類されます。
方策をオフにしておくと、エージェントを動かしていない場所の価値を見積もる際に、ε-greedy によるランダム性は乗りません。
つまり、エージェントがランダムに動くことを想定せずに見積もることになるので、迷路でいうと崖に落ちるなどのリスクを考慮せずに、価値を更新(学習)することになります。
その結果、エージェントは崖際でも構わずに進むような学習をします。
4. まとめ
これまでの話をまとめると、
- Q学習とSARSAは価値関数の更新式のみが異なる。
- 価値関数の更新式における、**エージェントを動かしていない場所の価値の見積もり方 Q(st+1, at+1)**が異なる。
- SARSAでは、方策πとε-greedyに従って動くと仮定して見積もる。(on-policy)
- Q学習では、価値が最大になる行動をとると仮定して見積もる。(off-policy)
となります。
質問・修正・記事ネタなど募集してます!