はじめに
今回は以下の記事の続きです。
本プログラムは飛行機をQ-learningにより自動で操縦することを目指したプログラムです。
飛行のモデリングは『航空機力学入門 (加藤寛一郎・大屋昭男・柄沢研治 著 東京大学出版会)』の3章「微小擾乱の運動方程式」をベースに作成しています。
そしてQ-lerningの実装は東京大学松尾研究室の「サマースクール2024 深層強化学習」をベースにしております。
Q学習について理解済みを想定しているため、詳しい説明はほかのサイトをご利用ください。
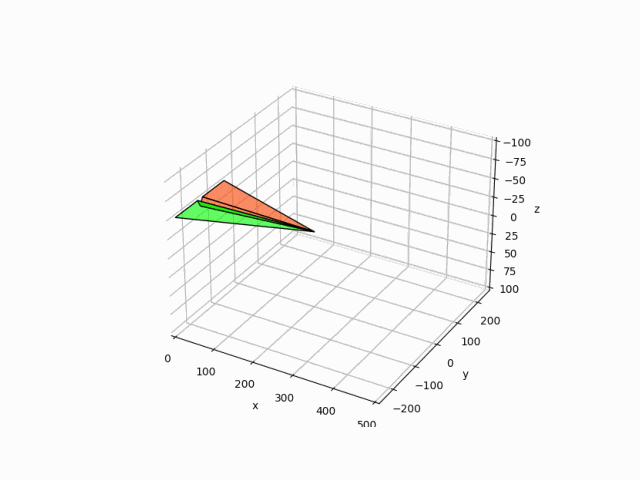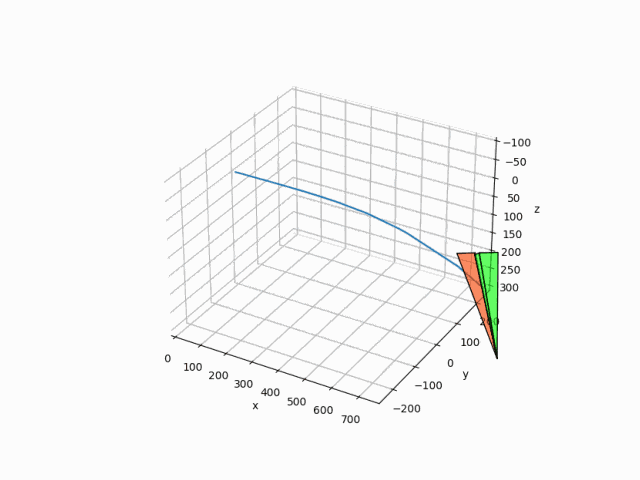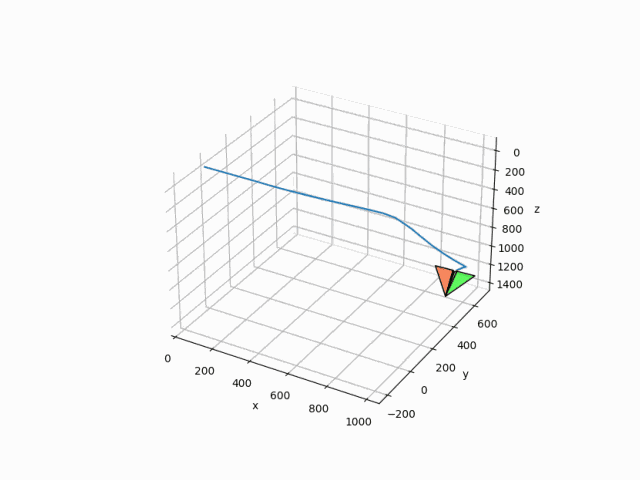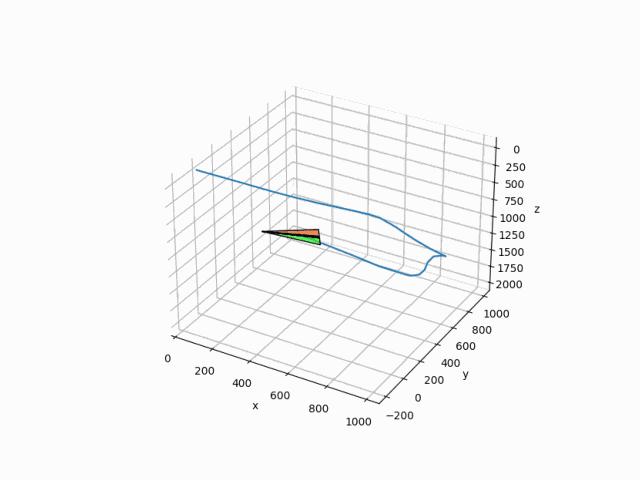
水平旋回を目指して学習させた結果が以下の感じです。
プログラムはgooglecolabで実行できるように公開しています。
各関数
基本的に前回と変わっておりませんが、機体の速度ベクトルを計算する部分を関数化しました。
import numpy as np
from scipy.integrate import odeint, solve_ivp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import time
import mpl_toolkits.mplot3d.art3d as art3d
from IPython.display import HTML
import matplotlib.animation as animation
from tqdm.notebook import tqdm
# --- 回転行列の定義 ---
def rotation_matrix(psi, theta, phi):
# z軸周り回転
R_z = np.array([[np.cos(psi), -np.sin(psi), 0],
[np.sin(psi), np.cos(psi), 0],
[0, 0, 1]])
# y軸周り回転
R_y = np.array([[np.cos(theta), 0, np.sin(theta)],
[0, 1, 0],
[-np.sin(theta), 0, np.cos(theta)]])
# x軸周り回転
R_x = np.array([[1, 0, 0],
[0, np.cos(phi), -np.sin(phi)],
[0, np.sin(phi), np.cos(phi)]])
# 全体の回転行列
R = R_z @ R_y @ R_x
return R
#全体座標系における速度ベクトルの取得
def get_global_velosity(U0, u, alpha, beta, psi, theta, phi):
# 機体座標系での速度ベクトル
u_b = U0 + u
v_b = u_b * np.sin(beta)
w_b = u_b * np.tan(alpha)
vel_b = np.array([u_b, v_b, w_b])
# 全体座標系での速度ベクトル
vel_e = rotation_matrix(psi, theta, phi) @ np.atleast_2d(vel_b).T
vel_e = vel_e.flatten()
return vel_e
#紙飛行機の描写関数
def plot_paper_airplane(x, y, z, phi, theta, psi, scale, ax):
"""
3次元座標と角度が与えられたとき、その状態の紙飛行機のような図形をプロットする
Args:
x: x座標
y: y座標
z: z座標
psi: ロール角 (ラジアン)
theta : ピッチ角 (ラジアン)
phi: ヨー角 (ラジアン)
機体の大きさをいじりたければscaleを変える
"""
#三角形を描く
poly_left_wing = scale * np.array([[2, 0.0, 0],
[-1, 1, 0],
[-1, 0.1, 0]])
poly_right_wing = poly_left_wing.copy()
poly_right_wing[:,1] = -1 * poly_right_wing[:,1]
poly_left_body = scale * np.array([[2, 0.0, 0.0],
[-1, 0.0, +0.1],
[-1, 0.1, 0.0]])
poly_right_body = poly_left_body.copy()
poly_right_body[:,1] = -1 * poly_right_body[:,1]
R = rotation_matrix(psi, theta, phi) # yaw, pitch, roll
for points in [poly_left_wing, poly_left_body, ]:
# 紙飛行機の点を回転
translated_rotated_points = (R @ points.T).T + np.array([x, y, z])
#描写
ax.add_collection3d(art3d.Poly3DCollection([translated_rotated_points],facecolors='orangered', linewidths=1, edgecolors='k', alpha=0.6))
for points in [poly_right_wing, poly_right_body]:
# 紙飛行機の点を回転
translated_rotated_points = (R @ points.T).T + np.array([x, y, z])
#描写
ax.add_collection3d(art3d.Poly3DCollection([translated_rotated_points],facecolors='lime', linewidths=1, edgecolors='k', alpha=0.6))
OpenAIのgym形式での飛行モデルの作成
強化学習ではOpenAIが作成したライブラリであるgymと互換性があるように環境をモデル化することで、過去に作られた豊富な強化学習プログラムがそのまま使えるようになります。
そのため、今回は今まで作成したシミュレーターをgym形式に変更するところから始めていきます。
参考:
飛行モデル
飛行モデルを決める機体パラメータはクラス変数として定義しました。
さらに、飛行をシミュレートする微分方程式はクラス内部で実行できるよう引数に機体速度であるU0を追加しています。
init
initで重要な点としては、ここで時間幅dtを決めていることです。
dtが短ければ細かい入力ができますが、1エピソードの実行時間が長くなります。
逆に大きくしすぎると学習は早くなりますが、かくかくした入力になってしまいます。
また、シミュレーション時間は一律100sにするために、max_episode_stepsを計算しています。これはもともと互換性を持たせるためにenv.spec.max_episode_stepsとアクセスできるようにしたかったのですが、できなかったためenv.max_episode_stepsというようにアクセスするようにしています。
reset
ここでは単に変数を初期化しているだけです。
作成時のバグとして、ここでself.done=False歳忘れていたため、次のステップに移る際にTrueのままなので1ステップでエピソードが終了してしまうという問題がありました。
step
シミュレーション
ここでは、行動であるactionを受け取って1ステップだけ微分方程式を解いています。
ここでactionは入力のベクトルではなく、入力uのどれを選択したかという番号となっています。
そのため、入力uのうちactioonで選択された変数だけ1とし、残りは0とするようなコードにしています。
さらに、プラスかマイナスどちらかわかるように、前半はプラスの入力、後半は間ナスの入力として割り当て、引き算することでu_inpに変換しています。
observation
微分方程式を解いた結果のほか、全体座標系における速度ベクトルも追加して環境observationとしています。
reward
報酬を決める部分で学習でとても重要な部分です。
今回は、水平に180°旋回することを目指しています。
そのため、
- なるべく早く終わってほしいので時間経過で減少
- 目標である真後ろを向いてほしいのでコサイン類似度に応じて増加
- 高度を変えずに旋回してほしいので高度変化に応じて減少
としており、上記はステップごとに行われるため、dtに依存することを避けるためにdtを掛け算して同じ時間当たりの報酬の変化を一定にしています。
さらに、終了判定として
- コサイン類似度が0.95以上 → 報酬を与え終了
- 飛行時間が100sを超える → 終了
というようにしました。
render
今回は今まで作ってきた紙飛行機を描写するプログラムを使い、各フレームの描写をnumpyのarray形式で出力しています。
これによって後から動画を作ることができます。
import gym
class FlightSimulatorEnv(gym.Env):
metadata = {'render.modes': ['rgb_array']}
# --- 機体パラメータ ---
g = 9.81
# 初期条件
U0 = 293.8
W0 = 0
theta0 = 0.0
# 縦の有次元安定微係数: ロッキードP2V-7
Xu = -0.0215
Zu = -0.227
Mu = 0
Xa = 14.7
Za = -236
Ma = -3.78
Madot = -0.28
Xq = 0
Zq = -5.76
Mq = -0.992
X_deltat = 0.01#0
Z_deltae = -12.9
Z_deltat = 0
M_deltae = -2.48
M_deltat = 0
# 横・方向の有次元安定微係数: ロッキードP2V-7
Yb=-45.4
Lb=-1.71
Nb=0.986
Yp=0.716
Lp=-0.962
Np=-0.0632
Yr=2.66
Lr=0.271
Nr=-0.215
#Y_deltaa=0
L_deltaa=1.72
N_deltaa=-0.0436
Y_deltar=9.17
L_deltar=0.244
N_deltar=-0.666
# --- 縦の運動方程式 ---
# 行列A, Bの定義
A_long = np.array([[Xu, Xa, -W0, -g * np.cos(theta0)],
[Zu / U0, Za / U0, 1 + Zq / U0, (g / U0) * np.sin(theta0)],
[Mu + Madot * (Zu / U0), Ma + Madot * (Za / U0), Mq + Madot * (1 + Zq / U0),
(Madot * g / U0) * np.sin(theta0)],
[0, 0, 1, 0]])
B_long = np.array([[0, X_deltat],
[Z_deltae / U0, Z_deltat / U0],
[M_deltae + Madot * (Z_deltae / U0), M_deltat + Madot * (Z_deltat / U0)],
[0, 0]])
# --- 横・方向の運動方程式 ---
# 行列A, Bの定義
A_lat = np.array([[Yb / U0, (W0 + Yp) / U0, (Yr / U0 - 1), g * np.cos(theta0) / U0, 0],
[Lb, Lp, Lr, 0, 0],
[Nb, Np, Nr, 0, 0],
[0, 1, np.tan(theta0), 0, 0],
[0, 0, 1 / np.cos(theta0), 0, 0]])
B_lat = np.array([[0, Y_deltar / U0],
[L_deltaa, L_deltar],
[N_deltaa, N_deltar],
[0, 0],
[0, 0]])
# --- 統合モデル ---
def aircraft_dynamics(self, t, x, U0, A_long, B_long, A_lat, B_lat, u_long, u_lat):
# 縦の運動方程式
dxdt_long = A_long @ np.atleast_2d(x[:4]).T + B_long @ np.atleast_2d(u_long).T
dxdt_long = dxdt_long.flatten()
# 横・方向の運動方程式
dxdt_lat = A_lat @ np.atleast_2d(x[4:9]).T + B_lat @ np.atleast_2d(u_lat).T
dxdt_lat = dxdt_lat.flatten()
# 機体座標系から全体座標系での速度ベクトルへの変換
vel_e = get_global_velosity(U0=U0, u=x[0], alpha=x[1], beta=x[4], psi=x[8], theta=x[3], phi=x[7])
# 縦と横・方向の状態量の変化と位置の変化を結合
dxdt = np.concatenate((dxdt_long, dxdt_lat, vel_e))
return dxdt
def __init__(self):
self.x0 = np.zeros(12)
self.dt = 1
self.max_episode_steps = int(100/1)
self.action_space = gym.spaces.Discrete(8)
self.observation_space = gym.spaces.Box(low=-np.inf, high=np.inf, shape=(15,), dtype=np.float32)
self.reward_range = (-np.inf, np.inf)
self.reset()
def reset(self):
self.x = self.x0
self.t = 0
self.observation = np.concatenate((self.x, np.array([self.U0, 0, 0])))#速度の変数を追加
self.done = False
self.all_soly = self.x0.reshape(len(self.x0),1)
return self.observation
def step(self, action):
start_time = time.time()
u_action = np.zeros(self.action_space.n)
u_action[action] = 1
#u_actionの前半をプラス方向の入力、後半をマイナスの入力として実装
u_inp = u_action[:self.action_space.n//2] - u_action[self.action_space.n//2:]
self.u_long = u_inp[:2]
self.u_lat = u_inp[2:]
# t~t+dtまで微分方程式を解く (RK45メソッドを使用)
sol = solve_ivp(self.aircraft_dynamics, [self.t, self.t+self.dt], self.x,
args=(self.U0, self.A_long, self.B_long, self.A_lat, self.B_lat, self.u_long, self.u_lat),
method='RK45')
#t~t+dtまでの結果を追加
self.all_soly = np.append(self.all_soly, sol.y, axis=1)
#次のt+dtにおける初期条件
self.x = sol.y[:, -1] #現在の最終状態
self.t += self.dt
vel_e = get_global_velosity(U0=self.U0, u=self.x[0], alpha=self.x[1], beta=self.x[4], psi=self.x[8], theta=self.x[3], phi=self.x[7])
#状態量
self.observation = np.concatenate((self.x, vel_e)) * 10
# --- 報酬の設定 ---
# --- 時間に応じた報酬の設定 ---
#短時間で達成できるようにしたい
self.reward = -1 #時間に応じて減額
#高度を変えないでほしい 1000ftで0.1の減少
self.reward -= abs(self.x[11])/10**4
#180°旋回することを目的とする
target_vecor = np.array([-1, 0, 0])
#速度ベクトルと目標ベクトルのコサイン類似度で報酬
vel_e = get_global_velosity(U0=self.U0, u=self.x[0], alpha=self.x[1], beta=self.x[4], psi=self.x[8], theta=self.x[3], phi=self.x[7])
cosine_similarity = np.dot(target_vecor, vel_e)/(np.sqrt(np.dot(target_vecor, target_vecor))*np.sqrt(np.dot(vel_e, vel_e)))
self.reward += cosine_similarity
#時間幅に依存しないようにしたい
self.reward *= self.dt
#ほぼ目標を向いたら終了
if cosine_similarity > 0.95:
self.done = True
self.reward += 100
#終了判定
if self.t >= 100: #100s経過した場合
self.done = True
#self.reward -= 100
#info
self.info = elapsed_time = time.time() - start_time
#print(self.t, self.done, self.reward)
return self.observation, self.reward, self.done, self.info
def render(self, mode='rgb_array'):
if mode == 'rgb_array':
plt.ion()
fig = plt.figure(dpi=100)
ax = Axes3D(fig)
fig.add_axes(ax)
ax.invert_zaxis()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(0, 500)
ax.set_ylim(-250, 250)
ax.set_zlim(100, -100)
# 軌跡
ax.plot(self.all_soly[9], self.all_soly[10], self.all_soly[11])
ax.set_xlim(min(min(self.all_soly[9]),0), max(max(self.all_soly[9]), 500),)
ax.set_ylim(min(min(self.all_soly[10]),-250), max(max(self.all_soly[10]), 250),)
ax.set_zlim(max(max(self.all_soly[11]), 100),min(min(self.all_soly[11]),-100))
#紙飛行機
plot_paper_airplane(x=self.x[9], y=self.x[10], z=self.x[11], phi=self.x[7], theta=self.x[3], psi=self.x[8], scale=100, ax=ax)
# 描画をキャンバスに保存
fig.canvas.draw()
# キャンバスからRGBデータを取得
image = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)
image = image.reshape(fig.canvas.get_width_height()[::-1] + (3,))
#メモリ開放
plt.clf()
plt.close()
return image
def close(self):
pass
def seed(self, seed=None):
pass
Q-learning
Q-learningでは、状態と行動が離散値でないという欠点があります。
そのため、連続値を離散値に変更しています。
参考
- 東京大学松尾研究室の「サマースクール2024 深層強化学習」
- https://qiita.com/sugulu_Ogawa_ISID/items/bc7c70e6658f204f85f9
def bins(clip_min, clip_max, num):
return np.linspace(clip_min, clip_max, num+1)[1:-1]
# 状態を離散化して対応するインデックスを返す関数(binの上限・下限はcartpole環境固有のものを用いています)
def discretize_state(observation, num_discretize):
u, alpha, q, theta, beta, p, r, phi, psi, x, y, z, ug, vg, wg = observation
discretized = [
np.digitize(u, bins=bins(-20, 20, num_discretize)),
np.digitize(alpha, bins=bins(-1, 1, num_discretize)),
np.digitize(q, bins=bins(-2, 2, num_discretize)),
np.digitize(theta%(2*3.14), bins=bins(0, 2*3.14, num_discretize)),
np.digitize(beta, bins=bins(-1, 1, num_discretize)),
np.digitize(p, bins=bins(-2.0, 2.0, num_discretize)),
np.digitize(r, bins=bins(-2.0, 2.0, num_discretize)),
np.digitize(phi%(2*3.14), bins=bins(0, 2*3.14, num_discretize)),
np.digitize(psi%(2*3.14), bins=bins(0, 2*3.14, num_discretize)),
np.digitize(x, bins=bins(-2*10**5, +2*10**5, num_discretize)),
np.digitize(y, bins=bins(-2*10**5, +2*10**5, num_discretize)),
np.digitize(z, bins=bins(-2*10**3, +2*10**3, num_discretize)),
np.digitize(ug, bins=bins(-500, +500, num_discretize)),
np.digitize(vg, bins=bins(-500, +500, num_discretize)),
np.digitize(wg, bins=bins(-500, +500, num_discretize)),
]
return sum([x*(num_discretize**i) for i, x in enumerate(discretized)])
class QLearning:
def __init__(self, num_state, num_action, num_discretize, gamma=0.99, alpha=0.5):
self.num_action = num_action
self.gamma = gamma # 割引率
self.alpha = alpha # 学習率
# Qテーブルを作成
self.qtable = np.zeros((num_discretize**num_state, num_action))
# Qテーブルを更新
def update_qtable(self, state, action, reward, next_state):
self.qtable[state, action] = (1 - self.alpha) * self.qtable[state, action] + self.alpha* (reward + self.gamma * self.qtable[next_state].max())
# Q値が最大の行動を選択
def get_greedy_action(self, state):
action = np.argmax(self.qtable[state])
return action
# ε-greedyに行動を選択
def get_action(self, state, episode):
epsilon = 0.7 * (1/(episode+1)) # ここでは0.5から減衰していくようなεを設定
if epsilon <= np.random.uniform(0,1):
action = self.get_greedy_action(state)
else:
action = np.random.choice(self.num_action)
return action
実行結果
Q-learningによって学習された水平旋回を目指した飛行結果が以下になります。
正直後ろは向いてくれたものの高度はかなり落ちてしまいました。
報酬の与え方が悪いのか、それともQ-learingの限界なのかはわかりません。
報酬の与え方をいろいろ試しては見たものの、これが限界でした。
# 各種設定
num_episode =2000#1200 # 学習エピソード数
num_discretize = 5 # 状態空間の分割数
#penalty = 1000#10 # 途中でエピソードが終了したときのペナルティ
# ログ
episode_rewards = []
num_average_epidodes = 10
env = FlightSimulatorEnv()
max_steps = env.max_episode_steps #env.spec.max_episode_steps # エピソードの最大ステップ数
agent = QLearning(env.observation_space.shape[0], env.action_space.n, num_discretize)
for episode in tqdm(range(num_episode)):
observation = env.reset() # envからは4次元の連続値の観測が返ってくる
state = discretize_state(observation, num_discretize) # 観測の離散化(状態のインデックスを取得)
episode_reward = 0
for t in range(max_steps):
action = agent.get_action(state, episode) # 行動を選択
observation, reward, done, _ = env.step(action)
episode_reward += reward
#print(reward, episode_reward)
next_state = discretize_state(observation, num_discretize)
agent.update_qtable(state, action, reward, next_state) # Q値の表を更新
state = next_state
if done:
break
episode_rewards.append(episode_reward)
if episode % 50 == 0:
tqdm.write("Episode %d finished | Episode reward %f" % (episode, episode_reward))
# 累積報酬の移動平均を表示
moving_average = np.convolve(episode_rewards, np.ones(num_average_epidodes)/num_average_epidodes, mode='valid')
plt.plot(np.arange(len(moving_average)),moving_average)
plt.title('Q-Learning: average rewards in %d episodes' % num_average_epidodes)
plt.xlabel('episode')
plt.ylabel('rewards')
plt.show()
env.close()
実行結果
最後に
今回は、Q学習により水平旋回をさせるプログラムを作りました。
シミュレーション環境をgym形式に変更するところから始めるとかなり知識が身につき、学習環境がよくわかりました。
反面、Q学習についての説明は省いてしまったため、そこはもう少しちゃんとやってもよかったなと感じています。
今回は「その3」だったのですが、
その4ではニューラルネットワークを利用したDQNにすることで、連続値を扱えるようにしたいと考えています。