【PyQUBO】SA法を用いて適切なランニングのコースを提案してみた

概要

最近，家でいることが多いので健康のためにランニングを始めたいと思っています．

その際に使う「ランニングの管理アプリ」は，走った距離やタイムを記録しておき，トレーニングプランを自動で提案してくれるものがほとんどです．

このようなアプリを使う中で，運動のために

自宅から特定の地点まであえて遠回りするランニングコース

を提案する仕組みは，需要があるのかはさておき，おそらく存在しないと思い，シミュレーティッド・アニーリング（SA法）の技術を用いた実装をしてみました．

定式化

本記事では，PyQUBOを用いてランニングコースを提案するモデルの定式化を行うことにします．

QUBO

QUBOは制約条件付きの最適化を行うモデルです．$\ x_i={0,1}$の2値をとるバイナリ変数を用いて，目的関数は以下の形をとります．

\begin{align*}
\mathcal{H}(\boldsymbol{x})=\sum_{i<j}x_iQ_{ij}x_j\ 
\end{align*}

二次形式の目的関数を構築すると，行列$\ Q_{ij},$へ落とし込む変換はPyQUBOが自動で行ってくれます．上式をハミルトニアンと呼び，「ハミルトニアンをどのように数式で記述するか」が肝になります．

目的関数

最短経路探索に関する論文を参考に，バイナリ変数$,x_{i,p},$をもつ行列$\ X,$を定義します．

\begin{align}
X=\left[
\begin{array}{cccc}
x_{1,1}&x_{1,2}&\cdots&x_{1,P}\\
x_{2,1}&x_{2,2}&\cdots&x_{2,P}\\
\vdots&\vdots&\ddots&\vdots\\
x_{V,1}&x_{V,2}&\cdots&x_{V,P}
\end{array}
\right]\ 
\end{align}

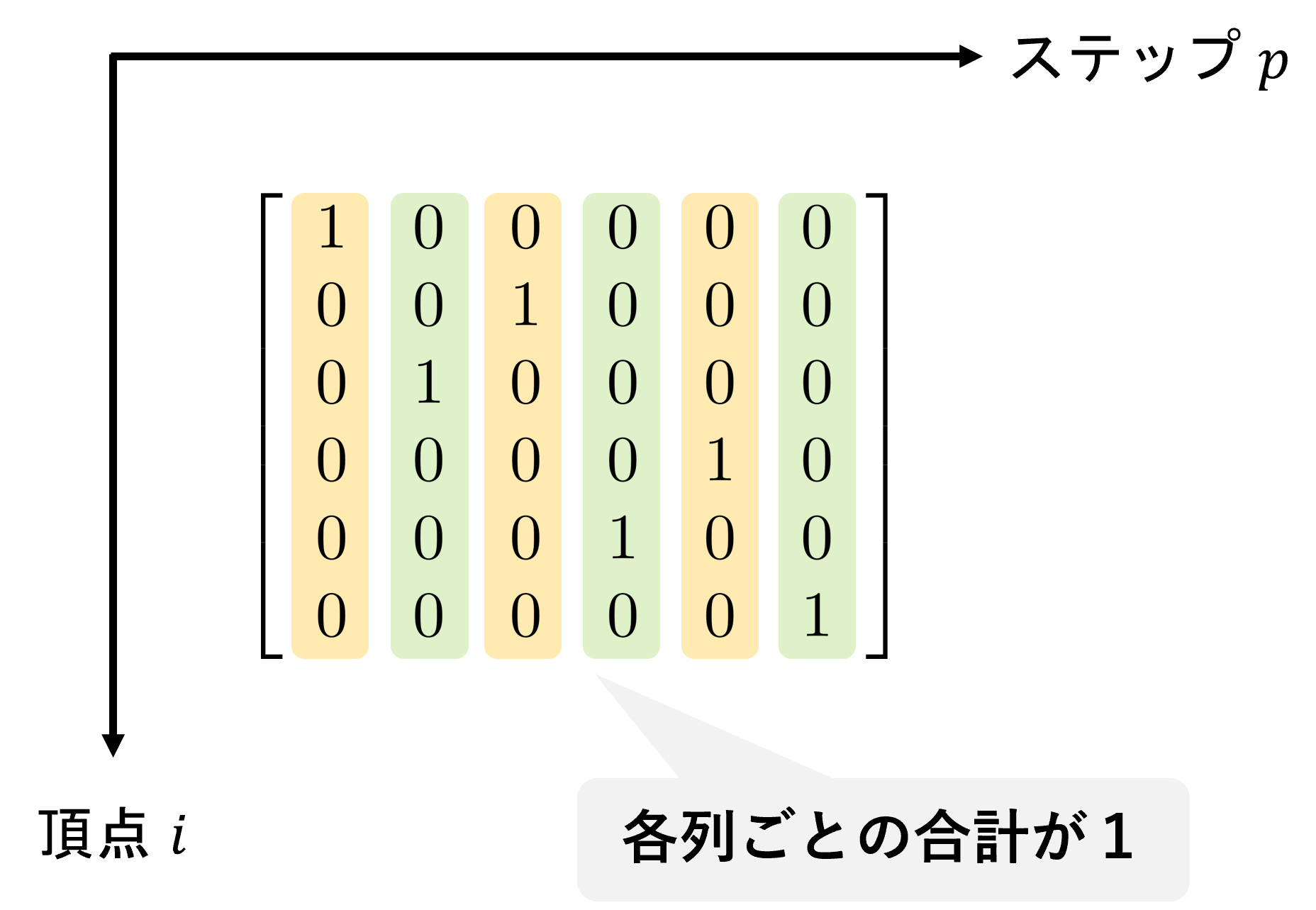
この要素が$,x_{i,p}=1,$の値をとるとき，「頂点$\ i,$を$,p,$番目に通る」ことを意味します．例えば，$\ x_{2,3}=1\ $は頂点2を3番目のステップで通ることを表します．

(※論文中では$\ p,$は position(位置) と呼ばれていますが，本記事では「ステップ」と読み替えています)

具体的に，以下図のような1番から6番までの全部で$,V=6,$個の頂点を持つパスを考えると，

行列$\ X\ $の要素は次のように表現されることになります．

上で定義された行列要素(バイナリ変数)を用いて目的関数を構築すると，次式でハミルトニアンが形成されます．

\begin{align*}
H_C=\sum_{p=1}^{P-1}\sum_{i=1}^V\sum_{j=1}^Vc_{i,j}x_{i,p}x_{j,p+1}
\end{align*}

$\ c_{i,j},$は頂点$, i-j,$間を結ぶ経路の長さです．頂点同士がつながっていない場合は$\ c_{i,j},$を大きな値にセットします．

$,P,$は論文中では“ホップ数”と呼ばれ，スタートからゴールまで何地点経由するかを表すパラメータとなります．

制約条件１

各ステップで，1つの地点のみを通過する条件は以下のように表せます．

\begin{equation*}
H_P=\sum_{p=1}^P\left(1-\sum_{i=1}^Vx_{i,p}\right)^2
\end{equation*}

$,H_P=0,$のとき，$\ X,$のうち各列ごとの要素の合計が１となる条件を満たします．これは言い換えると「各ステップで１頂点のみ通る」という制約にほかなりません．

制約条件２

次に，スタート地点$,s,$とゴール地点$,t,$に関する制約条件です．

\begin{equation*}
H_s=(1-x_{s,1})^2\qquad H_t=(1-x_{t,P})^2
\end{equation*}

$\ H_s,$は最初のステップで頂点$,s,$を通過することを表し，$,H_t,$は最終ステップ$\ P,$のとき，頂点$\ t,$に行きつくことを表します．

制約条件３

最後に「各地点は一度だけ通過する」という条件を式で記述します．

\begin{equation*}
H_V=\sum_{i=1}^V\sum_{1\leq p<q\leq P}x_{i,p}x_{i,q}
\end{equation*}

地点$\ i,$をステップ$\ p,$の時に通過した際は$\ x_{i,p}=1\ $であり，それ以外のステップ$,q,$では$\ x_{i,q}=0\ $となるように式を構築すると上式のように記述されます．

定式化まとめ

これまでに出てきたハミルトニアンを集約して，一つのモデルにします．

\begin{align*}
\mathcal{H}(\boldsymbol{x})=H_C+\alpha\bigl(H_P+H_s+H_t+H_V\bigr)
\end{align*}

各項の制約条件を表にしてまとめると以下のようになります．

式	効 果	役割
$,,H_C,$	距離最小化	目的関数
$,,H_P,$	各ステップで１地点のみ通過	制約条件
$H_s,\ H_t\ $	初期(最終)ステップで地点$,s,(t),$を通る	制約条件
$,,H_V,$	各地点は一度だけ通過	制約条件

実装

実装の際には，主として以下のライブラリを用います．

• pyqubo == v1.0.12
• numpy == v1.21.5
• neal == v0.5.7
• networkx == v2.6.3
• osmnx == v1.1.2
• folium == v0.12.1

osmnxのインストールはこちらの記事を参考にしました．

ディレクトリ構成は以下のようにします．

RouteOptimizerクラス

ルート最適化のためのハミルトニアンを構築するクラスを設定します．関数属性は以下のようにします．

• get_adj：距離行列取得
• construct：ハミルトニアン構築
• decode：ソルバーから返ってきた解をデコードし，グラフ構造として出力

「route_optimizer.py」というファイルに以下のコードを記述します．

route_optimizer.py

import osmnx as ox
import networkx as nx
import numpy as np
from pyqubo import Array, Placeholder, Constraint


class RouteOptimizer:


    def __init__(self, pos:tuple, dist:int = 200, **args):

        G = ox.graph_from_point(pos, network_type = "walk", dist = dist, **args)
        self.graph = nx.convert_node_labels_to_integers(G)
        self.quad_var = None



    def get_adj(self):
        """ get adjacency matrix """

        mat = nx.adjacency_matrix(self.graph, weight = "length").todense()
        arr = np.array(mat).astype(float)
        arr[arr == 0] = arr.sum()
        return arr



    def construct(
        self, source:int, target:int, n_hop:int = 10, shortest:bool = True
        ):
        """ construct hamiltonian """

        # define qubo array
        X = np.array(Array.create("Xout", (len(self.graph), n_hop), "BINARY"))

        # constraints
        Hp = sum((1 - X.sum(axis = 0)) ** 2)
        Hs = np.square(1 - X[source, 0])
        Ht = np.square(1 - X[target, n_hop - 1])
        Hv = sum([X[:, p] @ X[:, q] for q in range(n_hop) for p in range(q)])
        Hconst = Hp + Hs + Ht

        # adjacency matrix
        adj = self.get_adj()

        if shortest:
            adj *= 1 - np.eye(len(self.graph))
        else:
            Hconst += Hv
            msg = "n_hop must be less than or equal to number of nodes"
            if n_hop > len(self.graph): warnings.warn(msg, UserWarning)


        # calculate objective function
        Xtmp = np.delete(X, 0, 1)[:, :n_hop]
        Hobj = np.sum(X[:, :n_hop - 1].dot(Xtmp.T) * adj)

        # compiled hamiltonian
        H = Hobj + Placeholder("alpha") * Constraint(Hconst, "constraint")
        self.quad_var = H.compile()
        self.n_hop = np.size(X, 1)



    def decode(self, solution:dict):
        """ decode sample data & create output graph structure """

        # Output array
        Xout = np.zeros((len(self.graph), self.n_hop))
        for key, val in solution.items(): exec("{}={}".format(key, val))


        # optimized route
        via_nodes = np.argmax(Xout, axis = 0)
        unique_arr, index = np.unique(via_nodes, return_index = True)
        path = unique_arr[index.argsort()]


        # input graph info
        edge = [(*e, 0, self.graph.edges[(*e, 0)]) for e in zip(path, path[1:])]
        node = [(n, self.graph.nodes[n]) for n in path]


        # construct output 'path' graph
        Gout = nx.MultiGraph()
        Gout.add_edges_from(edge)
        Gout.add_nodes_from(node)
        Gout.graph.update(self.graph.graph)


        return Gout

sampling関数

アニーリングを実行する関数を作成します．「solver.py」ファイルに記述します．

• with_info：束縛条件を満たしているかの判定
• feed_dict：束縛条件項の係数$\ \alpha\ $

solver.py

import neal
import numpy as np

def sampling(model, with_info:bool = False, feed_dict:dict = None, **args):

    """ Simulated Annealing """
    feed_dict = feed_dict if feed_dict else {"alpha":np.max(model.get_adj())}
    bqm = model.quad_var.to_bqm(feed_dict = feed_dict)
    response = neal.SimulatedAnnealingSampler().sample(bqm, **args)
    samples = model.quad_var.decode_sampleset(response, feed_dict = feed_dict)
    solution = min(samples, key = lambda x: x.energy)

    if with_info:
        return solution.sample, solution.constraints()
    else:
        return solution.sample

Visualizerクラス

最後に，グラフ構造を可視化するクラスを作成します．「visualizer.py」ファイルにソースを記述します．

• render：地図上に地点・経路の反映
• save：地図情報の保存(html形式)
• add_route：経路情報の追加
• draw：matplotlibを用いて地図描画

visualizer.py

import folium
import osmnx as ox
import networkx as nx
from folium import Circle




class Visualizer:

    def __init__(self, model, **args):


        self.G = model.graph
        self.routes = []
        self.__draw_config = {"bgcolor":"w", "edge_color":"k", "node_color":"k"}
        self.__folium_config = {"weight":2, "tiles":"OpenStreetMap", "fill":False,
                                "fill_color":"k", "fill_opacity":0.1,
                                "radius":1, "color":"blue"}

        self._update_params_(args, self.__folium_config)
        self.fmap = ox.plot_graph_folium(self.G, **self.__folium_config)



    def render(self, **opts):
        """ rendering map """

        self._update_params_(opts, self.__folium_config)
        data = list(self.G.nodes(data = True))
        X = list(map(lambda d: [d[1]["y"], d[1]["x"]], data))

        for n, pos in enumerate(X):
            Circle(pos, popup = n, **self.__folium_config).add_to(self.fmap)



    def save(self, path:str):
        """ save to html file """
        self.fmap.save(outfile = path)



    def add_route(self, route:list, **opts):
        """ add route to `fmap` """
        self.routes.append(route)
        ox.plot_route_folium(self.G, route, route_map = self.fmap, **opts)



    def draw(self, **opts):
        """ show map """
        self._update_params_(opts, self.__draw_config)
        if self.routes:
            ox.plot_graph_routes(self.G, self.routes, **self.__draw_config)
        else:
            ox.plot_graph(self.G, show = True, **self.__draw_config)


    def _update_params_(self, args:dict, origin_params:dict):

        # update parameters
        for key, val in args.items():
            origin_params.update({key:val})

実験

実装セクションで作成したファイル群はすべて「engine」ディレクトリにまとめます．

次に，これらのファイル群を呼び出すメインの「dev_ex.py」ファイルを作成します．以下のように記述します．

dev_ex.py

from engine.route_optimizer import RouteOptimizer
from engine.visualizer import Visualizer
from engine.solver import sampling



pos = (34.3976198, 132.4753631)  # Hiroshima-Station
model = RouteOptimizer(pos, dist = 200)
state = Visualizer(model)
state.render()
state.save("./output_images/output1.html")

model.construct(8, 45, shortest = False, n_hop = 28)
solution, info = sampling(model, num_reads = 1000, with_info = True)
print(info)

if info.get("constraint")[0]:
    path_graph = model.decode(solution)
    route = list(path_graph.nodes)
    state.add_route(route, color = "red")
    state.save("./output_images/output2.html")

グラフ構造全体のプロット

「output1.html」ファイルにグラフ構造の全体像をプロットします．
今回は，広島駅周辺の地図を緯度・経度の座標で指定してピックアップしました．

各地点のところにカーソルをあてるとポップアップが表示されます．表示される番号はグラフ構造の頂点を指定する番号です．

※今回は8番-45番をそれぞれ始点-終点として経路探索を行ってみます．

最短経路

「model.construct()」の引数で「shortest」をTrueにします．
これにより，始点から終点までの最短経路(の近似解)を求めることができます．

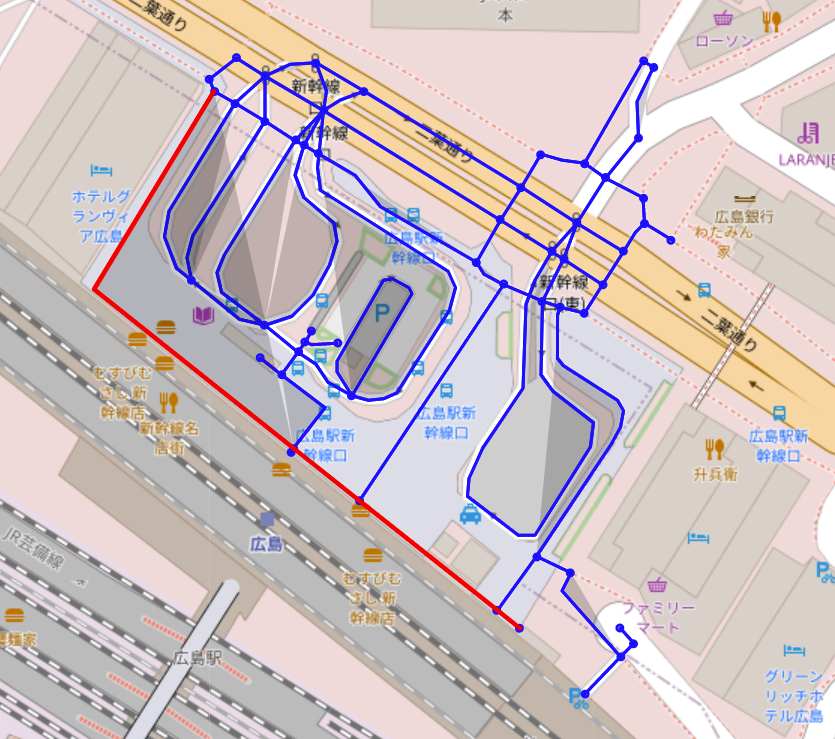
↑経路のプロットは「output2.html」ファイルに保存しています

ランニングコースの提案

「shortest」をFalseにして，「model.construct()」のキーワード引数「n_hop」の値を変更してみます．この引数は

始点から終点まで何地点経由するか

を設定するもので，ハミルトニアンの式中のパラメータ$\ P\ $に対応します．

目的地までより長い距離を走ってたどり着きたい場合は引数「n_hop」の値を増やせばよいわけです．

n_hopをいろいろな値に設定して出力してみました．

• n_hop=12

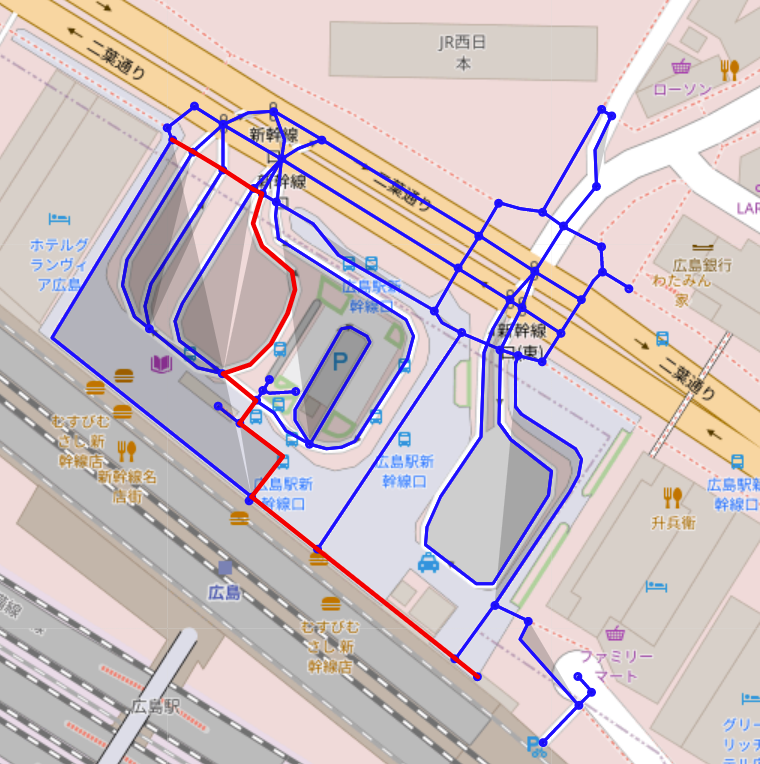
• n_hop=17

• n_hop=28

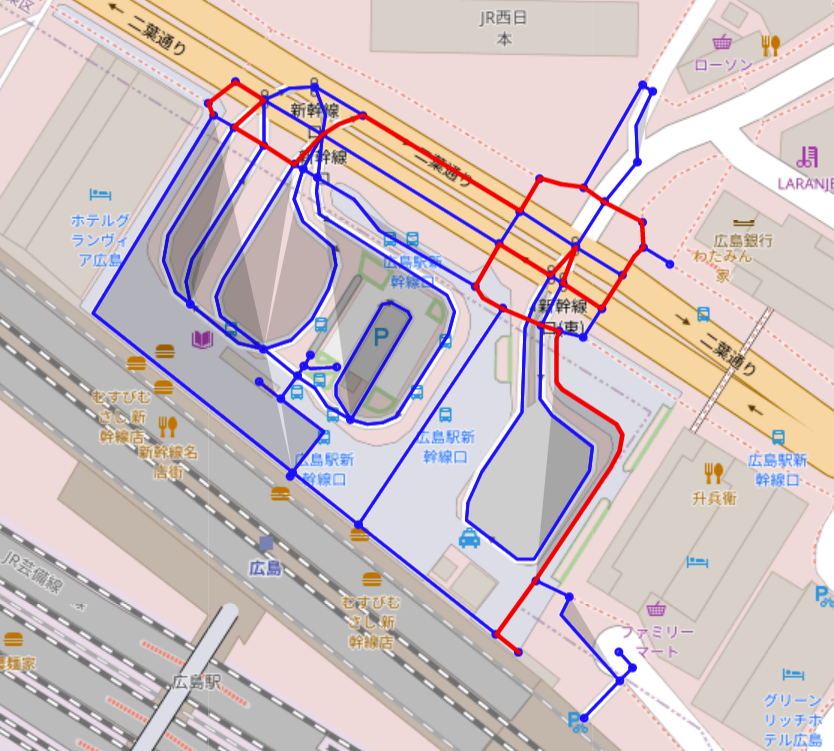
確かにn_hopで指定された数の頂点を経由して，終点までたどり着くことができています！

n_hopは経由する地点数だったので，個人の運動したい量に合わせてこのパラメータを調節すれば色々な経路パターンを提案してくれます！

• 【応用】巡回路を提案する

始点から出発して元の位置に戻ってきたいというユースケースも考えられると思います．

これを達成するには，

1. 始点と近接する位置に終点を置く
2. 始点から終点までn_hop数経由してたどり着く経路を求める
3. 始点-終点を直接結ぶ

の手順を踏めばよいはずです．

今回構築したモジュールを用いて，以下のように実装します．(※dev_ex.pyと同じ階層のディレクトリに作成)

=======================
   ソースコードを表示 (dev_ex1.py)
 ========================

dev_ex1.py

from engine.route_optimizer import RouteOptimizer
from engine.visualizer import Visualizer
from engine.solver import sampling



pos = (34.3976198, 132.4753631)  # Hiroshima-Station
model = RouteOptimizer(pos, dist = 200)
state = Visualizer(model)
state.render()
state.save("./output_images/output1.html")

model.construct(10, 11, shortest = False, n_hop = 22)
state.add_route([10, 11], color = "red", weight = 4)
solution, info = sampling(model, num_reads = 1000, with_info = True)
print(info)

if info.get("constraint")[0]:
    path_graph = model.decode(solution)
    route = list(path_graph.nodes)
    state.add_route(route, color = "red", weight = 4)
    state.save("./output_images/output2.html")

巡回路となるランニングコースもいい感じに提案できています！

まとめ＆参考

本記事では，以下の論文の式を参考にランニングの経路をよしなに提案するモデルを作りました．

• Solving the Network Shortest Path Problem on a Quantum Annealer