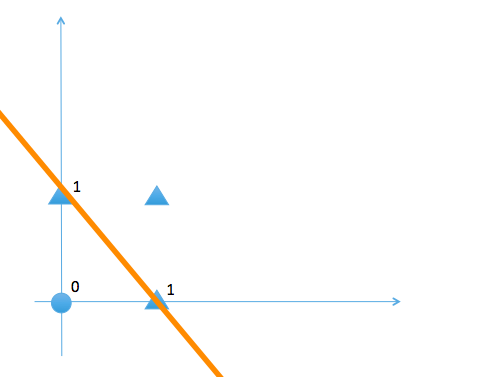この記事はAizu Advent Calendar 2016 8日目の記事です。
前の人は@0xShoneさん、次の人は@masapontoさんです。
パーセプトロンとは、1957年、ローゼンブラットというアメリカの研究者によって考案されたアルゴリズムのことですが、人工知能や機械学習、ディープラーニングなどのアルゴリズムの礎になっており、それらを理解する上では必須知識です。
そんなパーセプトロンを分かりやすく解説していきます。
パーセプトロンとは?
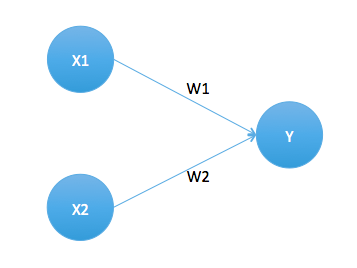
パーセプトロンは、複数の入力に対して1つ出力する関数です。
出力は$1$か$0$の2値です。
それぞれの$x_1$,$x_2$は入力信号、$y$は出力信号、$w_1$,$w_2$は重みを表します。図の◯はニューロンと呼びます。
入力信号$x$に重み$w$が乗算され、その総和が一定のしきい値を超えたら$1$を出力します。それ以外は$0$を出力します。
$1$を出力した場合「ニューロンが発火する」と表現したりします。
式に表すと
\begin{eqnarray}
y=\left\{ \begin{array}{ll}
0 & (\sum_{i=1}^nw_ix_i \leqq \theta) \\
1 & (\sum_{i=1}^nw_ix_i > \theta) \\
\end{array} \right.
\end{eqnarray}
$\theta$はしきい値です。
パーセプトロンは複数ある入力のそれぞれに固有の重みを持っていて、その重みが各信号の重要度を表しています。
パーセプトロンを使ってANDゲートを作ってみる
ANDゲートとは入力$x_1$,$x_2$に対しての出力$y$を満たすものです。
2入力に対して1出力です。
| No | $x_1$ | $x_2$ | $y$ |
|---|---|---|---|
| 1 | $0$ | $0$ | $0$ |
| 2 | $1$ | $0$ | $0$ |
| 3 | $0$ | $1$ | $0$ |
| 4 | $1$ | $1$ | $1$ |
この真理値をみたすように$w_1,w_2,\theta$を決めます。
とりあえず適当に値を当てはめてみて、探っていきます。
$(w_1,w_2,\theta) = (0.5,0.5,0.7)$
の場合
■$x_1=0,x_2=0,y=0$ の場合
$0 × 0.5 + 0 × 0.5 < 0.7$ なため $0$ が出力される。 $y$ と同じ値のためOK
■$x_1=1,x_2=0,y=0$ の場合
$1 × 0.5 + 0 × 0.5 < 0.7$ なため $0$ が出力される。 $y$ と同じ値のためOK
■$x_1=0,x_2=1,y=0$ の場合
$0 × 0.5 + 1 × 0.5 < 0.7$ なため $0$ が出力される。 $y$ と同じ値のためOK
■$x_1=1,x_2=1,y=1$ の場合
$1 × 0.5 + 1 × 0.5 > 0.7$ なため $1$ が出力される。 $y$ と同じ値のためOK
つまり、ANDゲートはパーセプトロンで$(w_1,w_2,\theta) = (0.5,0.5,0.7)$で表せます。
実は解答は一つではなく、$(0.5,0.5,0.8)$ や $(1.0,1.0,1.0)$ でも表すことができます。
このような方法でNANDゲートやORゲートも表す事ができます。
今回パラメータを手探りで値を決めました。このパラメータを決定する作業を自動で行わせることを機械学習と言います。
パーセプトロンの限界
パーセプトロンの登場により、1960年代にニューラルネットワークのブームが起こりました。
しかし、1969年に発表されたマービン・ミンスキーによる研究報告により、パーセプトロンの致命的な欠点が明らかになり、ブームは終焉を迎えてしまいました。
パーセプトロンは線形分離可能な問題なら正しく学習することができましたが、線形分離不可能な問題は、正しく学習できません。
有名な問題として、XORゲート(排他的論理和)が挙げられます。
XORゲートの入力と出力の組み合わせは以下になります。
| No | $x_1$ | $x_2$ | $y$ |
|---|---|---|---|
| 1 | $0$ | $0$ | $0$ |
| 2 | $1$ | $0$ | $1$ |
| 3 | $0$ | $1$ | $1$ |
| 4 | $1$ | $1$ | $0$ |
XORゲートは線形分離不可能なため、$(w_1,w_2,\theta)$の組み合わせを見つける事ができません。
線形分離可能、線形分離不可能とは直線で領域を表現できるか否かです。
ORゲートの場合
このように◯と△を一つの直線で領域を分けることができます。これが線形分離可能といいます。
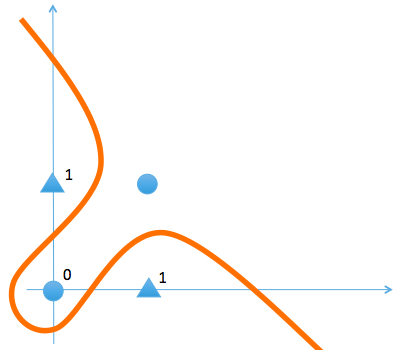
XORゲートの場合
このように◯と△を一つの直線で領域を分けることができず、どうしても曲線になってしまいます。これが線形分離不可能といいます。
多層パーセプトロン
パーセプトロンではXORゲートを表現できませんでしたが、実は層を重ねることによって、XORゲートを表現することができます!
つまり、いくつかのゲートを組み合わせて配線することによってXORゲートを作ってしまうということができるのです。
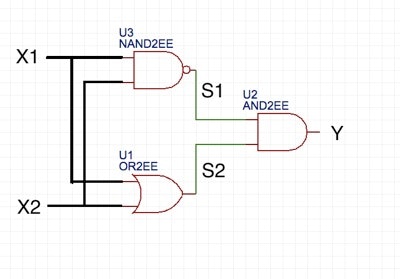
XORゲートを表現するにはいくつかの方法がありますが、今回はAND、NAND、ORを使って、表現してみましょう。
| No | $x_1$ | $x_2$ | $s_1$ | $s_2$ | $y$ |
|---|---|---|---|---|---|
| 1 | $0$ | $0$ | $1$ | $0$ | $0$ |
| 2 | $1$ | $0$ | $1$ | $1$ | $1$ |
| 3 | $0$ | $1$ | $1$ | $1$ | $1$ |
| 4 | $1$ | $1$ | $0$ | $1$ | $0$ |
これでXORゲートを完成させることができました。
層が1層のみのものを単層パーセプトロン、層が複数のものを多層パーセプトロンといいます。
まとめ
実はNANDゲートだけでコンピュータが行っている処理を再現できます。(詳しくはこちら→ コンピュータシステムの理論と実装 )
ですので、パーセプトロンは層を重ねることによってコンピュータのような複雑な処理も表現できるようになる素晴らしいアルゴリズムです。