正規分布のグラフについて

はじめに

春から社内SEとなりました。
諸々勉強中ですので、熟練の方にとっては物足りない内容かもしれません。
Qiitaの投稿内容は私のメモ程度の内容ですので
所属する組織の見解や学術的な内容ではありません。
頑張って更新続けます。

正規分布の確率密度関数とは

平均μ、分散σ^2の正規分布の確率密度関数は下記のように表現されます。

X〜N(\mu,\sigma^2)

ならば

f(x) = \frac{1}{\sqrt{2π\sigma^2}}\times\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)

正規分布のグラフとは

上記の確率密度関数のグラフを書きたいと思います。
グラフを書くには微分して増減表を書きます。
（合成関数の微分です）

\begin{align}
\frac{df(x)}{dx} &= \frac{1}{\sqrt{2π\sigma^2}}\times\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)\times(-\frac{1}{2\sigma^2}\times2\times(x-\mu))\\

&=f(x)\times\frac{-(x-\mu)}{\sigma^2}
・・・①
\end{align}

（まあまあ綺麗にまとまります）
もう一回微分します。
（積の微分です）

\begin{align}
\frac{d}{dx}\frac{df(x)}{dx}&= \frac{df(x)}{dx}\frac{-(x-\mu)}{\sigma^2}+f(x)\frac{-1}{\sigma^2}\\
&= f(x)\times\frac{-(x-\mu)}{\sigma^2}\times\frac{-(x-\mu)}{\sigma^2}-f(x)\frac{1}{\sigma^2}\\
&= f(x)\times\frac{1}{\sigma^4}\times(x-\mu)^2-f(x)\frac{1}{\sigma^2}\\
&= f(x)\frac{1}{\sigma^4}
((x-\mu)^2-\sigma^2)\\
&= f(x)\frac{1}{\sigma^4}
((x-\mu)+\sigma)((x-\mu)-\sigma)
・・・②
\end{align}

（綺麗です）

よって増減表は下記の通りです。

x	・・・	μ	・・・
①	+	0	-
f(x)	・・・	極大	・・・

x	・・・	μ-σ	・・・	μ+σ	・・・
②	+	0	-	0	+
f(x)	・・・	変曲点	・・・	変曲点	・・・

ちなみに

\begin{align}
\lim_{x\rightarrow\pm\infty}\exp(-x^2)=0
\end{align}

であるので

\begin{align}
\lim_{x\rightarrow\pm\infty}f(x)=0
\end{align}

です。
(ここでは厳密な証明を避けております。はさみうちの原理？です。
私の知能を察してください。)

よって平均μ、分散σ^2の正規分布のグラフは
μ（平均値）で極大になり、μから±σ（標準偏差）離れているところで変曲点になると想像できます。

Rによる正規分布とは

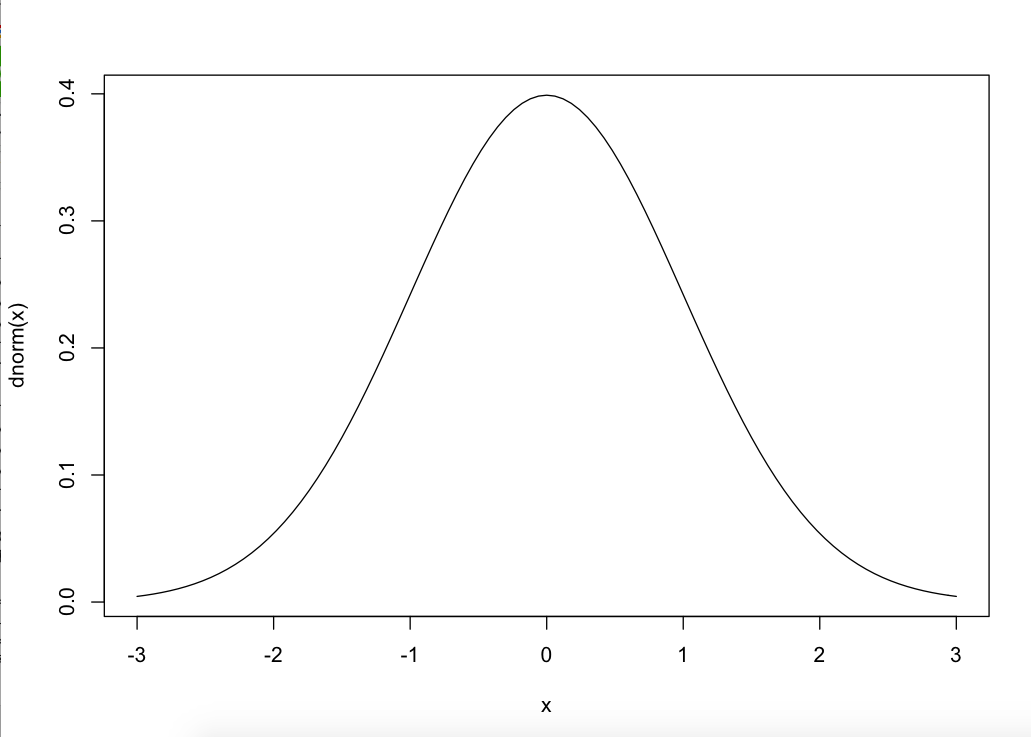
理屈だけではイメージできないので
可視化してみます。
平均0,分散1の正規分布は下記のようになります。

sample.R

> curve(dnorm,-3,3)

分散1と仮定してますので標準偏差は1となります。
x=±1でいい感じの変曲点になっているかと思います。

終わりに

なんとなく正規分布のグラフを書いてしまいがちですが、
高校数学を用いると多少正確に書けることができます。
（変曲点がどこなのか考えて描けます）

ちなみに
平均0分散1の正規分布を標準正規分布と呼びます。
また
平均50分散100（=標準偏差10）の正規分布は偏差値として使用されます。
（偏差値60の方は変曲点におります）

反省

私はネットサーファーですが、
実際に記事を書くと色々と苦労しました。
Qiitaを投稿している方々に改めて感謝しつつ、
私も有用なものをたくさん書きたいと思いました。