前編
この記事の続きです。
0.1の浮動小数点数は0.1より大きいのに、10回足すと1.0より小さいのはなぜか【前編】
(前編からのコピー)0.1を浮動小数点数で表すと
0.1を浮動小数点数で表したときの符号、指数、仮数は以下です。
符号 = 0
指数 = 01111111011
仮数 = 1001100110011001100110011001100110011001100110011010
指数を10進数で表すと1019です。浮動小数点形式の指数は1023が足されていますので、これを引くと-4になります。
(前編からのコピー)0.1を足していったときの結果とどのくらい足されているか
ヘッダを除いた奇数行に0.1を足していったときの計算結果、偶数行にそれぞれの差分は以下の表に示します。
| 期待値 | 計算結果/差分 |
|---|---|
| 0.1 | 0.1000000000000000055511151231257827021181583404541015625 |
0.1000000000000000055511151231257827021181583404541015625 |
|
| 0.2 | 0.200000000000000011102230246251565404236316680908203125 |
0.100000000000000033306690738754696212708950042724609375 |
|
| 0.3 | 0.3000000000000000444089209850062616169452667236328125 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 0.4 | 0.40000000000000002220446049250313080847263336181640625 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 0.5 | 0.5 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 0.6 | 0.59999999999999997779553950749686919152736663818359375 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 0.7 | 0.6999999999999999555910790149937383830547332763671875 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 0.8 | 0.79999999999999993338661852249060757458209991455078125 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 0.9 | 0.899999999999999911182158029987476766109466552734375 |
0.09999999999999997779553950749686919152736663818359375 |
|
| 1.0 | 0.99999999999999988897769753748434595763683319091796875 |
(前編からのコピー)浮動小数点数の足し算の手順
正の浮動小数点数同士の足し算は以下の手順で行われます。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
③ 仮数を足し合わせる
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
(前編からのコピー)保護桁とスティッキビット
保護桁(Guard digits)はあふれてしまった桁を保存する領域です。
スティッキビット(Sticky bit)は保護桁以下の数に1以上の数が含まれているかどうかを表す真偽値です。
前編で、正の数の加算では保護桁は1桁で十分という話が出ましたが、負の数まで拡張する場合は2桁必要です。
以下では保護桁2桁とスティッキッビットを使用します。保護桁の2桁(2bit)には、上からガードビット(Guard bit)、ラウンドビット(Round bit)という名前がついています。
0.1を10回足したときの計算過程
0.1を足したときの計算過程を順を追って確かめます。
今回使用する表現
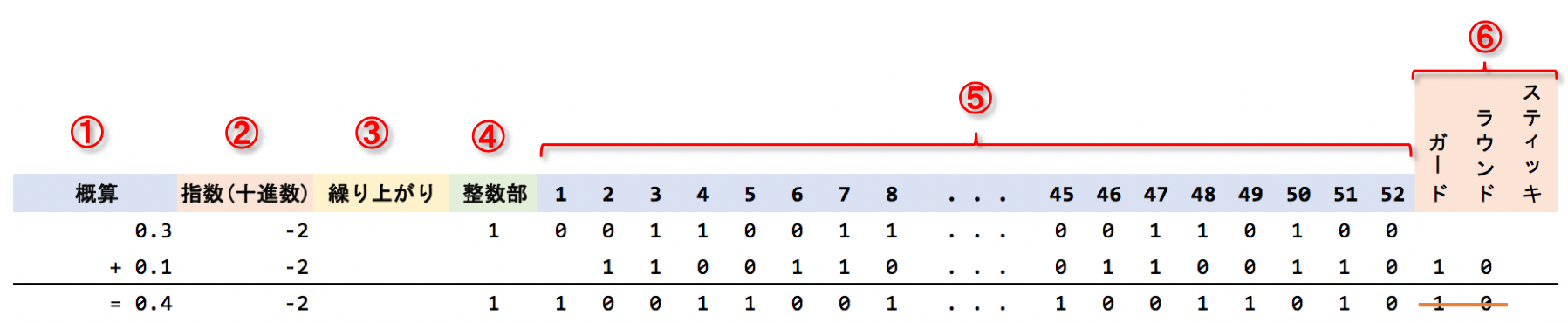
今回は以下のような図を用いて説明を行います。
| 番号 | 列名 | 説明 |
|---|---|---|
| ① | 概算 | どのような計算を行なっているのか大まかに記載しています。 |
| ② | 指数(十進数) | 浮動小数点数で表された指数を、10進数に変換し、1023を引いたものです。 |
| ③ | 繰り上がり | 足し算した結果、桁が繰り上がることがあるのでそのぶんの領域を確保しています。 |
| ④ | 整数部 | 浮動小数点形式では整数部は常に1です。 |
| ⑤ | 0から52 | 仮数です。52桁全部を表示するとみにくくなるため、上位8桁と下位8桁のみ表示しています。 |
| ⑥ | ガード・ラウンド・スティッキ | 上で説明した保護桁とスティッキビットです。 |
0.1 + 0.1 の計算過程
0.1 + 0.1の計算過程を確かめます。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
指数が同じなので何もしません。
③ 仮数を足し合わせる
足し合わせた結果です
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
繰り上げが発生しているので、指数に1を足し、仮数を2で割ります。2進数なので、2で割ると右に桁が1つずれます(ビットシフト)。
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
あふれたビットは0のみなので、切り捨てます。
以上で、
指数 = -3 (10進数)
仮数 = 1001100110011001100110011001100110011001100110011010 (2進数)
が得られました。これを10進数に変換すると、
0.200000000000000011102230246251565404236316680908203125
です。
0.2(累積和) + 0.1 の計算過程
上で得られた値にさらに0.1を足します。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
0.2の方が指数が1大きいので、0.1の指数に1を足し、仮数を1つ右にずらします
③ 仮数を足し合わせる
足し合わせた結果です。
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
繰り上げが発生しているので、指数に1を足し、仮数を右に1つずらします。
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
あふれてしまった桁は10で、半分ちょうどなので、偶数方向に丸めます。今回は仮数の最下位ビットが1なので、切り上げます。
以上で、
指数 = -2 (10進数)
仮数 = 11001100110011001100110011001100110011001100110100 (2進数)
が得られました。これを10進数に変換すると、
0.3000000000000000444089209850062616169452667236328125
です。
0.2(累積和) + 0.1では、もともと0.1が浮動小数点数では0.1より大きいことと、足した結果をさらに切り上げていることで、printしたときに期待したのとは違う結果が表示されます。
print(0.1 + 0.1 + 0.1)
# => 0.30000000000000004
0.3(累積和) + 0.1 の計算過程
上で得られた値にさらに0.1を足します。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
0.3の方が指数が2大きいので、0.1の指数に2を足し、仮数を2つ右にずらします。
③ 仮数を足し合わせる
足し合わせた結果です。
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
繰り上げは発生しなかったので、何もしません
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
あふれてしまった桁は10で、半分ちょうどなので、偶数方向に丸めます。今回は仮数の最下位ビットが0なので、切り捨てます。
以上で、
指数 = -2 (10進数)
仮数 = 1001100110011001100110011001100110011001100110011010 (2進数)
が得られました。これを10進数に変換すると、
0.40000000000000002220446049250313080847263336181640625
です。
0.4(累積和) + 0.1 の計算過程
上で得られた値にさらに0.1を足します。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
0.4の方が指数が2大きいので、0.1の指数に2を足し、仮数を2つ右にずらします。
③ 仮数を足し合わせる
足し合わせた結果です。仮数部のすべての値が0になりました。
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
繰り上げが発生しているので、指数に1を足し、仮数を1つ右にずらします。
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
あふれてしまった桁は010なので切り捨てられます。
以上で、
指数 = -1 (10進数)
仮数 = 0000000000000000000000000000000000000000000000000000 (2進数)
が得られました。これを10進数に直すと、
0.5
です。ぴったりになったのは偶然です。
0.5(累積和) + 0.1 の計算過程
上で得られた値にさらに0.1を足します。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
0.5の方が指数が3大きいので、0.1の指数に3を足し、仮数を3つ右にずらします。
③ 仮数を足し合わせる
足し合わせた結果です。
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
繰り上げは発生しなかったので、何もしません
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
あふれてしまった桁は010なので切り捨てられます。
以上で、
指数 = -1 (10進数)
仮数 = 11001100110011001100110011001100110011001100110011 (2進数)
が得られました。これを10進数に直すと、
0.59999999999999997779553950749686919152736663818359375
です。
0.6(累積和) + 0.1、0.7(累積和) + 0.1、0.8(累積和) + 0.1の計算過程
0.6から0.8までは0.5(累積和) + 0.1とほぼ同様なので省略します。値の切り捨てが発生するので、この範囲では1より小さい数が足されています。
0.9(累積和) + 0.1 の計算過程
こちらも0.5(累積和) + 0.1とほぼ同様ですが、結果がどのようになるかみてみましょう。
① 指数が小さい方を指数が大きい方に合わせる
② 指数を大きくしたぶん、仮数を小さくして調整する
0.9の方が指数が3大きいので、0.1の指数に3を足し、仮数を3つ右にずらします。
③ 仮数を足し合わせる
足し合わせた結果です。
④ 繰り上げが発生した場合は、指数に1を足しそのぶん仮数を小さくする
繰り上げは発生しなかったので、何もしません
⑤ 仮数のあふれてしまった桁を丸める(偶数丸め)
あふれてしまった桁は010なので切り捨てられます。
以上で、
指数 = -1 (10進数)
仮数 = 1111111111111111111111111111111111111111111111111111 (2進数)
が得られました。これを10進数に直すと、
0.99999999999999988897769753748434595763683319091796875
です。
ここまでで、0.1を10回足したときの動作を確認することができました。
まとめ
0.1を浮動小数点数にすると0.1よりわずかに大きくなるのに、10回足すと1.0より小さいのはなぜか、の答えは、
2つの浮動小数点数を足す際に、仮数に入りきらない数を丸めるから、でした。
参考資料
- 浮動小数点演算について
- 3.6 Floating Point(PDF)
- Why you need a Guard bit, in addition to the Round and Sticky bits(PDF)
- 浮動小数点の丸めの方向と性質 (1)
- decimal --- 十進固定及び浮動小数点数の算術演算